
Keplers Gesetzeserklärung, Übungen, Experimente
Das Keplers Gesetze über Planetenbewegungen wurden vom deutschen Astronomen Johannes Kepler (1571-1630) formuliert. Kepler folgerte sie aufgrund der Arbeit seines Lehrers, des dänischen Astronomen Tycho Brahe (1546-1601)..
Brahe stellte sorgfältig Daten über Planetenbewegungen über mehr als 20 Jahre mit überraschender Präzision und Genauigkeit zusammen, da das Teleskop zu diesem Zeitpunkt noch nicht erfunden worden war. Die Gültigkeit Ihrer Daten gilt noch heute.

Artikelverzeichnis
- 1 Keplers 3 Gesetze
- 2 Das Gesetz der universellen Gravitation und Keplers drittes Gesetz
- 3 Übungen
- 3.1 - Übung 1
- 3.2 - Übung 2
- 4 experimentieren
- 4.1 Materialien
- 4.2 Vorgehensweise
- 5 Referenzen
Keplers 3 Gesetze
Keplers Gesetze besagen:
-Erstes Gesetz: Alle Planeten beschreiben elliptische Bahnen mit der Sonne in einem der Brennpunkte.
-Zweites Gesetz oder Gesetz gleicher Bereiche: Eine Linie, die von der Sonne zu einem beliebigen Planeten (Brennradius) gerichtet ist, fegt gleiche Flächen zu gleichen Zeiten.
-Drittes Gesetz: Das Quadrat der Zeit, die ein Planet benötigt, um die Sonne zu umkreisen, ist proportional zum Würfel seiner durchschnittlichen Entfernung von der Sonne.
Sein T. sagte Zeit, angerufen Umlaufzeit, Y. r die durchschnittliche Entfernung, dann:
T.zwei ist proportional zu r3
T = k r3
Dies bedeutet, dass der Quotient T.zwei/ r3 ist für alle Planeten gleich, was es ermöglicht, den Orbitalradius zu berechnen, wenn die Orbitalperiode bekannt ist.
Wann T. wird in Jahren und ausgedrückt r in astronomischen Einheiten AU * beträgt die Proportionalitätskonstante k = 1:
T.zwei= r3
* Eine astronomische Einheit entspricht 150 Millionen Kilometern, was der durchschnittlichen Entfernung zwischen der Erde und der Sonne entspricht. Die Umlaufzeit der Erde beträgt 1 Jahr.
Das Gesetz der universellen Gravitation und Keplers drittes Gesetz
Das universelle Gravitationsgesetz besagt, dass die Größe der Gravitationsanziehungskraft zwischen zwei Massenobjekten M. Y. m jeweils, deren Zentren durch einen Abstand voneinander getrennt sind r, ist gegeben durch:
F = G mM / rzwei
G ist die universelle Gravitationskonstante und ihr Wert ist G = 6,674 x 10 -elf N.m.zwei/ kgzwei .
Jetzt sind die Umlaufbahnen der Planeten elliptisch mit einer sehr kleinen Exzentrizität.
Dies bedeutet, dass die Umlaufbahn nicht sehr weit von einem Umfang entfernt ist, außer in einigen Fällen wie dem Zwergplaneten Pluto. Wenn wir die Umlaufbahnen der Kreisform annähern, beträgt die Beschleunigung der Bewegung des Planeten:
zuc = vzwei/ r
Angenommen F = ma, haben:
G mM / rzwei = m.v.zwei/ r
Hier v ist die lineare Geschwindigkeit des Planeten um die Sonne, angenommen statisch und von Masse M., während das des Planeten ist m. Dann:

Dies erklärt, dass die Planeten, die weiter von der Sonne entfernt sind, eine geringere Umlaufgeschwindigkeit haben, da dies davon abhängt 1 / √r.
Da die Entfernung, die der Planet zurücklegt, ungefähr der Länge des Umfangs entspricht: L = 2πr und es eine Zeit dauert, die T, der Umlaufzeit, entspricht, erhalten wir:
v = 2πr / T.
Das Gleichsetzen beider Ausdrücke für v ergibt einen gültigen Ausdruck für T.zwei, das Quadrat der Umlaufzeit:

Und dies ist genau Keplers drittes Gesetz, da in diesem Ausdruck die Klammer steht 4πzwei / GM ist daher konstant T.zwei ist proportional zur Entfernung r gewürfelt.
Die endgültige Gleichung für die Umlaufzeit ergibt sich aus der Quadratwurzel:

Wie viel ist die Masse der Sonne wert? Es ist möglich, durch diese Gleichung herauszufinden. Wir wissen, dass die Umlaufzeit der Erde ein Jahr beträgt und der Umlaufradius 1 AE entspricht, was 150 Millionen Kilometern entspricht. Wir haben also alle erforderlichen Daten.
In unserer vorherigen Gleichung lösen wir nach M., nicht ohne vorher alle Werte in das Internationale Einheitensystem SI umzurechnen:
1 Jahr = 3,16 x 107 Sekunden.
1 AU = 150 Millionen km = 1,5 x 10elf m.

Ausbildung
Obwohl Kepler nur die Planeten im Auge hatte, als er seine berühmten Gesetze ableitete, gelten diese auch für die Bewegung von Satelliten und anderen Körpern im Sonnensystem, wie wir weiter unten sehen werden..
- Übung 1
Wenn Sie wissen, dass die Umlaufbahn des Jupiter 5,19-mal so groß ist wie die der Erde, finden Sie die Umlaufzeit des Jupiter.
Lösung
Nach der Definition der Astronomischen Einheit ist Jupiter von der Sonne entfernt. 5.19 AU, daher nach Keplers drittem Gesetz:
T.zwei= r3= (5,19)3 Jahre
Deshalb T = (5,19)3/2 Jahre = 11,8 Jahre
- Übung 2
Der Komet Halley besucht die Sonne alle 75,3 Jahre. Finden:
a) Die Semi-Major-Achse ihrer Umlaufbahn.
b) Das Aphelmaß, wenn das Perihel 0,568 AU misst.
Lösung
Der Komet Halley besucht die Sonne alle 75,3 Jahre. Finden:
a) Die Semi-Major-Achse ihrer Umlaufbahn.
b) Das Aphelion-Maß, wenn das Perihel 0,568 AU misst.
Lösung für
Wenn sich ein Planet oder ein anderer Stern an seinem der Sonne am nächsten gelegenen Punkt befindet, wird er als in der Sonne befindlich bezeichnet Perihel, und wenn es weiter weg ist, in Aphel. Im speziellen Fall einer Kreisbahn ist r in Keplers drittem Gesetz der Radius der Bahn.
In der elliptischen Umlaufbahn ist der Himmelskörper jedoch mehr oder weniger weit von der Sonne entfernt, wobei die Semi-Major-Achse "a" der Durchschnitt zwischen Aphel und Perihel ist:

Daher ersetzen wir in Keplers drittem Gesetz a durch r, was für Halley Folgendes ergibt:
T.zwei= a3→ a = (T)2/3 → a = (75,3) 2/3 UA = 17.832 UA
Lösung b
a = ½ (Perihel + Aphel)
17,832 = ½ (0,568+ Aphel) → Aphel = 2 × 17,832 - 0,568 AU = 35,10 AU.
Experiment
Die Analyse der Bewegung der Planeten erfordert Wochen, Monate und sogar Jahre sorgfältiger Beobachtung und Aufzeichnung. Im Labor kann jedoch ein sehr einfaches Skalenexperiment durchgeführt werden, um zu beweisen, dass Keplers Gesetz der gleichen Flächen gilt..
Hierzu ist ein physikalisches System erforderlich, in dem die die Bewegung regierende Kraft zentral ist, eine ausreichende Voraussetzung für die Erfüllung des Gebietsgesetzes. Ein solches System besteht aus einer Masse, die an ein langes Seil gebunden ist, wobei das andere Ende des Gewindes an einem Träger befestigt ist..
Die Masse wird um einen kleinen Winkel von ihrer Gleichgewichtsposition bewegt und mit einem leichten Impuls versehen, so dass sie eine ovale (fast elliptische) Bewegung in der horizontalen Ebene ausführt, als wäre sie ein Planet um die Sonne..
Auf der vom Pendel beschriebenen Kurve können wir beweisen, dass es gleiche Flächen zu gleichen Zeiten fegt, wenn:
-Wir betrachten Vektorradien, die vom Anziehungspunkt (Anfangspunkt des Gleichgewichts) zur Position der Masse gehen.
-Und wir wechseln zwischen zwei aufeinanderfolgenden Momenten gleicher Dauer in zwei verschiedenen Bereichen der Bewegung.
Je länger die Pendelschnur und je kleiner der Winkel von der Vertikalen entfernt ist, desto horizontaler ist die Nettowiederherstellungskraft und die Simulation ähnelt dem Fall einer Bewegung mit zentraler Kraft in einer Ebene.
Dann nähert sich das beschriebene Oval einer Ellipse, wie der, auf der sich die Planeten bewegen.
Materialien
-Nicht dehnbarer Faden
-1 Teig oder Metallkugel weiß lackiert, die als Pendelspule fungiert
-Herrscher
-Förderer
-Fotokamera mit automatischer Blitzscheibe
-Klammern
-Zwei Lichtquellen
-Ein Blatt schwarzes Papier oder Pappe
Prozess
Das Zusammenbauen der Figur ist erforderlich, um Fotos von mehreren Blitzen des Pendels zu machen, wenn es seinem Weg folgt. Dazu müssen Sie die Kamera direkt über dem Pendel und der automatischen Blitzscheibe vor dem Objektiv platzieren.
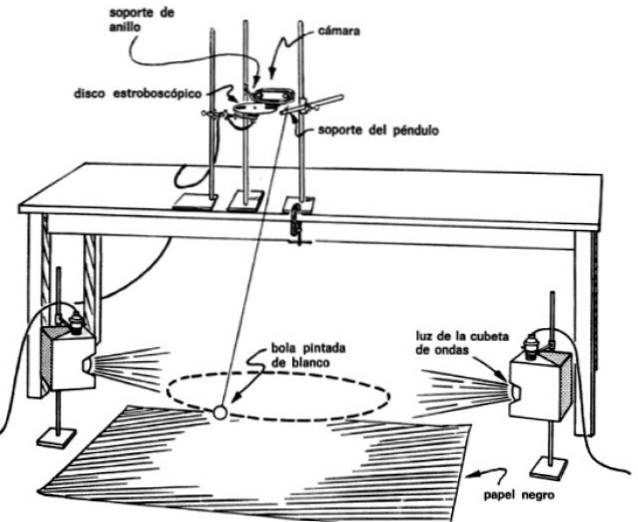
Auf diese Weise werden Bilder in regelmäßigen Zeitintervallen des Pendels erhalten, beispielsweise alle 0,1 oder alle 0,2 Sekunden, wodurch die Zeit ermittelt werden kann, die für die Bewegung von einem Punkt zum anderen benötigt wurde..
Sie müssen auch die Masse des Pendels richtig beleuchten und die Lichter auf beiden Seiten platzieren. Die Linse sollte weiß gestrichen werden, um den Kontrast auf dem Hintergrund zu verbessern, der aus einem schwarzen Papier besteht, das auf dem Boden verteilt ist.
Jetzt müssen Sie überprüfen, ob das Pendel gleiche Flächen zu gleichen Zeiten fegt. Dazu wird ein Zeitintervall gewählt und die vom Pendel in diesem Intervall eingenommenen Punkte auf dem Papier markiert..
Auf dem Bild wird eine Linie von der Mitte des Ovals zu diesen Punkten gezogen, und somit wird der erste der Bereiche vom Pendel überstrichen, bei dem es sich ungefähr um einen elliptischen Sektor wie den unten gezeigten handelt:
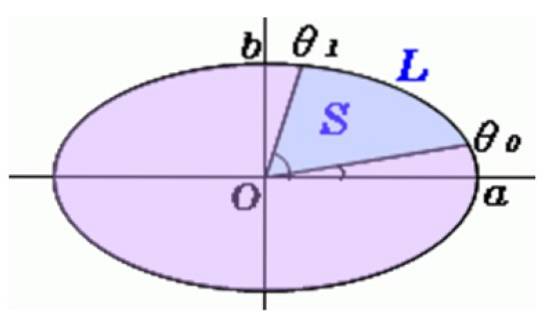
Berechnung der Fläche des elliptischen Abschnitts
Winkel werden mit dem Winkelmesser gemessen θoder Y. θ1, und diese Formel wird verwendet, um S, den Bereich des elliptischen Sektors, zu finden:
S = F (θ1) - F (θoder)
Mit F (θ) gegeben durch:

Beachten Sie, dass zu Y. b sind die Halb-Haupt- und Nebenachse. Der Leser muss sich nur um die sorgfältige Messung der Halbachsen und der Winkel kümmern, da online Taschenrechner verfügbar sind, mit denen dieser Ausdruck leicht ausgewertet werden kann..
Wenn Sie jedoch darauf bestehen, die Berechnung von Hand durchzuführen, denken Sie daran, dass der Winkel θ in Grad gemessen wird. Bei der Eingabe der Daten in den Taschenrechner müssen die Werte jedoch im Bogenmaß angegeben werden.
Dann müssen Sie ein weiteres Punktpaar markieren, bei dem das Pendel das gleiche Zeitintervall invertiert hat, und den entsprechenden Bereich zeichnen und seinen Wert mit dem gleichen Verfahren berechnen.
Überprüfung des Gesetzes gleicher Flächen
Schließlich muss noch überprüft werden, ob das Gesetz der Gebiete erfüllt ist, dh ob gleiche Gebiete zu gleichen Zeiten gefegt werden.
Weichen die Ergebnisse etwas von den Erwartungen ab? Es ist immer zu beachten, dass alle Messungen von ihrem jeweiligen experimentellen Fehler begleitet werden.
Verweise
- Keisan Online-Rechner. Fläche eines elliptischen Sektorrechners. Wiederhergestellt von: keisan.casio.com.
- Openstax. Keplers Gesetz der Planetenbewegung. Wiederhergestellt von: openstax.org.
- PSSC. Laborphysik. Editorial Reverté. Wiederhergestellt von: books.google.co.
- Palen, S. 2002. Astronomie. Schaum-Serie. Mcgraw Hügel.
- Pérez R. Einfaches System mit zentraler Kraft. Wiederhergestellt von: francesphysics.blogspot.com
- Stern, D. Keplers drei Gesetze der Planetenbewegung. Wiederhergestellt von: phy6.org.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.