Das Gesetz für Hardy-Weinberg, Es wird auch als Hardy-Weinberg-Prinzip oder Gleichgewicht bezeichnet und besteht aus einem mathematischen Theorem, das eine hypothetische diploide Population mit sich nicht entwickelnder sexueller Reproduktion beschreibt - die Allelfrequenzen ändern sich nicht von Generation zu Generation.
Dieses Prinzip setzt fünf Bedingungen voraus, die erforderlich sind, damit die Population konstant bleibt: Fehlen eines Genflusses, Fehlen von Mutationen, zufällige Paarung, Fehlen einer natürlichen Selektion und eine unendlich große Populationsgröße. Auf diese Weise bleibt die Bevölkerung ohne diese Kräfte im Gleichgewicht.
Wenn eine der oben genannten Annahmen nicht erfüllt ist, tritt eine Änderung auf. Aus diesem Grund sind natürliche Selektion, Mutation, Migration und genetische Drift die vier Evolutionsmechanismen..
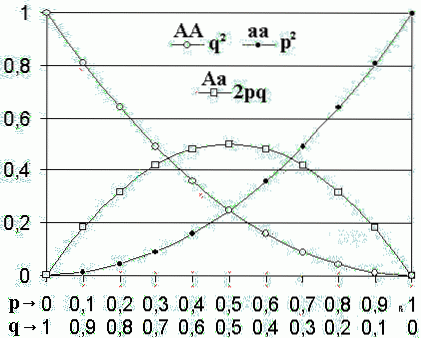
Nach diesem Modell, wenn die Allelfrequenzen einer Population sind p Y. Was, Genotypfrequenzen werden sein pzwei, zweipq Y. Waszwei.
Wir können das Hardy-Weinberg-Gleichgewicht bei der Berechnung der Häufigkeit bestimmter interessierender Allele anwenden, um beispielsweise den Anteil von Heterozygoten in einer menschlichen Bevölkerung abzuschätzen. Wir können auch überprüfen, ob sich eine Bevölkerung im Gleichgewicht befindet oder nicht, und Hypothesen vorschlagen, dass Kräfte auf diese Bevölkerung wirken..
Artikelverzeichnis
Das Hardy-Weinberg-Prinzip wurde 1908 geboren und verdankt seinen Namen seinen Wissenschaftlern G.H. Hardy und W. Weinberg, die unabhängig voneinander zu den gleichen Ergebnissen kamen.
Zuvor hatte ein anderer Biologe namens Udny Yule das Problem 1902 angegangen. Yule begann mit einer Reihe von Genen, bei denen die Häufigkeit beider Allele 0,5 und 0,5 betrug. Der Biologe zeigte, dass die Frequenzen während der folgenden Generationen beibehalten wurden.
Obwohl Yule zu dem Schluss kam, dass die Allelfrequenzen stabil gehalten werden könnten, war seine Interpretation zu wörtlich. Er glaubte, dass der einzige Gleichgewichtszustand gefunden wurde, wenn die Frequenzen dem Wert von 0,5 entsprachen.
Yule diskutierte hitzig ihre neuartigen Erkenntnisse mit R.C. Punnett - weithin bekannt auf dem Gebiet der Genetik für die Erfindung des berühmten "Punnett-Platzes". Obwohl Punnett wusste, dass Yule falsch lag, fand er keinen mathematischen Weg, dies zu beweisen..
Daher kontaktierte Punnett seinen Mathematiker-Freund Hardy, der es sofort schaffte, es zu lösen, indem er die Berechnungen unter Verwendung allgemeiner Variablen wiederholte und nicht den festen Wert von 0,5, wie Yule es getan hatte..
Die Populationsgenetik zielt darauf ab, die Kräfte zu untersuchen, die zu Veränderungen der Allelfrequenzen in Populationen führen, und Charles Darwins Evolutionstheorie durch natürliche Selektion und Mendelsche Genetik zu integrieren. Heute bilden seine Prinzipien die theoretische Grundlage für das Verständnis vieler Aspekte der Evolutionsbiologie..
Eine der entscheidenden Ideen der Populationsgenetik ist die Beziehung zwischen Änderungen der relativen Häufigkeit von Merkmalen und Änderungen der relativen Häufigkeit der Allele, die sie regulieren, erklärt durch das Hardy-Weinberg-Prinzip. Tatsächlich liefert dieser Satz den konzeptionellen Rahmen für die Populationsgenetik..
Im Lichte der Populationsgenetik lautet das Konzept der Evolution wie folgt: Veränderung der Allelfrequenzen über Generationen. Wenn es keine Veränderung gibt, gibt es keine Evolution.
Das Hardy-Weinberg-Gleichgewicht ist ein Nullmodell, mit dem wir das Verhalten von Gen- und Allelfrequenzen über Generationen hinweg spezifizieren können. Mit anderen Worten, es ist das Modell, das das Verhalten von Genen in Populationen unter einer Reihe spezifischer Bedingungen beschreibt..
Im Hardy-Weinbergm-Theorem ist die Allelfrequenz von ZU (dominantes Allel) wird durch den Buchstaben dargestellt p, während die Allelfrequenz von zu (rezessives Allel) wird durch den Buchstaben dargestellt Was.
Die erwarteten Genotypfrequenzen sind pzwei, zweipq Y. Waszwei, für die homozygote Dominante (AA), heterozygot (Aa) und homozygot rezessiv (aa), beziehungsweise.
Wenn sich an diesem Ort nur zwei Allele befinden, muss die Summe der Frequenzen der beiden Allele notwendigerweise gleich 1 sein (p + q = 1). Die Binomialerweiterung (p + q)zwei Genotypfrequenzen darstellen pzwei + zweipq + qzwei = 1.
In einer Population kreuzen sich die Individuen, aus denen es besteht, um Nachkommen hervorzubringen. Im Allgemeinen können wir auf die wichtigsten Aspekte dieses Fortpflanzungszyklus hinweisen: die Produktion von Gameten, ihre Fusion zur Entstehung einer Zygote und die Entwicklung des Embryos zur Entstehung der neuen Generation..
Stellen Sie sich vor, wir können den Mendelschen Genprozess in den genannten Ereignissen verfolgen. Wir tun dies, weil wir wissen wollen, ob und warum die Häufigkeit eines Allels oder Genotyps zunimmt oder abnimmt..
Um zu verstehen, wie sich die Gen- und Allelfrequenzen in einer Population unterscheiden, werden wir die Gametenproduktion einer Gruppe von Mäusen verfolgen. In unserem hypothetischen Beispiel erfolgt die Paarung zufällig, wobei alle Spermien und Eier zufällig gemischt werden..
Bei Mäusen trifft diese Annahme nicht zu und ist nur eine Vereinfachung, um die Berechnungen zu erleichtern. In einigen Tiergruppen, wie bestimmten Stachelhäutern und anderen Wasserorganismen, werden Gameten jedoch ausgestoßen und kollidieren zufällig..
Konzentrieren wir uns nun auf einen bestimmten Ort mit zwei Allelen: ZU Y. zu. Nach dem von Gregor Mendel verkündeten Gesetz erhält jeder Gamet ein Allel vom Ort A. Angenommen, 60% der Eizellen und Spermien erhalten das Allel ZU, während die restlichen 40% das Allel erhielten zu.
Daher die Allelfrequenz ZU ist 0,6 und das des Allels zu ist 0,4. Diese Gruppe von Gameten wird zufällig gefunden, um eine Zygote hervorzurufen. Wie hoch ist die Wahrscheinlichkeit, dass sie jeden der drei möglichen Genotypen bilden? Dazu müssen wir die Wahrscheinlichkeiten wie folgt multiplizieren:
Genotyp AA: 0,6 x 0,6 = 0,36.
Genotyp Aa: 0,6 x 0,4 = 0,24. Im Fall der Heterozygote gibt es zwei Formen, aus denen sie stammen kann. Das erste, dass das Sperma das Allel trägt ZU und die Eizelle das Allel zu, oder im umgekehrten Fall das Sperma der zu und die Eizelle ZU. Deshalb addieren wir 0,24 + 0,24 = 0,48.
Genotyp aa: 0,4 x 0,4 = 0,16.
Stellen wir uns nun vor, dass sich diese Zygoten entwickeln und zu erwachsenen Mäusen werden, die wieder Gameten produzieren. Würden wir erwarten, dass die Allelfrequenzen gleich oder verschieden von der vorherigen Generation sind??
Genotyp AA wird 36% der Gameten produzieren, während Heterozygoten 48% der Gameten und den Genotyp produzieren werden aa 16%.
Um die neue Allelfrequenz zu berechnen, addieren wir die Frequenz des Homozygoten plus die Hälfte des Heterozygoten wie folgt:
Allelfrequenz ZU: 0,36 + ½ (0,48) = 0,6.
Allelfrequenz zu: 0,16 + ½ (0,48) = 0,4.
Wenn wir sie mit den Anfangsfrequenzen vergleichen, werden wir feststellen, dass sie identisch sind. Nach dem Konzept der Evolution befindet sich die Population daher im Gleichgewicht, da sich die Allelfrequenzen über Generationen hinweg nicht ändern - sie entwickelt sich nicht..
Welche Bedingungen muss die vorherige Population erfüllen, damit ihre Allelfrequenzen über die Generationen hinweg konstant bleiben? Im Hardy-Weinberg-Gleichgewichtsmodell erfüllt die sich nicht entwickelnde Population die folgenden Annahmen:
Die Population muss extrem groß sein, um stochastische oder zufällige Auswirkungen der Gendrift zu vermeiden.
Wenn die Populationen klein sind, ist der Effekt der Gendrift (zufällige Änderungen der Allelfrequenzen von einer Generation zur anderen) aufgrund von Stichprobenfehlern viel größer und kann zur Fixierung oder zum Verlust bestimmter Allele führen..
Migrationen gibt es in der Bevölkerung nicht, so dass Allele, die die Genfrequenzen verändern können, nicht ankommen oder gehen können.
Mutationen sind Veränderungen in der DNA-Sequenz und können unterschiedliche Ursachen haben. Diese zufälligen Veränderungen modifizieren den Genpool in der Population durch die Einführung oder Eliminierung von Genen in den Chromosomen.
Das Mischen der Gameten muss zufällig erfolgen - wie die Annahme, die wir im Mausbeispiel verwendet haben. Daher sollte es unter den Individuen in der Bevölkerung keine Partnerwahl geben, einschließlich Inzucht (Reproduktion verwandter Individuen)..
Wenn die Paarung nicht zufällig ist, verursacht sie keine Änderung der Allelfrequenzen von einer Generation zur nächsten, kann jedoch Abweichungen von den erwarteten Genotypfrequenzen erzeugen..
Es gibt keinen unterschiedlichen Fortpflanzungserfolg von Personen mit unterschiedlichen Genotypen, die die Allelfrequenzen in der Bevölkerung verändern können..
Mit anderen Worten, in der hypothetischen Population haben alle Genotypen die gleiche Wahrscheinlichkeit, sich zu reproduzieren und zu überleben..
Wenn eine Bevölkerung diese fünf Bedingungen nicht erfüllt, ist das Ergebnis die Evolution. Logischerweise erfüllen natürliche Populationen diese Annahmen nicht. Daher wird das Hardy-Weinberg-Modell als Nullhypothese verwendet, die es uns ermöglicht, ungefähre Schätzungen der Gen- und Allelfrequenzen vorzunehmen..
Neben dem Fehlen dieser fünf Bedingungen gibt es andere mögliche Ursachen, warum sich die Bevölkerung nicht im Gleichgewicht befindet.
Eine davon tritt auf, wenn loci sind mit Geschlechts- oder Verzerrungsphänomenen in der Segregation verbunden oder meiotischer Antrieb (wenn nicht jede Kopie eines Gens oder Chromosoms mit gleicher Wahrscheinlichkeit an die nächste Generation übertragen wird).
In den Vereinigten Staaten leidet schätzungsweise eines von 10.000 Neugeborenen an einer als Phenylketonurie bezeichneten Erkrankung..
Diese Störung wird nur in rezessiven Homozygoten bei einer Stoffwechselstörung exprimiert. Wie häufig sind Träger der Krankheit in der Bevölkerung, wenn man diese Daten kennt??
Um die Hardy-Weinberg-Gleichung anzuwenden, müssen wir davon ausgehen, dass die Wahl des Partners nicht mit dem mit der Pathologie verbundenen Gen zusammenhängt und es keine Inzucht gibt.
Darüber hinaus gehen wir davon aus, dass es in den USA keine Migrationsphänomene gibt, dass es keine neuen Phenylketonurie-Mutationen gibt und dass die Wahrscheinlichkeit der Reproduktion und des Überlebens zwischen den Genotypen gleich ist..
Wenn die oben genannten Bedingungen zutreffen, können wir die Hardy-Weinberg-Gleichung verwenden, um für das Problem relevante Berechnungen durchzuführen..
Wir wissen, dass es alle 10.000 Geburten einen Fall der Krankheit gibt Waszwei = 0,0001 und die Häufigkeit des rezessiven Allels ist die Quadratwurzel dieses Wertes: 0,01.
Was p = 1 - Was, wir müssen p beträgt 0,99. Jetzt haben wir die Häufigkeit beider Allele: 0,01 und 0,99. Die Trägerfrequenz bezieht sich auf die Häufigkeit von Heterozygoten, die als 2 berechnet wirdpq. Somit ist 2pq = 2 × 0,99 × 0,01 = 0,0198.
Dies entspricht ungefähr 2% der Bevölkerung. Denken Sie daran, dass dies nur ein ungefähres Ergebnis ist.
Wenn wir die Anzahl jedes Genotyps in der Population kennen, können wir schließen, ob er sich im Hardy-Weinberg-Gleichgewicht befindet. Die Schritte zur Lösung dieser Art von Problemen sind wie folgt:
p = D. + ½ H.
q = R. + ½ H.
Zum Beispiel möchten wir überprüfen, ob sich die folgende Schmetterlingspopulation im Hardy-Weinberg-Gleichgewicht befindet: Es gibt 79 Individuen mit homozygot dominantem Genotyp (AA), 138 der Heterozygote (Aa) und 61 der homozygoten rezessiven (aa).
Der erste Schritt besteht darin, die beobachteten Frequenzen zu berechnen. Dazu dividieren wir die Anzahl der Individuen pro Genotyp durch die Gesamtzahl der Individuen:
D = 79/278 = 0,28
H = 138/278 = 0,50
R = 61/278 = 0,22
Um zu überprüfen, ob ich es gut gemacht habe, ist der erste Schritt, ich füge alle Frequenzen hinzu und es sollte 1 ergeben.
Der zweite Schritt ist die Berechnung der Allelfrequenzen.
p = 0,28 + ½ (0,50) = 0,53
Was = 0,22 + ½ (0,50) = 0,47
Mit diesen Daten kann ich die erwarteten Genotypfrequenzen berechnen (pzwei, zweiwarum und waszwei)
pzwei = 0,28
zweipq = 0,50
Waszwei = 0,22
Ich berechne die erwarteten Zahlen und multipliziere die erwarteten Häufigkeiten mit der Anzahl der Personen. In diesem Fall ist die Anzahl der beobachteten und erwarteten Personen identisch, sodass ich den Schluss ziehen kann, dass sich die Bevölkerung im Gleichgewicht befindet.
Wenn die erhaltenen Zahlen nicht identisch sind, muss ich den genannten statistischen Test anwenden (X.zwei von Pearson).
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.