Heptadecagon-Eigenschaften, Diagonalen, Umfang, Fläche

Das Siebeneck ist ein reguläres Polygon mit 17 Seiten und 17 Eckpunkten. Seine Konstruktion kann im euklidischen Stil erfolgen, dh nur mit dem Lineal und dem Kompass. Es war das große mathematische Genie Carl Friedrich Gauss (1777-1855), kaum 18 Jahre alt, das 1796 das Verfahren für seinen Bau fand. 

Anscheinend neigte Gauß immer sehr zu dieser geometrischen Figur, so dass er sich von dem Tag an, an dem er ihre Konstruktion entdeckte, entschied, Mathematiker zu werden. Es wird auch gesagt, dass er wollte, dass das Siebeneck in seinen Grabstein eingraviert wird.

Gauß fand auch die Formel, um zu bestimmen, welche regulären Polygone die Möglichkeit haben, mit Lineal und Kompass konstruiert zu werden, da einige keine exakte euklidische Konstruktion haben.

Artikelverzeichnis

• 1 Eigenschaften des Heptadecagons
• 2 Diagonalen und Umfang
  • 2.1 Umfang des Heptadecagons 
• 3 Bereich
  • 3.1 Fläche auf der Seite gegeben
  • 3.2 Fläche unter Berücksichtigung des Radius
• 4 Beispiele
  • 4.1 Beispiel 1
  • 4.2 Beispiel 2
• 5 Referenzen

Eigenschaften des Heptadecagons

Wie bei jedem Polygon ist auch bei seinen Eigenschaften die Summe seiner Innenwinkel wichtig. In einem regelmäßigen Polygon von n Seiten ist die Summe gegeben durch:

Sa (n) = (n - 2) * 180º.

Für das Siebeneck die Anzahl der Seiten n es ist 17, was bedeutet, dass die Summe seiner Innenwinkel ist:

Sa (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Diese Summe, ausgedrückt im Bogenmaß, sieht folgendermaßen aus:

Sa (17) = (17-2) * π = 15 * π = 15π

Aus den obigen Formeln kann leicht abgeleitet werden, dass jeder Innenwinkel eines Heptadecagons ein genaues Maß α hat, das gegeben ist durch:

α = 2700º / 17 = (15/17) π Bogenmaß

Daraus folgt, dass der Innenwinkel in ungefährer Form ist:

α ≈ 158.824º

Diagonalen und Umfang

Diagonalen und Umfang sind weitere wichtige Aspekte. In jedem Polygon beträgt die Anzahl der Diagonalen: 

D = n (n - 3) / 2 und im Fall des Siebeneckens als n = 17, es ist dann das D = 119 Diagonalen.

Wenn andererseits die Länge jeder Seite des Heptadecagon bekannt ist, wird der Umfang des regulären Heptadecagon einfach durch Hinzufügen der 17-fachen Länge oder der 17-fachen Länge ermittelt d Auf jeder Seite:

P = 17 d

Umfang des Siebenecks 

Manchmal ist nur der Radius bekannt r des Heptadecagon, so ist es notwendig, eine Formel für diesen Fall zu entwickeln.

Zu diesem Zweck ist das Konzept von Apothema. Das Apothem ist das Segment, das von der Mitte des regulären Polygons zum Mittelpunkt einer Seite verläuft. Das Apothem relativ zu einer Seite ist senkrecht zu dieser Seite (siehe Abbildung 2).

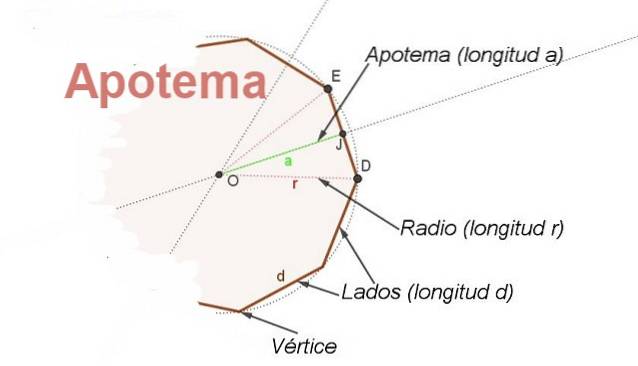
Darüber hinaus ist das Apothem die Winkelhalbierende mit dem zentralen Scheitelpunkt und den Seiten an zwei aufeinanderfolgenden Scheitelpunkten des Polygons. Dadurch kann eine Beziehung zwischen dem Radius gefunden werden r und die Seite d.

Wenn es heißt β zum zentralen Winkel DAMHIRSCHKUH und unter Berücksichtigung, dass das Apothem ABl ist die Halbierende, die du hast EJ = d / 2 = r Sen (β / 2), von wo gibt es eine Beziehung, um die Länge zu finden d auf der Seite eines bekannten Polygons seinen Radius r und sein zentraler Winkel β::

d = 2 r Sen (β / 2)

Im Fall des Heptadecagons β = 360º / 17 Also hast du:

d = 2 r Sen (180º / 17) ≤ 0,3675 r

Schließlich wird die Formel für den Umfang des Heptadecagons erhalten, dessen Radius bekannt ist:

P = 34 r Sen (180º / 17) ≤ 6,2475 r

Der Umfang eines Heptadecagons liegt nahe am Umfang des Umfangs, der es umgibt, aber sein Wert ist kleiner, dh der Umfang des umschriebenen Kreises ist Pcir = 2π r ≤ 6,2832 r.

Bereich

Um die Fläche des Heptadecagons zu bestimmen, beziehen wir uns auf Abbildung 2, die die Seiten und das Apothem eines regelmäßigen Polygons von zeigt n Seiten. In dieser Figur das Dreieck EOD hat eine Fläche gleich der Basis d (Polygonseite) mal Höhe zu (Polygon apothem) dividieren durch zwei::

EOD-Fläche = (d x a) / 2

So bekannt das Apothem zu des Heptadecagon und der Seite d seine Fläche ist:

Heptadecagon-Fläche = (17/2) (d x a)

Fläche gegeben die Seite

Um eine Formel für die Fläche des Heptadecagons zu erhalten, die die Länge seiner siebzehn Seiten kennt, ist es notwendig, eine Beziehung zwischen der Länge des Apothems zu erhalten zu und die Seite d.

Unter Bezugnahme auf 2 wird die folgende trigonometrische Beziehung erhalten:

Tan (β / 2) = EJ / OJ = (d / 2) / a, Sein β zum zentralen Winkel DAMHIRSCHKUH. Also das Apothem zu kann berechnet werden, wenn die Länge bekannt ist d von der Seite des Polygons und dem Mittelwinkel β::

a = (d / 2) Cotan (β / 2)

Wenn dieser Ausdruck nun das Apothem ersetzt, haben wir in der Formel für die Fläche des Heptadecagons, die im vorherigen Abschnitt erhalten wurde, Folgendes:

Heptadecagon-Bereich = (17/4) (d^zwei) Cotan (β / 2)

Sein β = 360º / 17 für das Heptadecagon haben wir also endlich die gewünschte Formel:

Heptadecagon-Bereich = (17/4) (d^zwei) Cotan (180º / 17)

Fläche unter Angabe des Radius

In den vorhergehenden Abschnitten wurde eine Beziehung zwischen der Seite d eines regulären Polygons und seinem Radius r gefunden, wobei diese Beziehung die folgende ist:

d = 2 r Sen (β / 2)

Dieser Ausdruck für d wird in den Ausdruck eingeführt, der im vorherigen Abschnitt für den Bereich erhalten wurde. Wenn die entsprechenden Substitutionen und Vereinfachungen vorgenommen werden, wird die Formel erhalten, mit der die Fläche des Heptadecagons berechnet werden kann:

Heptadecagon-Bereich = (17/2) (r^zwei) Sen (β) = (17/2) (r^zwei) Sen (360º / 17)

Ein ungefährer Ausdruck für das Gebiet ist:

Heptadecagon-Fläche = 3,0706 (r^zwei) 

Wie erwartet ist dieser Bereich etwas kleiner als der Bereich des Kreises, der das Siebeneck umschreibt. ZU_circ = π r^zwei ≈ 3.1416 r^zwei. Um genau zu sein, ist es 2% weniger als das seines umschriebenen Kreises.

Beispiele

Beispiel 1

Welchen Wert müssen Radius und Durchmesser des umschriebenen Umfangs haben, damit ein Heptadecagon Seiten von 2 cm hat? Finden Sie auch den Wert des Umfangs.

Um die Frage zu beantworten, muss die Beziehung zwischen der Seite und dem Radius eines regulären n-seitigen Polygons berücksichtigt werden:

 d = 2 r Sen (180º / n)

Für das Siebeneck n = 17, so dass d = 0,3675 r, das heißt, der Radius des Heptadecagons beträgt r = 2 cm / 0,3675 = 5,4423 cm oder

10,8844 cm Durchmesser.

Der Umfang eines 2 cm seitlichen Heptadecagons beträgt P = 17 · 2 cm = 34 cm.

Beispiel 2

Was ist die Fläche eines regulären Siebenecks mit einer Seite von 2 cm?

Wir müssen uns auf die im vorherigen Abschnitt gezeigte Formel beziehen, die es uns ermöglicht, die Fläche eines Siebeneckens zu finden, wenn es die Länge hat d auf deiner Seite:

Heptadecagon-Bereich = (17/4) (d^zwei) / Tan (180º / 17) 

Beim Ersetzen d = 2 cm in der obigen Formel erhalten Sie:

Bereich = 90,94 cm

Verweise

1. C. E. A. (2003). Elemente der Geometrie: mit Übungen und Geometrie des Kompasses. Universität von Medellin.
2. Campos, F., Cerecedo, F. J. (2014). Mathematik 2. Grupo Editorial Patria.
3. Freed, K. (2007). Entdecken Sie Polygone. Benchmark Education Company.
4. Hendrik, V. (2013). Verallgemeinerte Polygone. Birkhäuser.
5. IGER. (s.f.). Mathematik Erstes Semester Tacaná. IGER.
6. Jr. Geometrie. (2014). Polygone. Lulu Press, Inc..
7. Miller, Heeren & Hornsby. (2006). Mathematik: Argumentation und Anwendungen (Zehnte Ausgabe). Pearson Ausbildung.
8. Patiño, M. (2006). Mathematik 5. Editorial Progreso.
9. Sada, M. 17-seitiges reguläres Polygon mit Lineal und Kompass. Wiederhergestellt von: geogebra.org
10. Wikipedia. Heptadecagon. Wiederhergestellt von: es.wikipedia.com