Freiheitsgrade, wie man sie berechnet, Typen, Beispiele

Das Freiheitsgrade In der Statistik sind sie die Anzahl unabhängiger Komponenten eines Zufallsvektors. Wenn der Vektor hat n Komponenten und es gibt p lineare Gleichungen, die ihre Komponenten in Beziehung setzen, dann die Freiheitsgrad ist n-p.

Das Konzept von Freiheitsgrade Es erscheint auch in der theoretischen Mechanik, wo sie ungefähr der Raumdimension entsprechen, in der sich das Teilchen bewegt, abzüglich der Anzahl der Bindungen..

In diesem Artikel wird das Konzept der Freiheitsgrade für Statistiken erörtert. Ein mechanisches Beispiel ist jedoch in geometrischer Form leichter zu visualisieren.

Artikelverzeichnis

• 1 Arten von Freiheitsgraden
  • 1.1 In einem mechanischen Fall
  • 1.2 In einer Reihe von Zufallswerten
• 2 Beispiele
  • 2.1 Varianz und Freiheitsgrade
  • 2.2 In der Chi-Quadrat-Verteilung
  • 2.3 Beim Testen von Hypothesen (mit ausgearbeitetem Beispiel)
• 3 Referenzen

Arten von Freiheitsgraden

Abhängig vom Kontext, in dem es angewendet wird, kann die Art und Weise der Berechnung der Anzahl der Freiheitsgrade variieren, aber die zugrunde liegende Idee ist immer dieselbe: Gesamtdimensionen minus Anzahl der Einschränkungen.

In einem mechanischen Fall

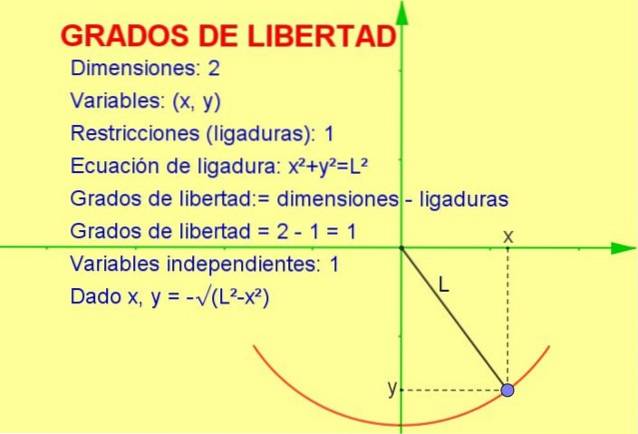
Betrachten wir ein oszillierendes Teilchen, das an eine Schnur (ein Pendel) gebunden ist, die sich in der vertikalen x-y-Ebene (2 Dimensionen) bewegt. Das Teilchen ist jedoch gezwungen, sich auf dem Umfang des Radius zu bewegen, der der Länge der Sehne entspricht.

Da sich das Teilchen nur auf dieser Kurve bewegen kann, ist die Anzahl der Freiheitsgrade ist 1. Dies ist in Abbildung 1 zu sehen.

Die Anzahl der Freiheitsgrade wird berechnet, indem die Differenz aus der Anzahl der Dimensionen abzüglich der Anzahl der Einschränkungen genommen wird:

Freiheitsgrade: = 2 (Dimensionen) - 1 (Ligatur) = 1

Eine weitere Erklärung, die es uns ermöglicht, zum Ergebnis zu gelangen, ist die folgende:

-Wir wissen, dass die Position in zwei Dimensionen durch einen Koordinatenpunkt (x, y) dargestellt wird..

-Da aber der Punkt die Gleichung des Umfangs erfüllen muss (x^zwei + Y.^zwei = L.^zwei) Für einen gegebenen Wert der Variablen x wird die Variable y durch die Gleichung oder Einschränkung bestimmt.

Somit ist nur eine der Variablen unabhängig und das System hat ein (1) Freiheitsgrad.

In einer Reihe von Zufallswerten

Um zu veranschaulichen, was das Konzept bedeutet, nehmen wir den Vektor an

x = (x₁, x_zwei,..., x_n)

Was repräsentiert die Stichprobe von n normalverteilte Zufallswerte. In diesem Fall der Zufallsvektor x haben n unabhängige Komponenten und daher wird gesagt, dass x haben n Freiheitsgrade.

Nun bauen wir den Vektor r von Verschwendung

r = (x₁ - , x_zwei - ,…., X._n - )

Wo stellt den Stichprobenmittelwert dar, der wie folgt berechnet wird:

= (x₁ + x_zwei +…. + X._n) / n

Also die Summe

(x₁ - ) + (x_zwei - ) +…. + (X._n - ) = (x₁ + x_zwei +…. + X._n) - n= 0

Es ist eine Gleichung, die eine Einschränkung (oder Bindung) für die Elemente des Vektors darstellt r der Reste, da wenn n-1 Komponenten des Vektors bekannt sind r, Die Beschränkungsgleichung bestimmt die unbekannte Komponente.

Daher der Vektor r der Dimension n mit der Einschränkung:

∑ (x_ich - ) = 0

Haben (n - 1) Freiheitsgrade.

Wiederum wird angewendet, dass die Berechnung der Anzahl der Freiheitsgrade ist:

Freiheitsgrade: = n (Dimensionen) - 1 (Einschränkungen) = n-1

Beispiele

Varianz und Freiheitsgrade

Die Varianz s^zwei ist definiert als der Mittelwert des Quadrats der Abweichungen (oder Residuen) der Stichprobe von n Daten:

s^zwei = (r• •r) / (n-1)

wo r ist der Vektor der Residuen r = (x1 - , x2 - ,…., Xn - ) und die dicke Spitze (• •) ist der skalare Produktoperator. Alternativ kann die Varianzformel wie folgt geschrieben werden:

s^zwei = ∑ (x_ich - )^zwei / (n-1)

In jedem Fall sollte beachtet werden, dass bei der Berechnung des Mittelwerts des Quadrats der Residuen dieser durch (n-1) und nicht durch n geteilt wird, da, wie im vorherigen Abschnitt erläutert, die Anzahl der Freiheitsgrade der Vektor r ist (n-1).

Wenn für die Berechnung der Varianz geteilt wurde durch n anstelle von (n-1) hätte das Ergebnis eine Verzerrung, die für Werte von sehr signifikant ist n unter 50.

In der Literatur erscheint die Varianzformel auch mit dem Divisor n anstelle von (n-1), wenn es um die Varianz einer Population geht.

Aber die Menge der Zufallsvariablen der Residuen, dargestellt durch den Vektor r, Obwohl es die Dimension n hat, hat es nur (n-1) Freiheitsgrade. Wenn jedoch die Anzahl der Daten groß genug ist (n> 500), konvergieren beide Formeln zum gleichen Ergebnis.

Taschenrechner und Tabellen liefern sowohl Versionen der Varianz als auch die Standardabweichung (die Quadratwurzel der Varianz)..

In Anbetracht der hier vorgestellten Analyse empfehlen wir, immer die Version mit (n-1) zu wählen, wenn die Varianz oder Standardabweichung berechnet werden muss, um verzerrte Ergebnisse zu vermeiden..

In der Chi-Quadrat-Verteilung

Einige Wahrscheinlichkeitsverteilungen in kontinuierlichen Zufallsvariablen hängen von einem aufgerufenen Parameter ab Freiheitsgrad, ist der Fall der Chi-Quadrat-Verteilung (χ^zwei).

Der Name dieses Parameters ergibt sich genau aus den Freiheitsgraden des zugrunde liegenden Zufallsvektors, für den diese Verteilung gilt.

Angenommen, wir haben g Populationen, aus denen Proben der Größe n entnommen werden:

X.₁ = (x1₁, x1_zwei,… X1_n)

X2 = (x2₁, x2_zwei,… X2_n)

... .

X._j = (xj₁, xj_zwei,… Xj_n)

... .

Xg = (xg₁, xg_zwei,… Xg_n)

Eine Bevölkerung j was hat durchschnittlich und Standardabweichung Sj, folgt der Normalverteilung N (, Sj ).

Die standardisierte oder normalisierte Variable zj_ich ist definiert als:

zj_ich = (xj_ich - ) / Sj.

Und der Vektor Zj ist wie folgt definiert:

Zj = (zj₁, zj_zwei,..., zj_ich,..., zj_n) und folgt der standardisierten Normalverteilung N (0,1).

Also die Variable:

Q. = ((z1₁ ^ 2 + z2₁^ 2 +…. + zg₁^ 2),…., (Z1_n^ 2 + z2_n^ 2 +…. + zg_n^ 2))

Folgen Sie der Verteilung χ^zwei(g) genannt die Chi-Quadrat-Verteilung mit Freiheitsgrad G.

Im Hypothesentest (Mit Beispiel ausgearbeitet)

Wenn Sie Hypothesen basierend auf einem bestimmten Satz zufälliger Daten testen möchten, müssen Sie die kennen Anzahl der Freiheitsgrade g um den Chi-Quadrat-Test anwenden zu können.

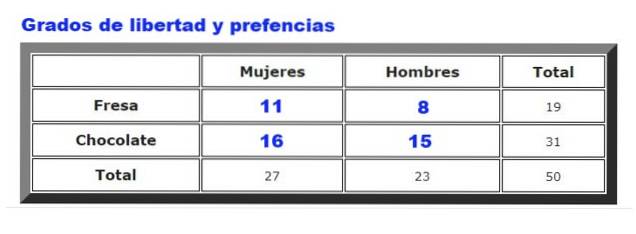
Als Beispiel werden die Daten analysiert, die zu den Vorlieben von Schokolade oder Erdbeereis bei Männern und Frauen in einer bestimmten Eisdiele erhoben wurden. Die Häufigkeit, mit der Männer und Frauen Erdbeere oder Schokolade wählen, ist in Abbildung 2 zusammengefasst.

Zunächst wird die Tabelle der erwarteten Frequenzen berechnet, die durch Multiplikation der erstellt wird Gesamtanzahl der Zeilen für ihn Gesamtspalten, geteilt durch Gesamtdaten. Das Ergebnis ist in der folgenden Abbildung dargestellt:

Dann berechnen wir das Chi-Quadrat (aus den Daten) mit der folgenden Formel:

χ^zwei = ∑ (F._oder - F._und)^zwei / F._und

Wo F._oder sind die beobachteten Frequenzen (Abbildung 2) und F._und sind die erwarteten Frequenzen (Abbildung 3). Die Summierung geht über alle Zeilen und Spalten, die in unserem Beispiel vier Begriffe ergeben.

Nach den Operationen erhalten Sie:

χ^zwei = 0,2043.

Nun ist es notwendig, mit dem theoretischen Chi-Quadrat zu vergleichen, das von der abhängt Anzahl der Freiheitsgrade g.

In unserem Fall wird diese Anzahl wie folgt bestimmt:

g = (# Zeilen - 1) (# Spalten - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Es stellt sich heraus, dass die Anzahl der Freiheitsgrade g in diesem Beispiel 1 ist.

Wenn Sie die Nullhypothese (H0: es besteht keine Korrelation zwischen GESCHMACK und GESCHLECHT) mit einem Signifikanzniveau von 1% überprüfen oder ablehnen möchten, wird der theoretische Chi-Quadrat-Wert mit dem Freiheitsgrad g = 1 berechnet.

Es wird der Wert gesucht, der die akkumulierte Frequenz (1 - 0,01) = 0,99, dh 99% macht. Dieser Wert (der aus den Tabellen entnommen werden kann) beträgt 6,636.

Wenn das theoretische Chi das berechnete überschreitet, wird die Nullhypothese verifiziert.

Das heißt, mit den gesammelten Daten, Nicht beobachtet Beziehung zwischen den Variablen TASTE und GENDER.

Verweise

1. Minitab. Was sind die Freiheitsgrade? Wiederhergestellt von: support.minitab.com.
2. Moore, David. (2009) Grundlegende angewandte Statistik. Antoni Bosch Herausgeber.
3. Leigh, Jennifer. Berechnung von Freiheitsgraden in statistischen Modellen. Wiederhergestellt von: geniolandia.com
4. Wikipedia. Freiheitsgrad (Statistik). Wiederhergestellt von: es.wikipedia.com
5. Wikipedia. Freiheitsgrad (physisch). Wiederhergestellt von: es.wikipedia.com