
Grad eines Polynoms, wie es bestimmt wird, Beispiele und Übungen
Das Grad eines Polynoms auf ein Variable ist gegeben durch den Term, der den größten Exponenten hat, und wenn das Polynom hat zwei oder mehr Variablen, dann wird der Grad durch die Summe der Exponenten jedes Terms bestimmt, wobei die größere Summe der Grad des Polynoms ist.
Mal sehen, wie man den Grad des Polynoms auf praktische Weise bestimmt.

Angenommen, das Polynom P (x) = -5x + 8x3 + 7 - 4xzwei. Dieses Polynom ist eine Variable, in diesem Fall die Variable x. Dieses Polynom besteht aus mehreren Begriffen:
-5x; 8x3;; 7; - 4xzwei
Wählen wir aus den vier Begriffen den aus, dessen Exponent größer ist. Dieser Begriff lautet:
8x3
Und was ist nun der Exponent? Die Antwort ist 3. Daher ist P (x) ein Polynom vom Grad 3.
Wenn das betreffende Polynom mehr als eine Variable hat, kann der Grad sein:
-Absolut
-In Bezug auf eine Variable
Der absolute Grad wird wie zu Beginn erläutert ermittelt: Addieren der Exponenten jedes Terms und Auswählen des größten.
Andererseits ist der Grad des Polynoms in Bezug auf eine der Variablen oder Buchstaben der größte Wert des Exponenten, den dieser Buchstabe hat. Der Punkt wird anhand der Beispiele und gelösten Übungen in den folgenden Abschnitten klarer.
Artikelverzeichnis
- 1 Beispiele für den Grad eines Polynoms
- 1.1 Tabelle 1. Beispiele für Polynome und ihre Grade
- 2 Verfahren zum Arbeiten mit Polynomen
- 2.1 Ordnen, reduzieren und vervollständigen Sie ein Polynom
- 2.2 Bedeutung des Grads eines Polynoms zusätzlich und subtrahiert
- 3 Gelöste Übungen
- 3.1 - Übung gelöst 1
- 3.2 - Übung gelöst 2
- 4 Referenzen
Beispiele für den Grad eines Polynoms
Polynome können nach Grad klassifiziert werden und können erster Grad, zweiter Grad, dritter Grad usw. sein. Für das Beispiel in Abbildung 1 ist die Energie ein Monom ersten Grades für die Masse.
Es ist auch wichtig zu beachten, dass die Anzahl der Terme, die ein Polynom hat, gleich ist Note plus 1. A) Ja:
-Polynome ersten Grades haben zwei Terme: a1x + aoder
-Das Polynom zweiten Grades hat drei Terme: azweixzwei + zu1x + aoder
-Ein Polynom dritten Grades hat 4 Terme: a3x3 + zuzweixzwei + zu1x + aoder
Und so weiter. Der aufmerksame Leser wird bemerkt haben, dass die Polynome in den vorherigen Beispielen in der Form geschrieben sind abnehmend, Das heißt, der Begriff steht an erster Stelle mit dem Höchste Note.
Die folgende Tabelle zeigt verschiedene Polynome, sowohl einer als auch mehrerer Variablen und ihrer jeweiligen absolute Grade::
Tabelle 1. Beispiele für Polynome und ihre Grade
| Polynom | Klasse |
|---|---|
| 3x4+5x3-2x + 3 | 4 |
| 7x3-2xzwei+3x-6 | 3 |
| 6 | 0 |
| x-1 | 1 |
| x5-bx4+abx3+ab3xzwei | 6 |
| 3x3Y.5 + 5xzweiY.4 - 7xyzwei + 6 | 8 |
Die letzten beiden Polynome haben mehr als eine Variable. Von diesen wurde der Begriff mit dem höchsten absoluten Grad fett hervorgehoben, damit der Leser den Grad schnell überprüfen kann. Es ist wichtig zu bedenken, dass, wenn die Variable keinen geschriebenen Exponenten hat, dieser Exponent gleich 1 ist.
Zum Beispiel im vorgestellten Begriff ab3xzwei Es gibt drei Variablen, nämlich: zu, b Y. x. In diesem Begriff, zu wird auf 1 erhöht, das heißt:
a = a1
Deshalb ab3xzwei = a1b3xzwei
Da der Exponent von b 3 und der von x 2 ist, folgt unmittelbar, dass der Grad dieses Terms ist:
1 + 3 + 2 = 6
Y ist der absolute Grad des Polynoms, da kein anderer Term einen höheren Grad hat.
Verfahren zum Arbeiten mit Polynomen
Bei der Arbeit mit Polynomen ist es wichtig, auf den Grad zu achten, da es zweckmäßig ist, zuerst und vor jeder Operation die folgenden Schritte auszuführen, bei denen der Grad sehr wichtige Informationen liefert:
-Ordnen Sie das bevorzugte Polynom in abnehmender Richtung. Auf diese Weise befindet sich der Begriff mit dem höchsten Grad links und der Begriff mit dem niedrigsten Grad rechts..
-Reduzieren Sie gleiche Begriffe, eine Prozedur, bei der alle Begriffe derselben Variablen und des gleichen Grades, die im Ausdruck enthalten sind, algebraisch addiert werden.
-Falls erforderlich, werden die Polynome vervollständigt und Terme mit einem Koeffizienten von 0 eingefügt, falls Terme mit einem Exponenten fehlen.
Ordnen, reduzieren und vervollständigen Sie ein Polynom
Gegeben ist das Polynom P (x) = 6xzwei - 5x4- 2x + 3x + 7 + 2x5 - 3x3 + x7 -12 Es wird gebeten, es in absteigender Reihenfolge zu bestellen, die ähnlichen Begriffe zu reduzieren, falls vorhanden, und die fehlenden Begriffe gegebenenfalls zu vervollständigen.
Das erste, wonach gesucht werden muss, ist der Begriff mit dem größten Exponenten, dem Grad des Polynoms, der sich als folgender herausstellt:
x7
Daher hat P (x) den Grad 7. Als nächstes wird das Polynom geordnet, beginnend mit diesem Term auf der linken Seite:
P (x) = x7 + 2x5 - 5x4 - 3x3 + 6xzwei - 2x + 3x + 7 -12
Nun werden die gleichen Begriffe reduziert, die folgende sind: - 2x und 3x einerseits. Und 7 und -12 auf der anderen Seite. Um sie zu reduzieren, werden die Koeffizienten algebraisch addiert und die Variable bleibt unverändert (wenn die Variable nicht neben dem Koeffizienten angezeigt wird, denken Sie daran, dass x0 = 1):
-2x + 3x = x
7-12 = -5
Ersetzen Sie diese Ergebnisse in P (x):
P (x) = x7 +2x5 - 5x4 - 3x3 + 6xzwei + x -5
Und schließlich wird das Polynom untersucht, um festzustellen, ob ein Exponent fehlt, und tatsächlich fehlt ein Term, dessen Exponent 6 ist. Daher wird es mit folgenden Nullen vervollständigt:
P (x) = x7 + 0x6 +2x5 - 5x4 - 3x3 + 6xzwei + x - 5
Nun wird beobachtet, dass das Polynom mit 8 Termen belassen wurde, da, wie zuvor gesagt, die Anzahl der Terme gleich Grad + 1 ist.
Bedeutung des Grades eines Polynoms zusätzlich und subtrahiert
Mit Polynomen können Sie Additions- und Subtraktionsoperationen ausführen, bei denen nur gleiche Terme addiert oder subtrahiert werden, dh solche mit derselben Variablen und demselben Grad. Wenn es keine ähnlichen Begriffe gibt, wird die Addition oder Subtraktion einfach angezeigt.
Sobald die Addition oder Subtraktion durchgeführt wurde, wobei letztere die Summe des Gegenteils ist, ist der Grad des resultierenden Polynoms immer gleich oder kleiner als der Grad des Polynoms, das den höchsten Grad addiert.
Gelöste Übungen
- Gelöste Übung 1
Finden Sie die folgende Summe und bestimmen Sie ihren absoluten Grad:
zu3- 8axzwei + x3 + 5 ..zweix - 6axzwei - x3 + 3 ..3 - 5 ..zweix - x3 + zu3+ 14axzwei - x3
Lösung
Es ist ein Polynom mit zwei Variablen, daher ist es zweckmäßig, ähnliche Begriffe zu reduzieren:
zu3- 8axzwei + x3 + 5 ..zweix - 6axzwei - x3 + 3 ..3 - 5 ..zweix - x3 + zu3+ 14axzwei - x3 =
= a3 + 3 ..3 + zu3 - 8axzwei - 6axzwei+ 14axzwei +5 ..zweix - 5 ..zweix + x3- x3- x3- x3 =
= 5a3 - 2x3
Beide Begriffe haben in jeder Variablen den Grad 3. Daher beträgt der absolute Grad des Polynoms 3.
- Übung gelöst 2
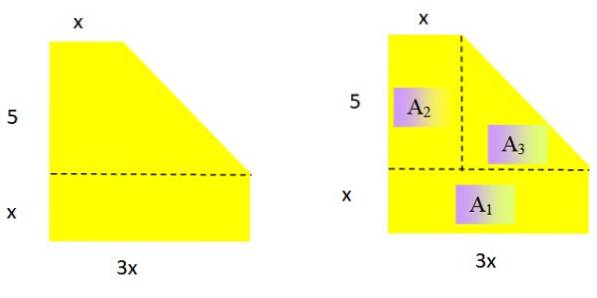
Drücken Sie den Bereich der folgenden ebenen geometrischen Figur als Polynom aus (Abbildung 2 links). Was ist der Grad des resultierenden Polynoms??
Lösung
Als Fläche muss das resultierende Polynom in der Variablen x den Grad 2 haben. Um einen geeigneten Ausdruck für das Gebiet zu bestimmen, wird die Figur in bekannte Gebiete zerlegt:
Die Fläche eines Rechtecks und eines Dreiecks ist jeweils: Basis x Höhe Y. Basis x Höhe / 2
ZU1 = x. 3x = 3xzwei;; ZUzwei = 5. x = 5x; ZU3 = 5. (2x / 2) = 5x
Hinweis: Die Basis des Dreiecks ist 3x - x = 2x und seine Höhe ist 5.
Nun werden die drei erhaltenen Ausdrücke hinzugefügt, damit haben wir die Fläche der Figur als Funktion von x::
3xzwei + 5x + 5x = 3xzwei + 10x
Verweise
- Baldor, A. 1974. Elementare Algebra. Kultur Venezolana S.A..
- Jiménez, R. 2008. Algebra. Prentice Halle.
- Wikibooks. Polynome. Wiederhergestellt von: es. wikibooks.org.
- Wikipedia. Grad (Polynom). Wiederhergestellt von: es.wikipedia.org.
- Zill, D. 1984. Algebra und Trigonometrie. Mac Graw Hill.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.