
Homografische Funktion, wie grafisch dargestellte, gelöste Übungen
Das es funktioniertehomographisches oder rationales Ion Es ist eine Art mathematische Funktion, die sich aus der Division zweier Polynomkomponenten zusammensetzt. Es folgt der Form P (x) / Q (x), wobei Q (x) keine Nullform annehmen kann.
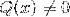
Zum Beispiel entspricht der Ausdruck (2x - 1) / (x + 3) einer homographischen Funktion mit P (x) = 2x - 1 und Q (x) = x + 3.

Die homografischen Funktionen bilden einen Teil der Untersuchung der analytischen Funktionen, der anhand des grafischen Ansatzes und der Untersuchung der Domäne und des Bereichs behandelt wird. Dies ist auf die Einschränkungen und Gründe zurückzuführen, die für ihre Beschlüsse gelten müssen..
Artikelverzeichnis
- 1 Was ist eine homografische Funktion??
- 2 Gemischte homografische Funktion
- 2.1 Gerade n-te Wurzel der homografischen Funktion
- 2.2 Logarithmus der homographischen Funktion
- 3 So zeichnen Sie eine homografische Funktion grafisch auf?
- 3.1 Wurzeln
- 3.2 Vertikale Asymptote
- 3.3 Horizontale Asymptote
- 3.4 Wachstumsintervall
- 3.5 Abklingintervall
- 3.6 Schnittpunkt mit Y.
- 4 Beispiele
- 4.1 Übung 1
- 4.2 Übung 1.2
- 5 Übung 2
- 6 Referenzen
Was ist eine homografische Funktion??
Sie sind rationale Ausdrücke einer einzelnen Variablen, obwohl dies nicht bedeutet, dass es keinen ähnlichen Ausdruck für zwei oder mehr Variablen gibt, bei denen es sich bereits um Körper im Raum handelt, die denselben Mustern wie die homografische Funktion in folgen das Flugzeug.
In einigen Fällen haben sie echte Wurzeln, aber das Vorhandensein vertikaler und horizontaler Asymptoten sowie Wachstums- und Abnahmeintervalle bleibt immer erhalten. Im Allgemeinen ist nur einer dieser Trends vorhanden, aber es gibt Ausdrücke, die beides in ihrer Entwicklung zeigen können..
Seine Domäne wird durch die Wurzeln des Nenners begrenzt, da die reellen Zahlen nicht durch Null geteilt werden.
Gemischte homografische Funktion
Sie sind sehr häufig in der Berechnung, insbesondere Differential und Integral, und sind notwendig, um unter bestimmten Formeln abzuleiten und zu antiderivieren. Einige der häufigsten sind unten aufgeführt.
Sogar die n-te Wurzel der homografischen Funktion
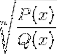
Schließen Sie alle Elemente aus der Domäne aus, die das Argument negativ machen. Die in jedem Polynom vorhandenen Wurzeln ergeben bei Auswertung Werte von Null.
Diese Werte werden vom Radikal akzeptiert, obwohl die grundlegende Einschränkung der homografischen Funktion berücksichtigt werden muss. Wobei Q (x) keine Nullwerte empfangen kann.
Die Lösungen der Intervalle müssen abgefangen werden:
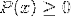
Um die Lösung der Schnittpunkte zu erreichen, kann unter anderem die Zeichenmethode verwendet werden.
Logarithmus der homographischen Funktion
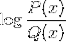
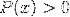
Es ist auch üblich, beide Ausdrücke unter anderem in einer Kombination zu finden.
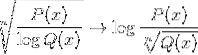
So zeichnen Sie eine homografische Funktion grafisch auf?
Homografische Funktionen entsprechen grafisch Hyperbeln in der Ebene. Welche horizontal und vertikal gemäß den Werten transportiert werden, die die Polynome definieren.
Es gibt mehrere Elemente, die wir definieren müssen, um eine rationale oder homografische Funktion grafisch darzustellen.
Nachlass
Das erste sind die Wurzeln oder Nullen der Funktionen P und Q..
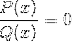
Die erreichten Werte werden auf der x-Achse des Diagramms angegeben. Anzeigen der Schnittpunkte des Diagramms mit der Achse.
Vertikale Asymptote
Sie entsprechen vertikalen Linien, die den Graphen anhand der Trends abgrenzen, die diese darstellen. Sie berühren die x-Achse bei den Werten, die den Nenner auf Null setzen, und werden vom Diagramm der homografischen Funktion niemals berührt.
Horizontale Asymptote
Dargestellt durch eine horizontale Stichlinie, grenzt sie eine Grenze ab, für die die Funktion nicht genau am Punkt definiert wird. Trends werden vor und nach dieser Linie beobachtet.
Um es zu berechnen, müssen wir auf eine Methode zurückgreifen, die der Methode von L'Hopital ähnelt und verwendet wird, um Grenzen rationaler Funktionen zu lösen, die zur Unendlichkeit neigen. Wir müssen die Koeffizienten der höchsten Potenzen im Zähler und Nenner der Funktion nehmen.
Zum Beispiel hat der folgende Ausdruck eine horizontale Asymptote bei y = 2/1 = 2.
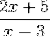
Wachstumsintervall
Bei den Ordinatenwerten sind aufgrund der Asymptoten Trends in der Grafik markiert. Im Falle eines Wachstums nimmt die Funktion an Wert zu, wenn die Elemente der Domäne von links nach rechts ausgewertet werden.
Intervall verringern
Die Ordinatenwerte nehmen ab, wenn die Domänenelemente von links nach rechts ausgewertet werden.
Die in den Werten gefundenen Sprünge werden nicht berücksichtigt, wenn sie zunehmen oder abnehmen. Dies tritt auf, wenn sich der Graph in der Nähe einer vertikalen oder horizontalen Asymptote befindet, wobei die Werte von unendlich bis negativ unendlich und umgekehrt variieren können..
Y-Kreuzung
Indem wir den Wert von x auf Null setzen, finden wir den Achsenabschnitt mit der Ordinatenachse. Dies ist eine sehr nützliche Information, um den Graphen der rationalen Funktion zu erhalten.
Beispiele
Definieren Sie das Diagramm der folgenden Ausdrücke, finden Sie deren Wurzeln, vertikale und horizontale Asymptoten, Wachstums- und Abnahmeintervalle und Schnittpunkte mit der Ordinatenachse.
Übung 1
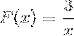
Der Ausdruck hat keine Wurzeln, da er im Zähler einen konstanten Wert hat. Die anzuwendende Einschränkung ist x verschieden von Null. Mit horizontaler Asymptote bei y = 0 und vertikaler Asymptote bei x = 0. Es gibt keine Schnittpunkte mit der y-Achse.
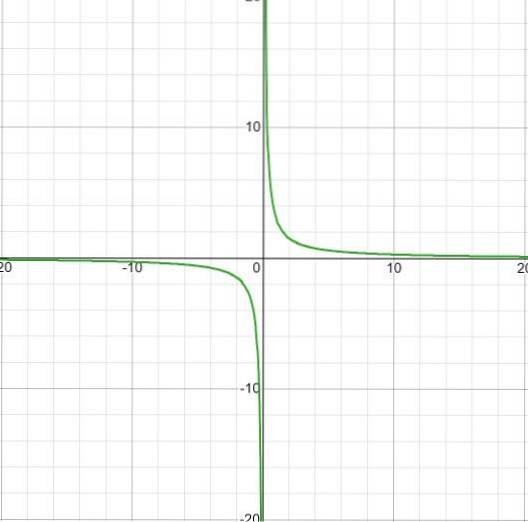
Es wird beobachtet, dass es auch beim Sprung von minus nach plus unendlich bei x = 0 keine Wachstumsintervalle gibt.
Das Abklingintervall beträgt
ID: (-∞; o) U (0, ∞)
Übung 1.2
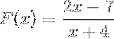
2 Polynome werden wie in der ursprünglichen Definition beobachtet, daher gehen wir gemäß den festgelegten Schritten vor.
Die gefundene Wurzel ist x = 7/2, was sich aus der Einstellung der Funktion auf Null ergibt.
Die vertikale Asymptote liegt bei x = - 4, was der Wert ist, der durch die Bedingung der rationalen Funktion aus der Domäne ausgeschlossen wird.
Die horizontale Asymptote liegt bei y = 2, dies nach Division von 2/1, den Koeffizienten der Variablen vom Grad 1.
Es hat einen y-Achsenabschnitt = - 7/4. Wert gefunden, nachdem x mit Null gleichgesetzt wurde.
Die Funktion wächst ständig mit einem Sprung von plus nach minus unendlich um die Wurzel x = -4.
Sein Wachstumsintervall beträgt (-∞, - 4) U (- 4, ∞).
Wenn sich der Wert von x minus unendlich nähert, nimmt die Funktion Werte nahe 2 an. Dasselbe passiert, wenn x sich mehr unendlich nähert.
Der Ausdruck nähert sich plus unendlich, wenn von links nach - 4 bewertet wird, und minus unendlich, wenn von rechts nach - 4 bewertet wird.
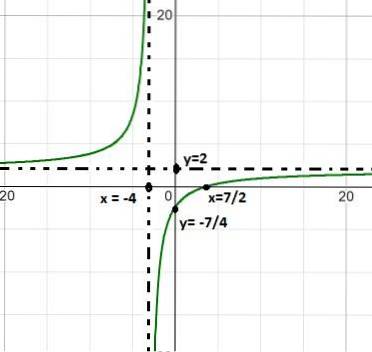
Übung 2
Der Graph der folgenden homographischen Funktion wird beobachtet:
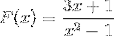
Beschreiben Sie das Verhalten, die Wurzeln, die vertikalen und horizontalen Asymptoten, die Wachstums- und Abnahmeintervalle sowie den Schnittpunkt mit der Ordinatenachse..
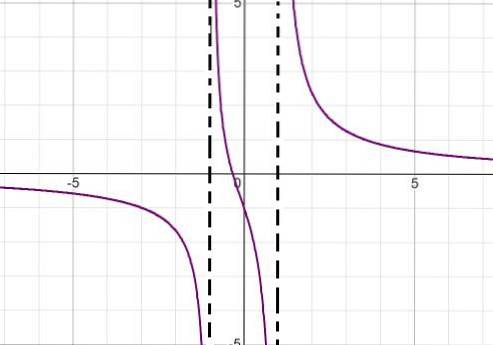
Der Nenner des Ausdrucks sagt uns, indem er die Differenz der Quadrate (x + 1) (x - 1) der Werte der Wurzeln berücksichtigt. Auf diese Weise können beide vertikalen Asymptoten definiert werden als:
x = -1 und x = 1
Die horizontale Asymptote entspricht der Abszissenachse, da die höchste Leistung im Nenner liegt.
Seine einzige Wurzel ist definiert durch x = -1/3.
Der Ausdruck nimmt immer von links nach rechts ab. Es nähert sich Null, wenn es sich der Unendlichkeit nähert. Minus unendlich, wenn Sie sich -1 von links nähern. Ein Plus unendlich, wenn es sich von rechts -1 nähert. Minus unendlich, wenn Sie sich 1 von links nähern, und mehr unendlich, wenn Sie sich 1 von rechts nähern.
Verweise
- Approximation mit rationalen Funktionen. Donald J. Newman. American Mathematical Soc., 31. Dezember. 1979
- Orthogonale rationale Funktionen. UNIVERSIDAD DE LA LAGUNA TENERIFE ADHEMAR BULTHEEL, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen und Olav Njastad. Cambridge University Press, 13. Februar. 1999
- Rationale Approximation realer Funktionen. P.P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. März. 2011
- Algebraische Funktionen. Gilbert Ames Bliss. Courier Corporation, 1. Januar 2004
- Zeitschrift der Spanischen Mathematischen Gesellschaft, Bände 5-6. Spanische Mathematische Gesellschaft, Madrid 1916



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.