
Statischer Reibungskoeffizient, Beispiel Übung

Das statische Reibung ist die Kraft, die zwischen zwei Oberflächen entsteht, wenn eine Oberfläche nicht in Bezug auf die andere gleitet. Es ist von großer Bedeutung, da es uns ermöglicht, uns beim Gehen vorwärts zu bewegen, da es die Kraft ist, die zwischen dem Boden und der Sohle der Schuhe vorhanden ist.
Es ist auch statische Reibung, die zwischen dem Bürgersteig und den Reifen des Autos auftritt. Wenn diese Kraft nicht vorhanden ist, kann sich das Auto nicht in Bewegung setzen, wie dies bei einem Auto der Fall ist, das versucht, auf einer eisigen Oberfläche zu starten: Die Räder rutschen, aber das Auto bewegt sich nicht.

Die Haftreibung hängt von der Rauheit der berührenden Oberflächen und auch von der Art des Materials ab, aus dem sie bestehen. Deshalb bestehen die Reifen und Sportschuhe aus Gummi, um die Reibung auf dem Bürgersteig zu erhöhen..
Im Haftreibungsmodell werden die Materialeigenschaften und der Rauheitsgrad zwischen den Oberflächen in einer so genannten Zahl zusammengefasst Haftreibungskoeffizient, welches experimentell bestimmt wird.
Artikelverzeichnis
- 1 Haftreibungskoeffizient
- 2 Beispiel: Bestimmung des Haftreibungskoeffizienten
- 3 Übung
- 3.1 Lösung
- 4 Referenzen
Statischer Reibungskoeffizient

Die obige Abbildung zeigt ein Buch, das auf einem Tisch mit einer Neigung von 15,7 ° ruht.
Wenn die Oberflächen des Buches und des Tisches sehr glatt und poliert wären, könnte das Buch nicht stillstehen. Da dies jedoch nicht der Fall ist, erscheint eine Kraft, die die Kontaktflächen tangiert und als Kraft von bezeichnet wird statische Reibung.
Wenn der Neigungswinkel groß genug ist, ist nicht genug vorhanden statische Reibungskraft um das Buch zu balancieren und es würde anfangen zu rutschen.
In diesem Fall gibt es auch Reibung zwischen dem Buch und dem Tisch, aber das wäre eine Stärke von dynamische Reibung, auch genannt kinetische Reibung.
Es gibt eine Grenze zwischen Haftreibung und dynamischer Reibung, die auftritt, wenn die Haftreibung ihren Maximalwert erreicht.
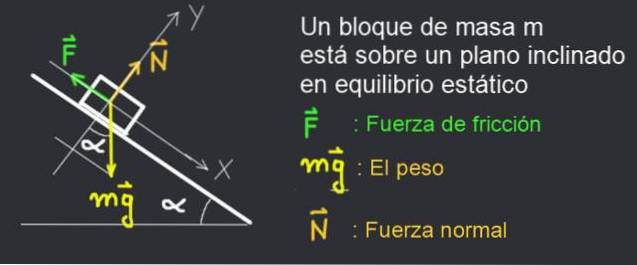
Betrachten wir in Abbildung 2 das Kraftdiagramm eines Massenbuchs m, das auf einer Neigungsebene α in Ruhe gehalten wird.
Das Buch bleibt in Ruhe, da die Haftreibungskraft F das System ausgleicht.
Wenn der Neigungswinkel ein wenig zunimmt, müssen die Kontaktflächen mehr Reibungskraft liefern, aber der Betrag der Haftreibung, den die Kontaktflächen bereitstellen können, hat eine maximale Grenze F.max, nämlich:
F ≤ F.max.
Die maximale Haftreibungskraft hängt von den Materialien und dem Grad der Rauheit der berührenden Oberflächen sowie der Festigkeit des Griffs ab.
Der Haftreibungskoeffizient μund ist eine positive Zahl, die von den Eigenschaften der Kontaktflächen abhängt. Normale Kraft N. dass die Ebene auf den Block wirkt, zeigt den Grad der Dichtheit zwischen der Oberfläche des Blocks und der Ebene. Auf diese Weise bestimmen sie die maximale Reibungskraft, die Oberflächen bereitstellen, wenn kein Gleiten erfolgt:
F.max = μund N.
Zusammenfassend folgt die Haftreibungskraft dem folgenden Modell:
F ≤ μund N.
Beispiel: Bestimmung des Haftreibungskoeffizienten
Der Haftreibungskoeffizient ist eine dimensionslose Zahl, die experimentell für jedes Oberflächenpaar bestimmt wird.
Wir betrachten den Block in Abbildung 2 in Ruhe. Die folgenden Kräfte wirken auf ihn:
- Reibungskraft: F.
- Das Gewicht des Massenblocks m: mG
- Normale Kraft: N.
Da der Block in Ruhe ist und keine Beschleunigung aufweist, ist nach dem zweiten Newtonschen Gesetz die resultierende Kraft - eine Vektorsumme - Null:
F. + N. + mG = 0
Ein festes XY-Koordinatensystem wird mit der X-Achse entlang der schiefen Ebene und der Y-Achse senkrecht dazu betrachtet, wie in Abbildung 2 dargestellt.
Die Kräfte müssen nach ihren kartesischen Komponenten getrennt werden, wodurch das folgende Gleichungssystem entsteht:
-Komponente X.: -F + mg Sen (α) = 0
-Komponente Y.: N - mg Cos (α) = 0
Der Wert der Haftreibungskraft ergibt sich aus der ersten Gleichung:
F = mg Sen (α)
Und ab der Sekunde der Wert der Normalkraft:
N = mg Cos (α)
Die Haftreibungskraft F folgt dem folgenden Modell:
F ≤ μund N.
Einsetzen der zuvor erhaltenen Werte in die Ungleichung, die wir haben:
mg Sen (α) ≤ μund mg Cos (α)
Unter Berücksichtigung der Tatsache, dass für Werte von α zwischen 0º und 90º sowohl die Sinus- als auch die Cosinusfunktion positiv sind und dass der Quotient zwischen Sinus und Cosinus die Tangente ist, haben wir:
Tan (α) ≤ μund
Die Gleichheit gilt für einen bestimmten Wert von α, der als kritischer Winkel bezeichnet wird und den wir mit α * bezeichnen, dh:
μund = Tan (α *)
Der kritische Winkel wird experimentell bestimmt, wobei die Neigung allmählich erhöht wird, bis der rechte Winkel erreicht ist, unter dem der Block zu gleiten beginnt, dh der kritische Winkel α *.
In dem Buch von 1 wurde dieser Winkel experimentell bestimmt, was zu 24 ° führte. Dann ist der Haftreibungskoeffizient:
μund = Tan (24º) = 0,45.
Es ist eine positive Zahl zwischen 0 und unendlich. Wenn μund = 0 Die Oberflächen sind perfekt glatt. Wenn μund → ∞ Die Oberflächen sind perfekt verbunden oder geschweißt.
Im Allgemeinen liegt der Wert des Reibungskoeffizienten zwischen 0 und 10.
Übung
Bei Sprint- oder Dragsterrennen werden beim Start Beschleunigungen von bis zu 4 g erreicht, die genau dann erreicht werden, wenn die Reifen nicht in Bezug auf die Fahrbahn rutschen..
Dies liegt daran, dass der Haftreibungskoeffizient immer größer als der dynamische Reibungskoeffizient ist..
Unter der Annahme, dass das Gesamtgewicht des Fahrzeugs plus Fahrer 600 kg beträgt und die Hinterräder 80% des Gewichts tragen, bestimmen Sie die Haftreibungskraft während des 4-g-Starts und den Haftreibungskoeffizienten zwischen Reifen und Fahrbahn..

Lösung
Nach dem zweiten Newtonschen Gesetz ist die resultierende Kraft gleich der Gesamtmasse des Fahrzeugs multipliziert mit der Beschleunigung, die es erhält.
Wenn sich das Fahrzeug im vertikalen Gleichgewicht befindet, heben sich die Normalen und das Gewicht auf, wodurch als Ergebnis die Reibungskraft F verbleibt, die die Fahrbahn auf die Kontaktfläche der Traktionsräder ausübt, so dass:
F = m (4 g) = 600 kg (4 · 9,8 m / s)zwei) = 23520 N = 2400 kg-f
Dies bedeutet, dass die Zugkraft 2,4 Tonnen beträgt.
Die Reibungskraft, die das Rad auf den Boden ausübt, geht rückwärts, aber seine Reaktion, die gleich und entgegengesetzt ist, wirkt auf den Reifen und geht vorwärts. Das ist die Kraft, die das Fahrzeug antreibt.
Natürlich wird all diese Kraft von dem Motor erzeugt, der versucht, den Boden durch das Rad zurückzudrücken, aber das Rad und der Boden sind durch Reibungskraft gekoppelt.
Um den Haftreibungskoeffizienten zu bestimmen, verwenden wir die Tatsache, dass das erhaltene F die maximal mögliche Reibung ist, da wir uns an der Grenze der maximalen Beschleunigung befinden, daher:
F = μund N = μe (0,8 mg)
Die Tatsache, dass die hinteren Antriebsräder das 0,8-fache des Gewichts tragen, wurde berücksichtigt. Wenn wir nach dem Reibungskoeffizienten suchen, erhalten wir:
μund = F / (0,8 mg) = 23520 N / (0,8 × 600 kg × 9,8 m / s 2) = 5.
Schlussfolgerung: μund = 5.
Verweise
- Alonso M., Finn E. 1970. Physik Band I: Mechanik. Interamerikanischer Bildungsfonds S.A..
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Hewitt, P. 2012. Konzeptionelle Physik. Fünfte Ausgabe.
- Rex, A. 2011. Grundlagen der Physik. Pearson. 190-200.
- Jung, Hugh. 2015. Universitätsphysik mit moderner Physik. 14. Aufl. Pearson.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.