
Volumetrischer Durchfluss
Was ist Volumenstrom??
Das Volumetrischer Durchfluss Es ermöglicht die Bestimmung des Flüssigkeitsvolumens, das durch einen Abschnitt der Leitung fließt, und liefert ein Maß für die Geschwindigkeit, mit der sich das Fluid durch die Leitung bewegt. Daher ist seine Messung besonders in so unterschiedlichen Bereichen wie Industrie, Medizin, Bauwesen und Forschung interessant..
Das Messen der Geschwindigkeit eines Fluids (sei es eine Flüssigkeit, ein Gas oder ein Gemisch aus beiden) ist jedoch nicht so einfach wie das Messen der Geschwindigkeit der Verdrängung eines festen Körpers. Um die Geschwindigkeit eines Fluids zu kennen, ist es daher erforderlich, seinen Fluss zu kennen.
Diese und viele andere Fragen im Zusammenhang mit Flüssigkeiten werden von der als Strömungsmechanik bekannten Physik behandelt. Der Durchfluss ist definiert als die Menge an Flüssigkeit, die unter Berücksichtigung einer zeitlichen Einheit durch einen Abschnitt einer Leitung fließt, sei es eine Rohrleitung, eine Ölleitung, ein Fluss, ein Kanal, eine Blutleitung usw..
Das Volumen, das in einer Zeiteinheit durch einen bestimmten Bereich fließt, wird normalerweise berechnet, auch als Volumenstrom bezeichnet. Die Masse oder der Massenstrom, der zu einem bestimmten Zeitpunkt durch einen bestimmten Bereich fließt, wird ebenfalls definiert, obwohl er weniger häufig als der Volumenstrom verwendet wird..
Wie wird der Volumenstrom berechnet??
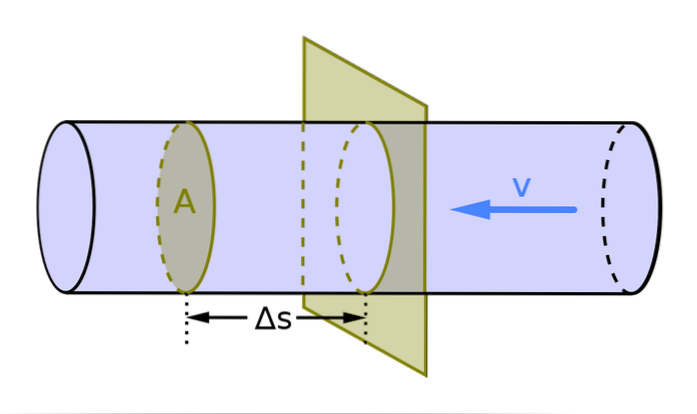
Der Volumenstrom wird durch den Buchstaben Q dargestellt. Für die Fälle, in denen sich der Durchfluss senkrecht zum Leiterabschnitt bewegt, wird er mit der folgenden Formel bestimmt:
Q = A = V / t
In dieser Formel ist A der Abschnitt des Leiters (es ist die durchschnittliche Geschwindigkeit des Fluids), V ist das Volumen und t ist die Zeit. Da im internationalen System die Fläche oder der Abschnitt des Leiters in m gemessen wirdzwei und die Geschwindigkeit in m / s wird der Durchfluss m gemessen3/ s.
Für die Fälle, in denen die Geschwindigkeit der Fluidverdrängung einen Winkel & thgr; mit der Richtung senkrecht zum Oberflächenabschnitt A erzeugt, ist der Ausdruck zum Bestimmen der Strömungsrate der folgende:
Q = A cos θ
Dies stimmt mit der vorherigen Gleichung überein, da, wenn die Strömung senkrecht zur Fläche A ist, & thgr; = 0 und daher cos & thgr; = 1 ist.
Die obigen Gleichungen gelten nur, wenn die Geschwindigkeit des Fluids gleichmäßig ist und wenn die Fläche des Abschnitts flach ist. Andernfalls wird der Volumenstrom durch das folgende Integral berechnet:
Q = ∫∫s v d S.
In diesem Integral ist dS der Oberflächenvektor, der durch den folgenden Ausdruck bestimmt wird:
dS = n dS
Dort ist n der Einheitsvektor senkrecht zur Kanaloberfläche und dS ein Oberflächendifferentialelement.
Kontinuitätsgleichung
Ein Merkmal inkompressibler Flüssigkeiten ist, dass die Masse der Flüssigkeit durch zwei Abschnitte erhalten bleibt. Aus diesem Grund ist die Kontinuitätsgleichung erfüllt, die die folgende Beziehung herstellt:
ρ1 ZU1 V.1 = ρzwei ZUzwei V.zwei
In dieser Gleichung ist ρ die Dichte des Fluids.
Für die Fälle von Regimen im permanenten Fluss, in denen die Dichte konstant ist und daher ρ wahr ist1 = ρzwei, läuft auf den folgenden Ausdruck hinaus:
ZU1 V.1 = A.zwei V.zwei
Dies ist gleichbedeutend mit der Bestätigung, dass der Fluss erhalten bleibt, und daher:
Q.1 = Q.zwei.
Aus der obigen Beobachtung folgt, dass Flüssigkeiten beschleunigen, wenn sie einen engeren Abschnitt einer Leitung erreichen, während sie langsamer werden, wenn sie einen breiteren Abschnitt einer Leitung erreichen. Diese Tatsache hat interessante praktische Anwendungen, da sie das Spielen mit der Bewegungsgeschwindigkeit einer Flüssigkeit ermöglicht.
Bernoullis Prinzip
Das Bernoulli-Prinzip bestimmt, dass für ein ideales Fluid (dh ein Fluid, das weder Viskosität noch Reibung aufweist), das sich im Kreislauf durch eine geschlossene Leitung bewegt, seine Energie während seiner gesamten Verdrängung konstant bleibt..
Letztendlich ist Bernoullis Prinzip nichts anderes als die Formulierung des Energieerhaltungsgesetzes für den Fluss einer Flüssigkeit. Somit kann die Bernoulli-Gleichung wie folgt formuliert werden:
h + vzwei / 2g + P / ρg = konstant
In dieser Gleichung ist h die Höhe und g ist die Erdbeschleunigung.
Die Bernoulli-Gleichung berücksichtigt zu jedem Zeitpunkt die Energie eines Fluids, eine Energie, die aus drei Komponenten besteht.
- Eine kinetische Komponente, die aufgrund der Geschwindigkeit, mit der sich die Flüssigkeit bewegt, Energie enthält.
- Eine Komponente, die durch das Gravitationspotential als Folge der Höhe der Flüssigkeit erzeugt wird.
- Eine Komponente der Strömungsenergie, dh die Energie, die ein Fluid aufgrund von Druck besitzt.
In diesem Fall wird die Bernoulli-Gleichung wie folgt ausgedrückt:
h ρ g + (vzwei ρ) / 2 + P = konstant
Logischerweise ist im Fall eines realen Fluids der Ausdruck der Bernoulli-Gleichung nicht erfüllt, da Reibungsverluste bei der Fluidverdrängung auftreten und es notwendig ist, auf eine komplexere Gleichung zurückzugreifen.
Was beeinflusst den Volumenstrom??
Der Volumenstrom wird beeinträchtigt, wenn der Kanal verstopft ist.
Darüber hinaus kann sich der Volumenstrom auch aufgrund von Temperatur- und Druckschwankungen in der realen Flüssigkeit ändern, die sich durch eine Leitung bewegt, insbesondere wenn es sich um ein Gas handelt, da das Volumen, das ein Gas einnimmt, in Abhängigkeit von Temperatur und Druck variiert beim.
Einfache Methode zur Messung des Volumenstroms
Eine wirklich einfache Methode zur Messung des Volumenstroms besteht darin, eine Flüssigkeit für einen bestimmten Zeitraum in einen Dosiertank fließen zu lassen..
Diese Methode ist im Allgemeinen nicht sehr praktisch, aber die Wahrheit ist, dass es äußerst einfach und sehr anschaulich ist, die Bedeutung und Wichtigkeit der Kenntnis der Durchflussrate einer Flüssigkeit zu verstehen..
Auf diese Weise kann das Fluid für einen bestimmten Zeitraum in einen Messbehälter fließen, das akkumulierte Volumen wird gemessen und das erhaltene Ergebnis durch die verstrichene Zeit geteilt.
Verweise
- Durchfluss (Flüssigkeit) (n.d.). Auf Wikipedia. Von es.wikipedia.org wiederhergestellt.
- Volumenstrom (n.d.). Auf Wikipedia. Von en.wikipedia.org wiederhergestellt.
- Ingenieure Edge, LLC. "Fluid Volumetric Flow Rate Equation". Engineers Edge
- Mott, Robert (1996). "1". Angewandte Strömungsmechanik (4. Auflage). Mexiko: Pearson Education.
- Batchelor, G.K. (1967). Eine Einführung in die Fluiddynamik. Cambridge University Press.
- Landau, L. D.; Lifshitz, E.M. (1987). Strömungsmechanik. Kurs für Theoretische Physik (2. Aufl.). Pergamonpresse.




Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.