
Beschreibende Statistikgeschichte, Merkmale, Beispiele, Konzepte
Das Beschreibende Statistik ist der Zweig der Statistik, der für das Sammeln und Organisieren von Informationen über das Verhalten von Systemen mit vielen Elementen verantwortlich ist, die allgemein unter dem Namen bekannt sind Population.
Zu diesem Zweck werden numerische und grafische Techniken verwendet, mit denen Informationen dargestellt werden, ohne Vorhersagen oder Rückschlüsse auf die Population zu treffen, aus der sie stammen..

Artikelverzeichnis
- 1 Geschichte
- 1.1 Altertum
- 1.2 Renaissance
- 1.3 Moderne
- 2 Merkmale deskriptiver Statistiken
- 3 Wofür ist beschreibende Statistik??
- 3.1 Wirtschaft
- 3.2 Physik und Mechanik
- 3.3 Medizin
- 3.4 Ernährung
- 4 Beispiele für deskriptive Statistiken
- 4.1 Beispiel 1
- 4.2 Beispiel 2
- 4.3 Beispiel 3
- 5 Grundbegriffe der deskriptiven Statistik
- 5.1 Bevölkerung
- 5.2 Probe
- 5.3 Variable
- 5.4 Maßnahmen der zentralen Tendenz
- 5.5 Dispersionsmessungen
- 6 Themen von Interesse
- 7 Referenzen
Geschichte
Hohes Alter
Die Statistik hat ihren Ursprung in der Notwendigkeit des Menschen, die für sein Überleben und sein Wohlbefinden erforderlichen Informationen zu organisieren und die Ereignisse zu antizipieren, die sie betreffen. Die großen Zivilisationen der Antike hinterließen Aufzeichnungen über Siedler, erhobene Steuern, Erntemengen und die Größe der Armeen.
Zum Beispiel ordnete Ramses II. (1279-1213 v. Chr.) Während seiner langen Regierungszeit eine Volkszählung von Land und Einwohnern in Ägypten an, die bis dahin rund 2 Millionen Einwohner hatte.
Ebenso berichtet die Bibel, dass Mose eine Volkszählung durchgeführt hat, um herauszufinden, wie viele Soldaten die zwölf Stämme Israels hatten.
Auch im antiken Griechenland wurden Menschen und Ressourcen gezählt. Die Römer, die für ihre hohe Organisation bekannt sind, registrierten die Bevölkerung regelmäßig und erstellten alle fünf Jahre Volkszählungen, einschließlich Territorien und Ressourcen..
Renaissance
Nach dem Niedergang Roms waren wichtige statistische Aufzeichnungen bis zur Ankunft der Renaissance rar, als die Statistik als Entscheidungshilfe wieder auftauchte.
Am Ende des 17. Jahrhunderts wurde die Wahrscheinlichkeitstheorie geboren, das Ergebnis der Neigung der Menschen zu Glücksspielen, die der Statistik die mathematische Strenge verlieh, die sie zu einer eigenständigen Wissenschaft machte.
Modernes Alter
Ein neuer Impuls kam mit der Theorie der Fehler und kleinsten Quadrate im 19. Jahrhundert, gefolgt von der Methode der Korrelation zwischen Variablen, um die Beziehung zwischen ihnen quantitativ zu bewerten..
Bis schließlich im 20. Jahrhundert verbreitete sich die Statistik als unverzichtbares Werkzeug zur Lösung von Problemen auf jeden Zweig der Wissenschaft und Technik..
Beschreibende statistische Merkmale
Beschreibende Statistiken zeichnen sich aus durch:
- Organisieren Sie die gesammelten Informationen in Form von Daten und Grafiken. Die Diagramme können vielfältig sein: unter anderem Histogramme, Frequenzpolygone, tortenförmige Diagramme..
- Verteilen Sie die Daten in Frequenzbereichen, um die Verwaltung zu vereinfachen. Verwenden Sie die Arithmetik, um die repräsentativsten Werte der Daten durch Messungen der zentralen Tendenz zu finden und ihre Streuung zu analysieren.
- Bestimmen Sie die Form der Verteilungen, ihre Symmetrie, ob sie zentriert oder schief sind und ob sie spitz oder eher abgeflacht sind.
Wofür ist beschreibende Statistik??
Wann immer Daten gesammelt, organisiert und präsentiert werden müssen, sind deskriptive Statistiken in Bereichen der Wissenschaft, die sich mit vielen Elementen und Mengen befassen, sowie in vielen menschlichen Aktivitäten von entscheidender Bedeutung: Wirtschaft, Politik, Gesundheit, Sport und mehr..
Hier sind einige Beispiele:
Wirtschaft
Deskriptive Statistiken befassen sich mit der konsistenten Erfassung und Organisation von Daten über Bevölkerungsgruppen und deren Alter, Einkommen, Investitionen, Einnahmen und Ausgaben. Auf diese Weise planen Regierungen und Institutionen Verbesserungen und investieren Ressourcen angemessen..
Mit seiner Hilfe werden Einkäufe, Verkäufe, Retouren und die Effizienz von Dienstleistungen überwacht. Aus diesem Grund sind Statistiken für die Entscheidungsfindung unerlässlich.
Physik und Mechanik
Physik und Mechanik verwenden Statistiken, um kontinuierliche Medien zu untersuchen, die aus einer großen Anzahl von Partikeln wie Atomen und Molekülen bestehen. Es stellt sich heraus, dass es nicht möglich ist, jeden von ihnen einzeln zu verfolgen..
Wenn man jedoch das globale Verhalten des Systems (zum Beispiel einen Teil des Gases) unter makroskopischen Gesichtspunkten untersucht, ist es möglich, Durchschnittswerte zu finden und makroskopische Variablen zu definieren, um deren Eigenschaften zu kennen. Ein Beispiel hierfür ist die kinetische Theorie der Gase.
Medizin
Es ist ein wesentliches Instrument bei der Überwachung von Krankheiten, ihrer Entstehung und Entwicklung sowie der Wirksamkeit von Behandlungen.
Statistiken, die Morbiditätsraten, Heilungsraten, Inkubations- oder Entwicklungszeiten einer Krankheit, das Alter, in dem sie normalerweise auftritt, und ähnliche Daten beschreiben, sind für die Entwicklung der wirksamsten Behandlungen erforderlich..
Ernährung
Eine der vielen Anwendungen deskriptiver Statistiken besteht darin, Daten über den Lebensmittelkonsum in verschiedenen Bevölkerungsgruppen aufzuzeichnen und zu bestellen: Quantität, Qualität und die am meisten konsumierten, neben vielen anderen Beobachtungen, die Experten interessieren..
Beschreibende Statistikbeispiele
Im Folgenden finden Sie einige Beispiele, die veranschaulichen, wie nützlich beschreibende Statistik-Tools sind, um Entscheidungen zu treffen:
Beispiel 1

Die Bildungsbehörden eines Landes planen institutionelle Verbesserungen. Angenommen, Sie werden ein neues Schulkantinen-System implementieren.
Dazu sind Daten über die Schülerbevölkerung erforderlich, beispielsweise die Anzahl der Schüler pro Klasse, ihr Alter, Geschlecht, Größe, Gewicht und sozioökonomischer Status. Diese Informationen werden dann in Form von Tabellen und Grafiken dargestellt..
Beispiel 2
Um die lokale Fußballmannschaft im Auge zu behalten und Neuverpflichtungen einzugehen, verfolgen die Manager die Anzahl der gespielten, gewonnenen, unentschieden und verlorenen Spiele sowie die Anzahl der Tore, die Torschützen und die Art und Weise, wie sie ein Tor erzielt haben: Freistoß, Hälfte Gericht, Strafen, mit linkem oder rechtem Bein, unter anderem Details.
Beispiel 3
Eine Eisdiele hat verschiedene Eissorten und möchte ihren Umsatz verbessern. Daher führen die Eigentümer eine Studie durch, in der sie die Anzahl der Kunden zählen und sie nach Geschlecht und Altersgruppe in Gruppen einteilen.
In dieser Studie werden beispielsweise der bevorzugte Eisgeschmack und die meistverkaufte Präsentation aufgezeichnet. Und mit den gesammelten Daten planen sie den Kauf der Aromen sowie der für ihre Zubereitung erforderlichen Behälter und Zubehörteile..
Beschreibende statistische Grundlagen
Diese grundlegenden Konzepte sind notwendig, um statistische Techniken anzuwenden.
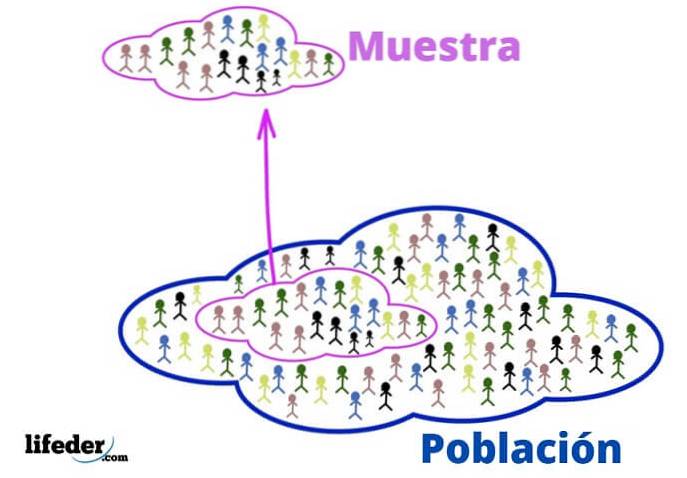
Population
Im statistischen Kontext bezieht sich die Population auf das Universum oder die Gruppe, aus der die Informationen stammen.
Es geht nicht immer um Menschen, da es sich um Gruppen von Tieren, Pflanzen oder Objekten wie Autos, Atomen, Molekülen und sogar um Ereignisse und Ideen handeln kann..
Show
Wenn die Population sehr groß ist, wird eine repräsentative Stichprobe daraus gezogen und analysiert, ohne relevante Informationen zu verlieren..
Sie kann nach dem Zufallsprinzip oder nach bestimmten Kriterien ausgewählt werden, die zuvor vom Analysten festgelegt wurden. Der Vorteil ist, dass es als Teil der Bevölkerung viel leichter zu handhaben ist.
Variable
Es bezieht sich auf die Menge von Werten, die ein bestimmtes Merkmal der Bevölkerung annehmen kann. Eine Studie kann verschiedene Variablen enthalten, z. B. Alter, Geschlecht, Gewicht, akademisches Niveau, Familienstand, Einkommen, Temperatur, Farbe, Zeit und vieles mehr.
Die Variablen können unterschiedlicher Natur sein, daher gibt es Kriterien, um sie zu klassifizieren und ihnen die am besten geeignete Behandlung zu geben.
Kategoriale Variablen und numerische Variablen
Abhängig von der Art und Weise, wie sie gemessen werden, können die Variablen sein:
-Kategorial
-Numerisch
Kategoriale Variablen, auch genannt qualitativ, repräsentieren Eigenschaften wie den Familienstand einer Person, die ledig, verheiratet, geschieden oder verwitwet sein kann.
Stattdessen numerische Variablen oder quantitativ, kann gemessen werden, wie Alter, Zeit, Gewicht, Einkommen und mehr.
Diskrete Variablen und kontinuierliche Variablen
Diskrete Variablen nehmen nur diskrete Werte an, wie der Name schon sagt. Beispiele hierfür sind die Anzahl der Kinder in einer Familie, die Anzahl der Fächer in einem bestimmten Kurs und die Anzahl der Autos auf einem Parkplatz.
Diese Variablen nehmen nicht immer ganzzahlige Werte an, da es auch gebrochene gibt.
Andererseits lassen kontinuierliche Variablen unendliche Werte innerhalb eines bestimmten Bereichs zu, wie z. B. das Gewicht einer Person, den pH-Wert des Blutes, den Zeitpunkt einer telefonischen Konsultation und den Durchmesser von Fußbällen..
Maße der zentralen Tendenz
Sie geben einen Überblick über den allgemeinen Trend, dem die Daten folgen. Wir werden die drei am häufigsten verwendeten zentralen Maßnahmen erwähnen:
-Hälfte
-Median
-Mode
Hälfte
Entspricht dem Durchschnitt der Werte. Es wird berechnet, indem alle Beobachtungen addiert und durch die Gesamtzahl dividiert werden:

Mode
Dies ist der Wert, der in einem Datensatz am häufigsten, am häufigsten oder am häufigsten wiederholt wird, da es in einer Verteilung möglicherweise mehr als einen Modus gibt.
Median
Beim Sortieren eines Datensatzes ist der Median der zentrale Wert aller Daten.
Dispersionsmaße
Sie weisen auf die Variabilität der Daten hin und geben eine Vorstellung davon, wie weit oder verstreut sie von den zentralen Maßnahmen sind. Die am häufigsten verwendeten sind:
Rang
Es ist die Differenz zwischen dem größten Wert xM. und das kleinste xm aus einem Datensatz:
Rang = xM. - xm
Varianz
Misst, wie weit die Daten vom Durchschnittswert entfernt sind. Dazu wird ein Durchschnitt gebildet, jedoch mit den Unterschieden zwischen einem beliebigen Wert xich und der Mittelwert, der quadriert, um zu verhindern, dass sie sich gegenseitig aufheben. Es wird normalerweise mit dem griechischen Buchstaben σ im Quadrat oder mit s bezeichnetzwei::

Die Varianz hat nicht die gleichen Einheiten wie die Daten, daher wird die Standardabweichung als Quadratwurzel der Varianz definiert und als σ oder s bezeichnet:

Anstatt alle Daten einzeln zu berücksichtigen, ist es vorzuziehen, sie in Bereiche zu gruppieren, was die Arbeit erleichtert, insbesondere wenn viele Werte vorhanden sind. Wenn Sie beispielsweise mit Kindern in einer Schule arbeiten, können Sie diese in Altersgruppen einteilen: 0 bis 6 Jahre, 6 bis 12 Jahre und 12 bis 18 Jahre.
Diagramme
Sie bieten eine hervorragende Möglichkeit, die Verteilung der Daten auf einen Blick zu sehen. Sie enthalten alle in den Tabellen und Tabellen gesammelten Informationen, sind jedoch wesentlich günstiger.
Es gibt eine große Vielfalt von ihnen: mit Balken, linear, kreisförmig, Stiel und Blatt, Histogrammen, Frequenzpolygonen und Piktogrammen. Beispiele für statistische Diagramme sind in Abbildung 3 dargestellt..
Themen von Interesse
Zweige der Statistik.
Statistische Variablen.
Bevölkerung und Stichprobe.
Inferenzstatistik.
Verweise
- Faraldo, P. Statistik und Forschungsmethodik. Wiederhergestellt von: eio.usc.es.
- Fernández, S. 2002. Beschreibende Statistik. 2 .. Auflage. ESIC Editorial. Wiederhergestellt von: Google Books.
- Geschichte der Statistik. Wiederhergestellt von: eumed.net.
- Ibañez, P. 2010. Mathematik II. Kompetenzansatz. Lernen einbinden.
- Monroy, S. 2008. Beschreibende Statistik. 1. Auflage. Nationales Polytechnisches Institut von Mexiko.
- Universumsformeln. Beschreibende Statistik. Wiederhergestellt von: universoformulas.com.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.