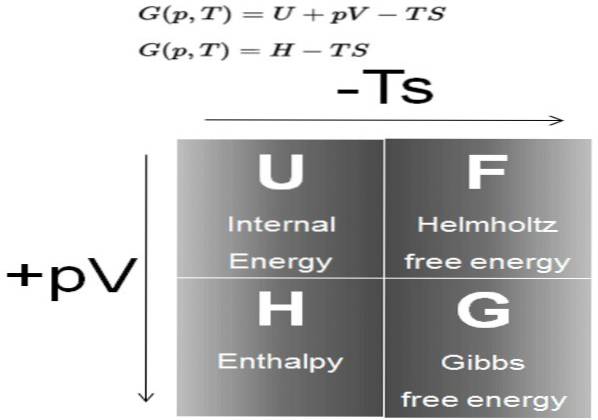
Das Gibbs freie Energie (allgemein als G bezeichnet) ist ein thermodynamisches Potential, das als Differenz der Enthalpie H abzüglich des Produkts der Temperatur T durch die Entropie S des Systems definiert ist:
G = H - T S.
Gibbs freie Energie wird in Joule (nach dem Internationalen System), in Erg (für das Cegesimal System of Units), in Kalorien oder in Elektronenvolt gemessen (für Elektrovolt).
In Prozessen, die bei konstantem Druck und konstanter Temperatur ablaufen, beträgt die Variation der freien Gibbs-Energie ΔG = ΔH - T ΔS. In solchen Prozessen repräsentiert (G) die im System verfügbare Energie, die in Arbeit umgewandelt werden kann.
Beispielsweise nimmt bei exothermen chemischen Reaktionen die Enthalpie ab, während die Entropie zunimmt. In der Gibbs-Funktion wird diesen beiden Faktoren entgegengewirkt, aber nur wenn die Gibbs-Energie abnimmt, tritt die Reaktion spontan auf..
Wenn also die Variation von G negativ ist, ist der Prozess spontan. Wenn die Gibbs-Funktion ihr Minimum erreicht, erreicht das System einen stabilen Gleichgewichtszustand. Zusammenfassend können wir in einem Prozess, bei dem Druck und Temperatur konstant bleiben, Folgendes bestätigen:
- Wenn der Prozess spontan ist, dann ist ΔG < 0
- Wenn sich das System im Gleichgewicht befindet: ΔG = 0
- In einem nicht spontanen Prozess steigt G an: ΔG> 0.
Artikelverzeichnis
Die freie Gibbs-Energie (G) wird unter Verwendung der zu Beginn angegebenen Definition berechnet:
G = H - T⋅S
Die Enthalpie H ist wiederum ein thermodynamisches Potential, definiert als:
H = U + P V.
Als nächstes wird eine schrittweise Analyse durchgeführt, um die unabhängigen Variablen zu kennen, von denen die Gibbs-Energie eine Funktion ist:
1- Aus dem ersten Hauptsatz der Thermodynamik geht hervor, dass die innere Energie U mit der Entropie S des Systems und seinem Volumen V für reversible Prozesse durch die Differentialbeziehung zusammenhängt:
dU = dQ - dW = TdS - PdV
Aus dieser Gleichung folgt, dass die innere Energie U eine Funktion der Variablen S und V ist:
U = U (S, V)
2- Ausgehend von der Definition von H und dem Differential erhalten wir:
dH = dU + d (P V) = dU + VdP + PdV
3- Wenn wir den in (1) erhaltenen Ausdruck für dU einsetzen, haben wir:
dH = TdS - PdV + VdP + PdV = TdS + VdP
Daraus wird geschlossen, dass die Enthalpie H von der Entropie S und dem Druck P abhängt, dh:
H = H (S, P)
4- Nun wird die Gesamtdifferenz der freien Gibbs-Energie berechnet, wobei Folgendes erhalten wird:
dG = dH -TdS -SdT = TdS + VdP -TdS -SdT
Wobei dH durch den in (3) gefundenen Ausdruck ersetzt wurde.
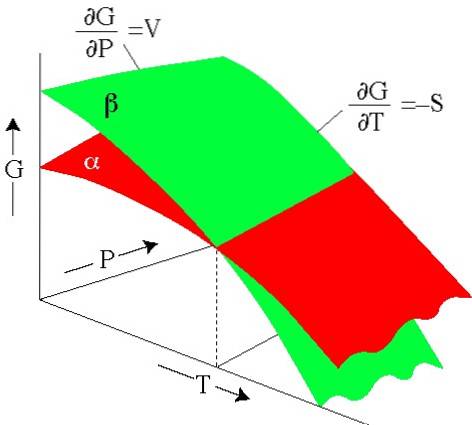
5- Schließlich erhalten wir bei der Vereinfachung: dG = VdP - SdT, klar ist, dass die freie Energie G vom Druck und der Temperatur T abhängt als:
G = G (P, T)
Aus der Analyse im vorherigen Abschnitt folgt, dass die innere Energie eines Systems eine Funktion der Entropie und des Volumens ist:
U = U (S, V)
Dann das Differential von ODER wird sein:
dU = ∂S.U |V. dS + ∂V.U |S. dV = TdS - PdV
Aus diesem partiellen abgeleiteten Ausdruck können die sogenannten Maxwell-thermodynamischen Beziehungen abgeleitet werden. Partielle Ableitungen gelten, wenn eine Funktion von mehr als einer Variablen abhängt und einfach durch Anwendung des Satzes im nächsten Abschnitt berechnet werden kann.
∂V.T |S. = -∂S.P |V.
Um zu dieser Beziehung zu gelangen, muss die Clairaut-Schwarz-Theorem zu partiellen Ableitungen, in denen Folgendes angegeben ist:
"Die gemischten Ableitungen zweiter Ordnung mit den vertauschten Variablen sind gleich, solange die abzuleitenden Funktionen stetig und differenzierbar sind.".
Basierend auf dem, was in Punkt 3 des vorherigen Abschnitts gezeigt wird:
H = H (S, P) und dH = TdS + VdP
Es kann erhalten werden:
∂P.T |S. = ∂S.V |P.
Ähnlich verfahren wir mit Gibbs freier Energie G = G (P, T) und mit Helmholtz freier Energie F = F (T, V) um die anderen beiden thermodynamischen Maxwell-Beziehungen zu erhalten.
1- Assoziiert mit der inneren Energie U: ∂V.T |S. = -∂S.P |V.
2- Die aus der Enthalpie H erhaltene: ∂P.T |S. = ∂S.V |P.
3- Bezogen auf die Helmholtz-Energie F: ∂T.P |V. = ∂V.S |T.
4- Verbunden mit der freien Gibbs-Energie G: ∂T.V |P. = -∂P.S |T.
Berechnen Sie die Variation der freien Gibbs-Energie für 2 Mol ideales Gas bei einer Temperatur von 300 K während einer isothermen Expansion, die das System von einem Anfangsvolumen von 20 Litern auf ein Endvolumen von 40 Litern bringt.
Wir erinnern uns an die Definition von Gibbs freier Energie, die wir haben:
G = H - T S.
Dann ist eine endliche Variation von F:
ΔG = ΔH - T ΔS, da ΔT = 0
In idealen Gasen hängt die Enthalpie nur von ihrer absoluten Temperatur ab. Da es sich jedoch um einen isothermen Prozess handelt, ist ΔH = 0 und ΔG = - T ΔS.
Für ideale Gase beträgt die Entropieänderung eines isothermen Prozesses:
ΔS = nR ln (V.zwei/ V.1)
Was für den Fall dieser Übung gilt, bleibt:
ΔS = 2 Mol × 8,314 J / (K Mol) × 1n (40 l / 20 l) = 11,53 J / K.
Dann können wir die Änderung der Helmholtz-Energie erhalten:
ΔG = –300 K × 11,53 J / K = –3457,70 J..
Unter Berücksichtigung, dass die freie Gibbs-Energie eine Funktion von Temperatur und Druck ist G = G (T, P); Bestimmen Sie die Variation von G während eines Prozesses, bei dem sich die Temperatur für n Mol eines einatomigen idealen Gases nicht ändert (isotherm).
Wie oben gezeigt, hängt die Änderung der Gibbs-Energie nur von der Änderung der Temperatur T und des Volumens V ab, so dass eine infinitesimale Variation davon berechnet wird gemäß:
dG = -SdT + VdP
Wenn es sich jedoch um einen Prozess handelt, bei dem die Temperatur konstant ist, dann ist dF = + VdP, so dass eine endliche Druckänderung ΔP zu einer Änderung der Gibbs-Energie führt, die gegeben ist durch:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = + n R T ln (ΔP)
Unter Verwendung der idealen Gasgleichung:
P V = n R T.
Während eines isothermen Prozesses tritt Folgendes auf:
d (P V) = P dV + V dP = 0
Das ist:
dP / P = - dV / V.
Das obige Ergebnis kann also als Funktion der Lautstärkevariation geschrieben werden ΔV::
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = - ∫ (n R T) dV / V = -n R T ln (ΔV)
Berücksichtigung der folgenden chemischen Reaktion:
N.zwei0 (g) + (3/2) O.zwei (g) ≤ 2NOzwei (g) bei einer Temperatur T = 298 K.
Finden Sie die Variation der freien Gibbs-Energie und geben Sie anhand des erhaltenen Ergebnisses an, ob es sich um einen spontanen Prozess handelt oder nicht.
Hier sind die Schritte:
- Erster Schritt: Reaktionsenthalpien
ΔHr = 2 · ΔH (NOzwei (g)) - ΔH (N.zwei0 (g)) = 2 · 33,2-81,6 = -15,2 kJ / mol
- Zweiter Schritt: die Variation der Reaktionsentropie
ΔSr = 2 · S (NOzwei (g)) - S (N.zwei0 (g)) - (3/2) S (O.zwei (g)) = 2 · 240,1 - 220,1 - 1,5 · 205,2 = -47,7 J / (mol · K).
- Dritter Schritt: Variation der Gibbs-Funktion
Dieser Wert bestimmt das Gleichgewicht zwischen der abnehmenden Energie und der zunehmenden Entropie, um festzustellen, ob die Reaktion schließlich spontan ist oder nicht.
ΔGr = ΔHr - T ΔSr = -15,2 -298 * (-47,7) = -985,4 J / mol
Da es sich um eine negative Variation der Gibbs-Energie handelt, kann geschlossen werden, dass es sich um eine spontane Reaktion bei einer Temperatur von 298 K = 25 ºC handelt.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.