
Kontinuierliche gleichmäßige Verteilungseigenschaften, Beispiele, Anwendungen
Eine Zufallsvariable hat a kontinuierliche gleichmäßige Verteilung wenn die Wahrscheinlichkeit, dass es innerhalb eines endlichen Intervalls [a, b] einen Wert annimmt, für jedes Teilintervall gleicher Länge gleich ist.
Diese Verteilung ist analog zu der diskreten Gleichverteilung, bei der jedem Ergebnis des Zufallsexperiments die gleiche Wahrscheinlichkeit zugewiesen wurde. In diesem Fall ist die zu berücksichtigende Variable jedoch stetig. Beispielsweise folgt das Experiment, bei dem eine reelle Zahl zufällig zwischen den Werten a und b ausgewählt wird, der gleichmäßigen Verteilung. Hier ist seine Grafik:
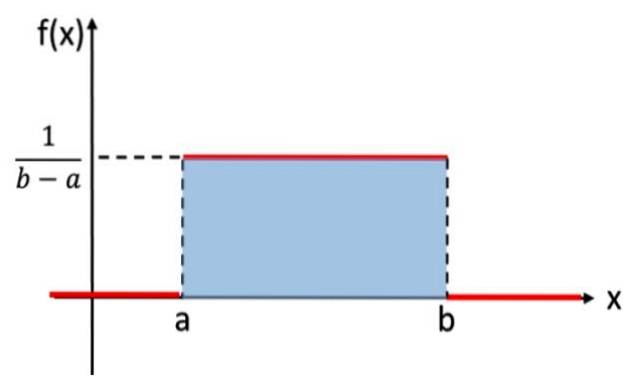
In der mathematischen Notation hat die kontinuierliche Gleichverteilung eine Dichtefunktion, die als stückweise oder stückweise Funktion definiert ist und wie folgt geschrieben werden kann:
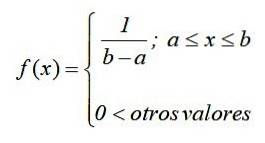
Der Graph dieser Funktion, bekannt als Dichtekurve oder Funktion, ist ein Rechteck, daher ist die kontinuierliche Gleichverteilung auch bekannt als rechteckiges Layout y ist die einfachste der kontinuierlichen Verteilungen.
Die Fläche unter dem Diagramm einer Wahrscheinlichkeitsverteilung ist gleich 1 und nimmt immer positive Werte an. Die gleichmäßige Verteilung erfüllt diese Kriterien. Es ist nicht erforderlich, direkt zu integrieren, um zu überprüfen, ob die Fläche 1 ist, da die Fläche des schattierten Rechtecks in Abbildung 1 mithilfe der folgenden Formel berechnet werden kann:
Fläche = Basis x Höhe = (b - a) x [1 / (b - a)] = 1
Die Kenntnis der Fläche unter der Dichtekurve ist sehr wichtig, da eine Beziehung zwischen der Fläche und der Wahrscheinlichkeit des Auftretens eines Ereignisses besteht, die für diese Verteilung im nächsten Abschnitt bestimmt wird.
Eigenschaften einer kontinuierlichen Gleichverteilung
Die kontinuierliche Gleichverteilung zeichnet sich aus durch:
Dichtefunktion
Sei X die stetige Zufallsvariable, die zum Intervall [a, b] gehört, dann:

Verteilungsfunktion
Die Verteilungsfunktion berechnet die Wahrscheinlichkeit, dass die Zufallsvariable X aus den möglichen Werten des Intervalls [a, b] einen Wert x annimmt. Für eine kontinuierliche Verteilung wird sie im Allgemeinen wie folgt berechnet:

Im Fall der kontinuierlichen Gleichverteilung entspricht die Wahrscheinlichkeit F (x) der Fläche des Rechtecks, dessen Basis (x-a) und dessen Höhe (b-a) ist:

Wenn F (x) = Pr (X = x) ist, wird mathematisch die folgende Funktion gemäß dem vorherigen Ergebnis in Teilen festgelegt:

Auf diese Weise wird überprüft, was zuvor gesagt wurde: Die Wahrscheinlichkeit hängt nur vom Wert von (x-a) ab und nicht von seiner Position im Intervall [a, b]. Das Diagramm der Verteilungsfunktion lautet:
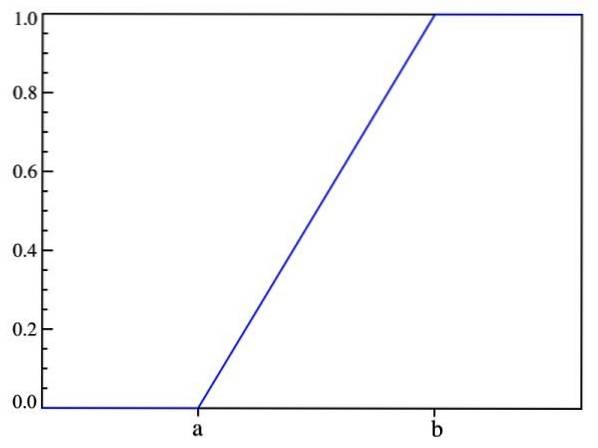
Erwarteter Wert, Varianz und Standardabweichung
Nach zahlreichen Experimenten mit der kontinuierlichen Zufallsvariablen wird ihr Durchschnittswert aufgerufen erwarteter Wert, wird als E (X) bezeichnet und durch das folgende Integral berechnet:

V (X) = E (X.zwei) - EX)zwei
Deshalb:


D (X) = √ V (X)

Median, Modus, Symmetrie und Kurtosis
Es kann leicht überprüft werden, dass der Median, der der zentrale Wert der Gleichverteilung ist, gleich dem Mittelwert ist, und da es keinen Wert gibt, der sich mehr als andere wiederholt, sind alle im Intervall [a, b] gleich wahrscheinlich. Mode gibt es nicht.
In Bezug auf die Symmetrie ist die gleichmäßige Verteilung symmetrisch und die Kurtosis, dh der Grad, in dem sich die Werte um das Zentrum konzentrieren, beträgt -6/5.
Beispiele
Verschiedene Situationen können durch kontinuierliche Verteilung modelliert und somit ihr Verhalten vorhergesagt werden. Hier sind einige Beispiele:
Beispiel 1
Ein Unternehmen, das elektrische Dienstleistungen erbringt, liefert gleichmäßig verteilte Spannungspegel zwischen 123,0 V und 125,0 V. Dies bedeutet, dass in der Haushaltssteckdose jeder Spannungswert erhalten werden kann, der zu diesem Bereich gehört..
Wie oben gezeigt, ist der Graph der Dichtefunktion das Rechteck in Rot:

Die Berechnung der Wahrscheinlichkeit, dass eine Spannung innerhalb des angegebenen Intervalls liegt, ist sehr einfach. Beispielsweise ist die Wahrscheinlichkeit hoch, dass das Unternehmen eine Spannung von weniger als 123,5 V sendet?
Diese Wahrscheinlichkeit entspricht der Fläche des blau schattierten Rechtecks:
P (X.<123.5) = (123.5 −123.0)x 0.5 = 0.25
Und wie hoch ist die Wahrscheinlichkeit, dass die gelieferte Spannung größer als 124,0 V ist??
Da die Gesamtfläche gleich 1 ist, ist die gesuchte Wahrscheinlichkeit:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Dies ist sinnvoll, da 124,0 genau der Wert in der Mitte des Intervalls ist.
Beispiel 2
Eine bestimmte Zufallsvariable X hat eine gleichmäßige Verteilung im Intervall [0,100]. Entscheiden:
a) Die Wahrscheinlichkeit, dass der Wert von X kleiner als 22 ist.
b) Die Wahrscheinlichkeit, dass X Werte zwischen 20 und 35 annimmt.
c) Der erwartete Wert, die Varianz und die Standardabweichung dieser Verteilung.
Antwort auf
Es wird auf ähnliche Weise wie im vorherigen Beispiel bestimmt, aber zuerst müssen wir die Höhe des Rechtecks bestimmen, wobei zu beachten ist, dass die Gesamtfläche gleich 1 sein muss:
Fläche = 100 × Höhe = 1
Daher hat das Rechteck eine Höhe von 1/100 = 0,01
P (X.<22) = 22×0.01 = 0.22
Antwort b
Die angeforderte Wahrscheinlichkeit entspricht der Fläche des Rechtecks mit einer Breite von (35 - 20) und einer Höhe von 0,01:
P (22 Wenn Sie lieber direkt zu der oben angegebenen Verteilungsfunktion wechseln möchten, müssen Sie nur die Werte in ersetzen: P (20 ≤ X ≤ 35) = F (35) -F (20) Mit F (x) gegeben durch: F (x) = (x-a) / (b-a) Die einzugebenden Werte sind: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20 ≤ X ≤ 35) = 0,35-0,20 = 0,15 Der erwartete Wert ist: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 Die Varianz ist: V (X) = (b-a)zwei/ 12 = (100-0)zwei/ 12 = 833,33 Und die Standardabweichung ist: D (X) = 883,33 = 28,87 Diese Verteilung ist nützlich, wenn statistische Simulationsprozesse durchgeführt werden oder wenn an Ereignissen gearbeitet wird, deren Häufigkeit regelmäßig auftritt.. Einige Programmiersprachen erzeugen Zufallszahlen zwischen 0 und 1, und wie aus den vorherigen Beispielen ersichtlich ist, ist die verfolgte Wahrscheinlichkeitsverteilung einheitlich. In diesem Fall beträgt das zu berücksichtigende Intervall [0,1]. Wenn Sie ein Experiment haben, bei dem die Ereignisse, wie zuvor erläutert, regelmäßig sind, können Sie im Prinzip jedem die gleiche Eintrittswahrscheinlichkeit zuweisen. In diesem Fall liefert das Wahrscheinlichkeitsmodell der Gleichverteilung Informationen für die Analyse.. Die gleichmäßige Verteilung wird auch zum Runden der Differenzen zwischen den beobachteten Werten und den realen Werten einer Variablen verwendet, wobei eine gleichmäßige Verteilung des Fehlers in einem gegebenen Intervall gemäß der Rundung angenommen wird, üblicherweise von -0,5 bis +0,5.Antwort c
Anwendungen
Zufallszahlengenerierung
Abtastung beliebiger Verteilungen
Fehler abrunden
Verweise



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.