
Normalverteilungsformel, Eigenschaften, Beispiel, Übung

Das Normalverteilung oder Gaußsche Verteilung ist die Wahrscheinlichkeitsverteilung in einer stetigen Variablen, in der die Wahrscheinlichkeitsdichtefunktion durch eine Exponentialfunktion aus quadratischem und negativem Argument beschrieben wird, die zu einer Glockenform führt.
Der Name der Normalverteilung ergibt sich aus der Tatsache, dass diese Verteilung für die meisten Situationen gilt, in denen eine kontinuierliche Zufallsvariable an einer bestimmten Gruppe oder Population beteiligt ist..
Beispiele, bei denen die Normalverteilung angewendet wird, sind: die Größe von Männern oder Frauen, Variationen im Maß einer bestimmten physischen Größe oder in messbaren psychologischen oder soziologischen Merkmalen wie dem intellektuellen Quotienten oder den Konsumgewohnheiten eines bestimmten Produkts.
Andererseits wird es eine Gaußsche Verteilung oder Gaußsche Glocke genannt, weil es diesem deutschen mathematischen Genie zugeschrieben wird, dass er es entdeckt hat, um den statistischen Fehler astronomischer Messungen im Jahr 1800 zu beschreiben..
Es wird jedoch angegeben, dass diese statistische Verteilung bereits 1733 von einem anderen großen Mathematiker französischer Herkunft wie Abraham de Moivre veröffentlicht wurde.
Artikelverzeichnis
- 1 Formel
- 2 Eigenschaften der Normalverteilung
- 2.1 Konfidenzintervalle
- 3 Anwendungen der Normalverteilung
- 4 Beispiel
- 5 Übung gelöst
- 6 Referenzen
Formel
Zur Normalverteilungsfunktion in der stetigen Variablen x, mit Parametern μ Y. σ es wird bezeichnet mit:
N (x; μ, σ)
und es ist explizit so geschrieben:
N (x; μ, σ) = ∫-∞x f (s; μ, σ) ds
wo f (u; μ, σ) ist die Wahrscheinlichkeitsdichtefunktion:
f (s; μ, σ) = (1 / (σ√ (2π)) Exp (- szwei/ (2σzwei))
Die Konstante, die die Exponentialfunktion in der Wahrscheinlichkeitsdichtefunktion multipliziert, wird als Normalisierungskonstante bezeichnet und wurde so gewählt, dass:
N (+ ∞, μ, σ) = 1
Der vorherige Ausdruck stellt sicher, dass die Wahrscheinlichkeit, dass die Zufallsvariable x liegt zwischen -∞ und + ∞ ist 1, dh 100% Wahrscheinlichkeit.
Parameter μ ist das arithmetische Mittel der stetigen Zufallsvariablen x y σ die Standardabweichung oder Quadratwurzel der Varianz derselben Variablen. Für den Fall, dass μ = 0 Y. σ = 1 Wir haben dann die Standardnormalverteilung oder die typische Normalverteilung:
N (x; μ = 0, σ = 1)
Eigenschaften der Normalverteilung
1- Wenn eine zufällige statistische Variable einer Normalverteilung der Wahrscheinlichkeitsdichte folgt f (s; μ, σ), Die meisten Daten sind um den Mittelwert gruppiert μ und sind so um sie herum verstreut, dass etwas mehr als ⅔ der Daten dazwischen liegen μ - σ Y. μ + σ.
2- Die Standardabweichung σ es ist immer positiv.
3- Die Form der Dichtefunktion F. ähnelt der einer Glocke, weshalb diese Funktion oft als Gaußsche Glocke oder Gaußsche Funktion bezeichnet wird.
4- In einer Gaußschen Verteilung fallen der Mittelwert, der Median und der Modus zusammen.
5- Die Wendepunkte der Wahrscheinlichkeitsdichtefunktion liegen genau bei μ - σ Y. μ + σ.
6- Die Funktion f ist symmetrisch in Bezug auf eine Achse, die ihren Mittelwert durchläuft μ y hat asymptotisch Null für x ⟶ + ∞ und x ⟶ -∞.
7- Je höher der Wert von σ größere Streuung, Rauschen oder Entfernung der Daten um den Mittelwert. Das heißt zu größer σ Die Glockenform ist offener. Stattdessen σ klein zeigt an, dass die Würfel dicht an der Mitte liegen und die Form der Glocke geschlossener oder spitzer ist.
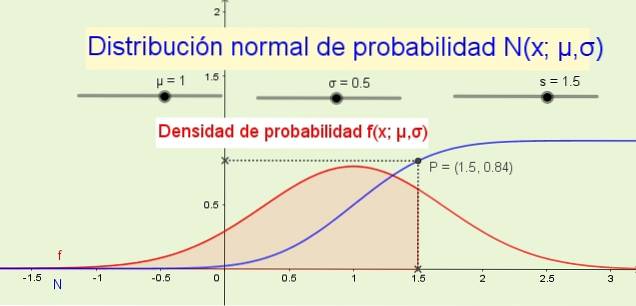
8- Die Verteilungsfunktion N (x; μ, σ) gibt die Wahrscheinlichkeit an, dass die Zufallsvariable kleiner oder gleich ist x. Zum Beispiel in Abbildung 1 (oben) die Wahrscheinlichkeit P, dass die Variable x ist kleiner oder gleich 1,5 ist 84% und entspricht der Fläche unter der Wahrscheinlichkeitsdichtefunktion f (x; μ, σ) von -∞ bis x.
Vertrauensintervalle
9- Wenn die Daten einer Normalverteilung folgen, liegen 68,26% davon dazwischen μ - σ Y. μ + σ.
10- 95,44% der Daten, die einer Normalverteilung folgen, werden zwischen gefunden μ - 2σ Y. μ + 2σ.
11- 99,74% der Daten, die einer Normalverteilung folgen, liegen zwischen μ - 3σ Y. μ + 3σ.
12- Wenn eine Zufallsvariable x Folgen Sie einer Verteilung N (x; μ, σ), dann die Variable
z = (x - μ) / σ folgt der Standardnormalverteilung N (z, 0,1).
Die Änderung der Variablen x zu z Dies wird als Standardisierung oder Typisierung bezeichnet und ist sehr nützlich, wenn die Tabellen der Standardverteilung auf die Daten angewendet werden, die einer nicht standardmäßigen Normalverteilung folgen..
Anwendungen der Normalverteilung
Um die Normalverteilung anzuwenden, muss das Integral der Wahrscheinlichkeitsdichte berechnet werden, was aus analytischer Sicht nicht einfach ist und es nicht immer ein Computerprogramm gibt, das seine numerische Berechnung ermöglicht. Zu diesem Zweck werden die Tabellen mit normalisierten oder standardisierten Werten verwendet, was im vorliegenden Fall nichts anderes als die Normalverteilung ist μ = 0 und σ = 1.
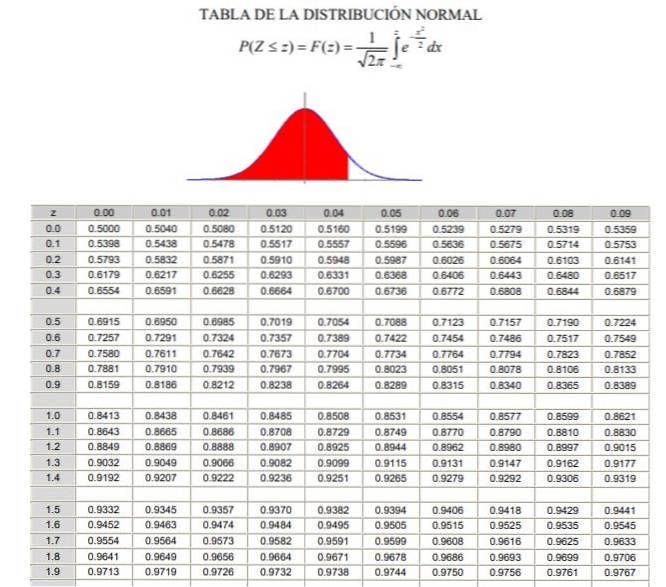
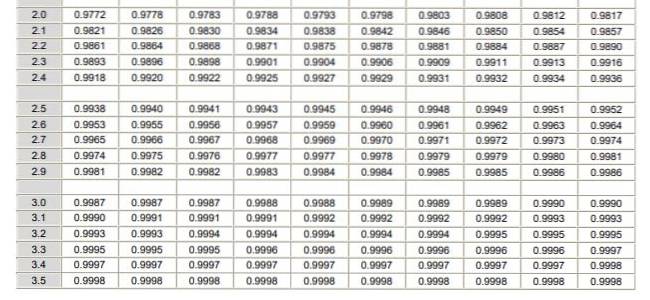
Es ist zu beachten, dass diese Tabellen keine negativen Werte enthalten. Unter Verwendung der Symmetrieeigenschaften der Gaußschen Wahrscheinlichkeitsdichtefunktion können jedoch die entsprechenden Werte erhalten werden. In der unten gezeigten gelösten Übung wird die Verwendung der Tabelle in diesen Fällen angezeigt.
Beispiel
Angenommen, Sie haben eine Reihe von Zufallsdaten x, die einer Normalverteilung von Mittelwert 10 und Standardabweichung 2 folgen. Sie werden gebeten, die Wahrscheinlichkeit zu ermitteln, dass:
a) Die Zufallsvariable x ist kleiner oder gleich 8.
b) kleiner oder gleich 10 ist.
c) Dass die Variable x unter 12 liegt.
d) Die Wahrscheinlichkeit, dass ein Wert x zwischen 8 und 12 liegt.
Lösung:
a) Um die erste Frage zu beantworten, müssen Sie einfach berechnen:
N (x; μ, σ)
Mit x = 8, μ = 10 Y. σ = 2. Wir erkennen, dass es ein Integral ist, das keine analytische Lösung in Elementarfunktionen hat, aber die Lösung wird als Funktion der Fehlerfunktion ausgedrückt erf (x).
Andererseits besteht die Möglichkeit, das Integral in numerischer Form zu lösen, wie es viele Taschenrechner, Tabellenkalkulationen und Computerprogramme wie GeoGebra tun. Die folgende Abbildung zeigt die numerische Lösung für den ersten Fall:
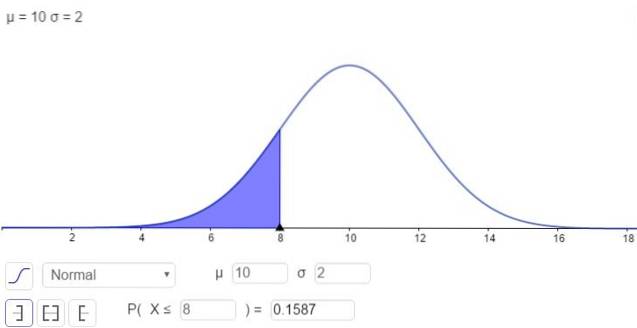
und die Antwort ist, dass die Wahrscheinlichkeit, dass x unter 8 liegt, ist:
P (x ≤ 8) = N (x = 8; μ = 10, σ = 2) = 0,1587
b) In diesem Fall versuchen wir, die Wahrscheinlichkeit zu ermitteln, dass die Zufallsvariable x unter dem Mittelwert liegt, der in diesem Fall 10 wert ist. Die Antwort erfordert keine Berechnung, da wir wissen, dass die Hälfte der Daten unterdurchschnittlich ist und die andere Hälfte überdurchschnittlich. Daher lautet die Antwort:
P (x ≤ 10) = N (x = 10; μ = 10, σ = 2) = 0,5
c) Um diese Frage zu beantworten, müssen Sie berechnen N (x = 12; μ = 10, σ = 2), Dies kann mit einem Taschenrechner mit statistischen Funktionen oder über eine Software wie GeoGebra erfolgen:
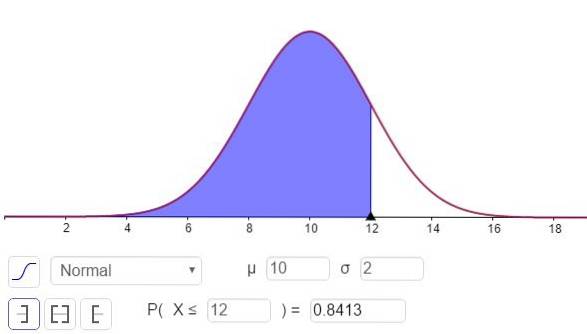
Die Antwort auf Teil c ist in Abbildung 3 zu sehen und lautet:
P (x ≤ 12) = N (x = 12; μ = 10, σ = 2) = 0,8413.
d) Um die Wahrscheinlichkeit zu ermitteln, dass die Zufallsvariable x zwischen 8 und 12 liegt, können wir die Ergebnisse der Teile a und c wie folgt verwenden:
P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26%.
Übung gelöst
Der Durchschnittskurs der Aktien eines Unternehmens beträgt 25 USD mit einer Standardabweichung von 4 USD. Bestimmen Sie die Wahrscheinlichkeit, dass:
a) Eine Aktion kostet weniger als 20 US-Dollar.
b) Das kostet mehr als 30 US-Dollar.
c) Der Preis liegt zwischen 20 und 30 US-Dollar.
Verwenden Sie Standard-Normalverteilungstabellen, um Antworten zu finden.
Lösung:
Um die Tabellen verwenden zu können, muss an die normalisierte oder typisierte z-Variable übergeben werden:
$ 20 in der normalisierten Variablen sind gleich z = (20 $ - 25 $) / $ 4 = -5/4 = -1,25 und
30 US-Dollar in der normalisierten Variablen sind gleich z = (30 $ - 25 $) / $ 4 = +5/4 = +1,25.
a) $ 20 entspricht -1,25 in der normalisierten Variablen, aber die Tabelle hat keine negativen Werte, daher setzen wir den Wert +1,25, was den Wert von 0,8944 ergibt.
Wenn 0,5 von diesem Wert subtrahiert wird, ist das Ergebnis die Fläche zwischen 0 und 1,25, die übrigens (symmetrisch) mit der Fläche zwischen -1,25 und 0 identisch ist. Das Ergebnis der Subtraktion ist 0,8944 - 0,5 = 0,3944 Das ist der Bereich zwischen -1,25 und 0.
Interessant ist jedoch der Bereich von -∞ bis -1,25, der 0,5 - 0,3944 = 0,1056 beträgt. Es wird daher der Schluss gezogen, dass die Wahrscheinlichkeit, dass eine Aktie unter 20 USD liegt, 10,56% beträgt.
b) $ 30 in der typisierten Variablen z ist 1,25. Für diesen Wert erscheint in der Tabelle die Zahl 0,8944, die dem Bereich von -∞ bis +1,25 entspricht. Die Fläche zwischen +1,25 und + ∞ beträgt (1 - 0,8944) = 0,1056. Das heißt, die Wahrscheinlichkeit, dass eine Aktie mehr als 30 USD kostet, beträgt 10,56%.
c) Die Wahrscheinlichkeit, dass eine Aktion Kosten zwischen 20 und 30 US-Dollar verursacht, wird wie folgt berechnet:
100% -10,56% - 10,56% = 78,88%
Verweise
- Statistik und Wahrscheinlichkeit. Normalverteilung. Wiederhergestellt von: projectdescartes.org
- Geogebra. Klassische Geogebra, Wahrscheinlichkeitsrechnung. Von geogebra.org wiederhergestellt
- MathWorks. Gaußsche Verteilung. Wiederhergestellt von: es.mathworks.com
- Mendenhall, W. 1981. Statistik für Management und Wirtschaft. 3 .. Auflage. Grupo Editorial Iberoamérica.
- Stat Trek. Bringen Sie sich Statistik bei. Poisson-Verteilung. Wiederhergestellt von: stattrek.com,
- Triola, M. 2012. Elementare Statistik. 11 .. Ed. Pearson Education.
- Universität von Vigo. Kontinuierliche Hauptverteilungen. Wiederhergestellt von: anapg.webs.uvigo.es
- Wikipedia. Normalverteilung. Wiederhergestellt von: es.wikipedia.org


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.