
Durchmessersymbole und Formeln, wie man es bekommt, Umfang
Das Durchmesser Es ist die gerade Linie, die durch die Mitte einer geschlossenen flachen Kurve oder einer Figur in zwei oder drei Dimensionen verläuft und die auch ihre gegenüberliegenden Punkte verbindet. Normalerweise ist es ein Umfang (eine flache Kurve), ein Kreis (eine flache Figur), eine Kugel oder ein rechter Kreiszylinder (dreidimensionale Objekte)..
Obwohl Umfang und Kreis normalerweise als Synonyme verwendet werden, gibt es einen Unterschied zwischen den beiden Begriffen. Der Umfang ist die geschlossene Kurve, die den Kreis umschließt und die Bedingung erfüllt, dass der Abstand zwischen einem seiner Punkte und dem Mittelpunkt gleich ist. Dieser Abstand ist nichts anderes als der Radius des Umfangs. Stattdessen ist der Kreis eine ebene Figur, die durch den Umfang begrenzt wird.

Bei Umfang, Kreis und Kugel ist der Durchmesser ein gerades Segment, das mindestens drei Punkte enthält: den Mittelpunkt plus zwei Punkte der Kante des Umfangs oder Kreises oder die Oberfläche der Kugel.
Und für den rechten Kreiszylinder bezieht sich der Durchmesser auf den Querschnitt, der zusammen mit der Höhe die beiden charakteristischen Parameter darstellt.
Der Durchmesser des Umfangs und des Kreises, symbolisiert durch ø oder einfach den Buchstaben „D“ oder „d“, hängt mit seinem Umfang, seiner Kontur oder Länge zusammen, der mit dem Buchstaben L bezeichnet wird:
L = π.D = π. oder
Solange es einen Umfang gibt, ist der Quotient zwischen seiner Länge und seinem Durchmesser die irrationale Zahl π = 3.14159… auf folgende Weise:
π = L / D.
Artikelverzeichnis
- 1 So erhalten Sie den Durchmesser?
- 1.1 Figuren konstanter Breite
- 2 Durchmesser eines Kreises
- 2.1 - Beispiel 1
- 2.2 - Beispiel 2
- 3 Wie viele Durchmesser hat ein Umfang??
- 4 Referenzen
So erhalten Sie den Durchmesser?
Wenn Sie den Umfang oder den Kreis oder direkt das kreisförmige Objekt wie eine Münze oder einen Ring zeichnen, ist es sehr einfach, den Durchmesser mit einem Lineal zu ermitteln. Sie müssen nur sicherstellen, dass die Kante des Lineals gleichzeitig zwei Punkte am Umfang und in der Mitte berührt..
Ein Messschieber, Nonius oder Messschieber eignet sich sehr gut zum Messen von Außen- und Innendurchmessern an Münzen, Reifen, Ringen, Muttern, Rohren und mehr..

Wenn anstelle des Objekts oder seiner Zeichnung Daten wie der Radius vorhanden sind R., dann multiplizieren wir mit 2 haben wir den Durchmesser. Und wenn die Länge oder der Umfang des Umfangs bekannt ist, kann der Durchmesser auch durch Löschen bekannt gemacht werden:
D = 2.R.
D = L / π
Eine andere Möglichkeit, den Durchmesser zu ermitteln, besteht darin, die Fläche des Kreises, die sphärische Oberfläche, den Querschnitt des Zylinders, die gekrümmte Fläche des Zylinders oder die Volumina der Kugel oder des Zylinders zu kennen. Es hängt alles davon ab, um welche geometrische Figur es sich handelt. Zum Beispiel ist der Durchmesser in den folgenden Bereichen und Volumina beteiligt:
-Kreisfläche: π. (D / 2)zwei
-Sphärische Oberfläche: 4π. (D / 2)zwei
-Volumen der Kugel: (4/3) π. (D / 2)3
-Rechtes Kreiszylindervolumen: π. (D / 2)zwei.H (H ist die Höhe des Zylinders)
Zahlen mit konstanter Breite
Der Kreis ist eine flache Figur mit konstanter Breite, da die Breite, wo immer Sie ihn betrachten, der Durchmesser D ist. Es gibt jedoch auch andere, vielleicht weniger bekannte Figuren, deren Breite ebenfalls konstant ist..
Lassen Sie uns zunächst sehen, was unter der Breite einer Figur zu verstehen ist: Es ist der Abstand zwischen zwei parallelen Linien - Stützlinien -, die wiederum senkrecht zur angegebenen Richtung sind und die Figur einschließen, wie im linken Bild gezeigt:
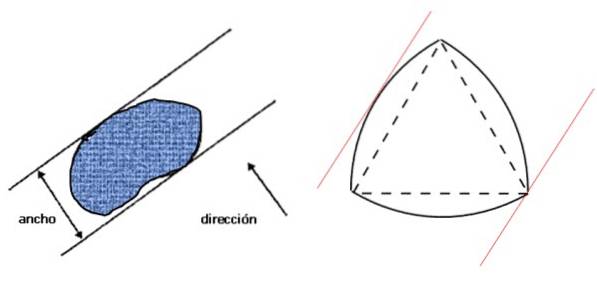
Rechts daneben befindet sich das Reuleaux-Dreieck, eine Figur mit konstanter Breite, die die in der linken Figur angegebene Bedingung erfüllt. Wenn die Breite der Figur D ist, ist ihr Umfang durch den Satz von Barbier gegeben:
L = π.D
Die Abwasserkanäle der kalifornischen Stadt San Francisco sind wie ein Reuleaux-Dreieck geformt, benannt nach dem deutschen Ingenieur Franz Reuleaux (1829 - 1905). Auf diese Weise können die Abdeckungen nicht durch das Loch fallen und es wird weniger Material verwendet, um sie herzustellen, da ihre Fläche kleiner als die des Kreises ist:
A = (1- √3) .πDzwei = 0,705.Dzwei
Während für einen Kreis:
A = π (D / 2)zwei = (π / 4) D.zwei= 0,785.Dzwei
Dieses Dreieck ist jedoch nicht die einzige Figur mit konstanter Breite. Sie können das sogenannte bauen Reuleaux-Polygone mit anderen Polygonen, die eine ungerade Anzahl von Seiten haben.
Durchmesser eines Umfangs

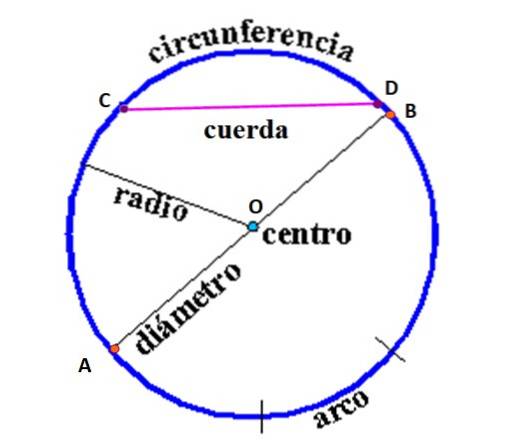
In der nächsten Abbildung sind die Elemente des Umfangs wie folgt definiert:
String: Liniensegment, das zwei Punkte am Umfang verbindet. In der Abbildung ist der Akkord dargestellt, der die Punkte C und D verbindet. Es können jedoch unendlich viele Akkorde gezeichnet werden, die ein beliebiges Punktpaar auf dem Umfang verbinden.
Durchmesser: Es ist der Akkord, der durch die Mitte verläuft und zwei Punkte des Umfangs mit der Mitte O verbindet. Es ist der längste Akkord eines Umfangs, aus diesem Grund wird er "Dur-Akkord" genannt..
Radio: Liniensegment, das die Mitte mit einem beliebigen Punkt auf dem Umfang verbindet. Sein Wert ist ebenso wie der Durchmesser konstant.
Umfang: ist die Menge aller Punkte in gleichem Abstand von O..
Bogen: definiert als ein Umfangssegment, das durch zwei Radien begrenzt ist (in der Figur nicht gezeichnet).
- Beispiel 1
Das gezeigte Rechteck ist 10 Zoll groß und bildet beim Rollen einen rechten Kreiszylinder mit einem Durchmesser von 5 Zoll. Beantworten Sie folgende Fragen:
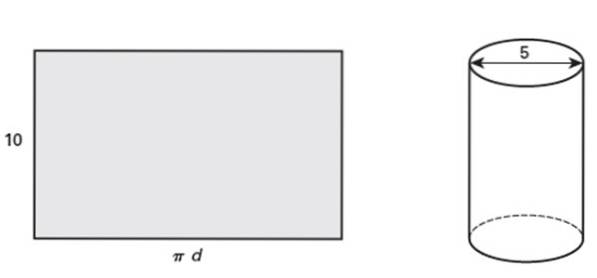
a) Wie ist die Kontur des Rohrs??
b) Finden Sie den Bereich des Rechtecks
c) Berechnen Sie die Querschnittsfläche des Zylinders.
Lösung für
Der Umriss der Röhre ist L = π.D = 5π in = 15,71 in.
Lösung b
Die Fläche des Rechtecks ist Basis x Höhe, Da die Basis L bereits berechnet wurde und die Höhe laut Aussage 10 Zoll beträgt, gilt Folgendes:
A = 15,71 Zoll x 10 Zoll = 157,1 Zollzwei.
Lösung c
Schließlich wird die angeforderte Fläche wie folgt berechnet:
A = π (D / 2)zwei = (π / 4) D.zwei = (π / 4) x (5 Zoll)zwei= 19,63 Zollzwei.
- Beispiel 2
Berechnen Sie den schattierten Bereich in Abbildung 5a. Das Quadrat hat Seite L..
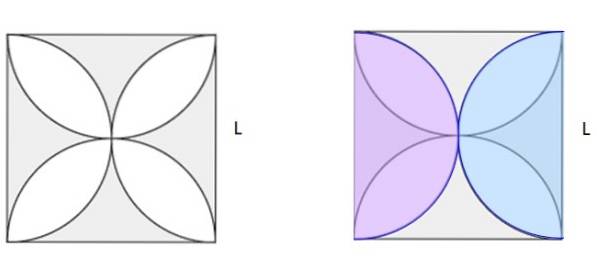
Lösung
In Abbildung 5b wurden zwei Halbkreise gleicher Größe in Pink und Blau gezeichnet, die der Originalfigur überlagert sind. Zwischen ihnen bilden sie einen vollständigen Kreis. Wenn Sie die Fläche des Quadrats finden und die Fläche des Kreises subtrahieren, machen Sie die schattierte Fläche in Abbildung 5b. Bei genauerem Hinsehen stellt sich heraus, dass es sich bei 5a um die Hälfte des schattierten Bereichs handelt.
-Quadratische Fläche: L.zwei
-Halbkreisdurchmesser: L.
-Kreisfläche: π. (L / 2)zwei= (π / 4) L.zwei
-Flächendifferenz = Hälfte der schattierten Fläche =
L.zwei - (π / 4) L.zwei = [(4 - π) / 4] L.zwei= 0,2146 lzwei
-Schattierte Fläche = 2 x 0,2146 lzwei= 0,4292L2
Wie viele Durchmesser hat ein Umfang??
Auf einem Umfang können unendliche Durchmesser gezeichnet werden, von denen jeder den gleichen Wert hat.
Verweise
- Antonio. Reuleaux-Dreiecke und andere Kurven konstanter Breite. Wiederhergestellt von: divulgators.com.
- Baldor, A. 2002. Ebenen- und Raumgeometrie und Trigonometrie. Patria Kulturgruppe.
- Jiménez, R. Mathematik II. Geometrie und Trigonometrie. 2 .. Auflage. Pearson.
- Wikipedia. Reuleaux-Dreieck. Wiederhergestellt von: es.wikipedia.org.
- Wolfram MathWorld. Durchmesser. Wiederhergestellt von: mathworld.wolfram.com.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.