
Unterschied zwischen einem gemeinsamen Bruch und einer Dezimalzahl
Zu identifizieren Was ist der Unterschied zwischen einem gemeinsamen Bruch und einer Dezimalzahl? es reicht aus, beide Elemente zu beobachten: eines repräsentiert eine rationale Zahl, und das andere enthält in seiner Konstitution einen ganzen Teil und einen dezimalen Teil.
Ein "gemeinsamer Bruch" ist der Ausdruck einer Menge geteilt durch eine andere, ohne diese Teilung durchzuführen. Mathematisch gesehen ist ein gemeinsamer Bruch eine rationale Zahl, die als Quotient aus zwei ganzen Zahlen „a / b“ definiert ist, wobei b ≠ 0 ist.

Eine "Dezimalzahl" ist eine Zahl, die aus zwei Teilen besteht: einem ganzzahligen Teil und einem Dezimalteil..
Um den ganzzahligen Teil vom Dezimalteil zu trennen, wird ein Komma gesetzt, das als Dezimalpunkt bezeichnet wird. Abhängig von der Bibliographie wird jedoch auch ein Punkt verwendet.
Dezimal Zahlen
Eine Dezimalzahl kann eine endliche oder unendliche Anzahl von Zahlen in ihrem Dezimalteil haben. Die unendliche Anzahl von Dezimalstellen kann auch in zwei Typen zerlegt werden:
Periodisch
Das heißt, es hat ein sich wiederholendes Muster. Zum Beispiel 2.454545454545…
Nicht periodisch
Sie haben kein sich wiederholendes Muster. Zum Beispiel 1.7845265397219…
Zahlen mit einer periodischen unendlichen oder unendlichen Anzahl von Dezimalstellen werden als rationale Zahlen bezeichnet, während Zahlen mit einer nicht periodischen unendlichen Zahl als irrational bezeichnet werden.
Die Vereinigung der Menge rationaler Zahlen und der Menge irrationaler Zahlen wird als Menge reeller Zahlen bezeichnet.

Unterschiede zwischen gemeinsamem Bruch und Dezimalzahl
Die Unterschiede zwischen einem gemeinsamen Bruch und einer Dezimalzahl sind:
1- Dezimalteil
Jeder gemeinsame Bruch hat eine endliche Anzahl von Zahlen in seinem Dezimalteil oder eine unendliche periodische Zahl, während eine Dezimalzahl eine unendliche nichtperiodische Anzahl von Zahlen in ihrem Dezimalteil haben kann..
Das Obige besagt, dass jede rationale Zahl (jeder gemeinsame Bruch) eine Dezimalzahl ist, aber nicht jede Dezimalzahl eine rationale Zahl (ein gemeinsamer Bruch)..
2- Notation
Jeder gemeinsame Bruch wird als Quotient aus zwei ganzen Zahlen bezeichnet, während eine irrationale Dezimalzahl auf diese Weise nicht bezeichnet werden kann..
Die in der Mathematik am häufigsten verwendeten irrationalen Dezimalzahlen werden durch Quadratwurzeln bezeichnet (√ ), kubisch (³√ ) und höhere Noten.
Daneben gibt es zwei sehr berühmte Zahlen, nämlich die mit e bezeichnete Eulernummer; und die mit pi bezeichnete Zahl pi.

So wechseln Sie von einem gemeinsamen Bruch zu einer Dezimalzahl?
Um von einem gemeinsamen Bruch zu einer Dezimalzahl zu gelangen, machen Sie einfach die entsprechende Division. Wenn Sie beispielsweise 3/4 haben, beträgt die entsprechende Dezimalzahl 0,75.
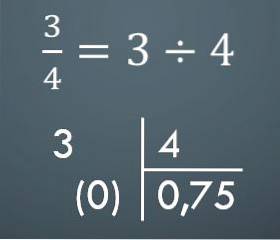
Wie man von einer rationalen Dezimalzahl zu einem gemeinsamen Bruch übergeht?
Der umgekehrte Vorgang zum vorherigen kann ebenfalls durchgeführt werden. Das folgende Beispiel zeigt eine Technik zum Übergang von einer rationalen Dezimalzahl zu einem gemeinsamen Bruch:
- Sei x = 1,78
Da x zwei Dezimalstellen hat, wird die vorherige Gleichheit mit 10² = 100 multipliziert, womit wir 100x = 178 erhalten; und das Auflösen nach x ergibt x = 178/100. Dieser letzte Ausdruck ist der gemeinsame Bruch, der die Zahl 1,78 darstellt.
Aber kann dieser Vorgang für Zahlen mit einer periodischen unendlichen Anzahl von Dezimalstellen durchgeführt werden? Die Antwort lautet Ja, und das folgende Beispiel zeigt die folgenden Schritte:
- Sei x = 2.193193193193…
Da die Periode dieser Dezimalzahl 3 Stellen (193) hat, wird der vorherige Ausdruck mit 10³ = 1000 multipliziert, womit wir den Ausdruck 1000x = 2193.193193193193 erhalten ... .
Jetzt wird der letzte Ausdruck vom ersten subtrahiert und der gesamte Dezimalteil wird gelöscht, wobei der Ausdruck 999x = 2191 übrig bleibt, aus dem wir erhalten, dass der gemeinsame Bruch x = 2191/999 ist.
Verweise
- Anderson, J. G. (1983). Technischer Shop Mathematik (Illustrierte Ausgabe). Industrial Press Inc..
- Avendaño, J. (1884). Vollständiges Handbuch für Grundschul- und Grundschulunterricht: für angehende Lehrer und insbesondere für Schüler der normalen Schulen der Provinz (2 ed., Vol. 1). Druck von D. Dionisio Hidalgo.
- Coates, G. und. (1833). Die argentinische Arithmetik: Vollständige Abhandlung über die praktische Arithmetik. Für die Nutzung von Schulen. Drucken des Staates.
- Vom Meer. (1962). Mathe für den Workshop. Reverte.
- DeVore, R. (2004). Praktische Probleme in der Mathematik für Heiz- und Kühltechniker (Illustrierte Ausgabe). Lernen einbinden.
- Jariez, J. (1859). Kompletter Kurs der physikalischen und mechanischen mathematischen Wissenschaften in der industriellen Kunst (2. Aufl.). Eisenbahndruckerei.
- Palmer, C. I. & Bibb, S. F. (1979). Praktische Mathematik: Arithmetik, Algebra, Geometrie, Trigonometrie und Rechenschieber (Nachdruck ed.). Reverte.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.