
Demonstration der Dreiecksungleichheit, Beispiele, gelöste Übungen
Es wird genannt Dreiecksungleichung auf die Eigenschaft zweier reeller Zahlen, die darin bestehen, dass der Absolutwert ihrer Summe immer kleiner oder gleich der Summe ihrer Absolutwerte ist. Diese Eigenschaft wird auch als Minkowski-Ungleichung oder dreieckige Ungleichung bezeichnet.
Diese Eigenschaft von Zahlen wird als dreieckige Ungleichung bezeichnet, da in Dreiecken die Länge einer Seite immer kleiner oder gleich der Summe der beiden anderen ist, obwohl diese Ungleichung nicht immer im Bereich der Dreiecke gilt..

Es gibt mehrere Beweise für die dreieckige Ungleichung in reellen Zahlen, aber in diesem Fall wählen wir einen basierend auf den Eigenschaften des Absolutwerts und des Binomialquadrats.
Satz: Für jedes Zahlenpaar zu Y. b in Bezug auf die reellen Zahlen muss es:
| a + b | ≤ | zu | + | b |
Artikelverzeichnis
- 1 Demo
- 2 Beispiele
- 2.1 Beispiel 1
- 2.2 Beispiel 2
- 2.3 Beispiel 3
- 2.4 Beispiel 4
- 2.5 Beispiel 5
- 2.6 Beispiel 6
- 3 Gelöste Übungen
- 3.1 Übung 1
- 3.2 Übung 2
- 3.3 Übung 3
- 3.4 Übung 4
- 4 Referenzen
Demonstration
Wir beginnen mit der Betrachtung des ersten Mitglieds der Ungleichung, das quadriert wird:
| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (Gleichung 1)
Im vorherigen Schritt haben wir die Eigenschaft verwendet, dass jede quadratische Zahl gleich dem absoluten Wert dieser quadrierten Zahl ist, d. H. | x | ^ 2 = x ^ 2. Die Entwicklung des quadratischen Binomials wurde ebenfalls genutzt.
Alle Nummer x ist kleiner oder gleich seinem absoluten Wert. Wenn die Zahl positiv ist, ist sie gleich, aber wenn die Zahl negativ ist, ist sie immer kleiner als eine positive Zahl. In diesem Fall seinen eigenen absoluten Wert, das heißt, es kann gesagt werden, dass x ≤ | x |.
Das Produkt (a b) ist eine Zahl, daher gilt, dass (a b) ≤ | a b |. Wenn diese Eigenschaft auf (Gleichung 1) angewendet wird, haben wir:
| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | a b | + b ^ 2 (Gleichung 2)
Berücksichtigt man das | a b | = | a || b | (Gleichung 2) kann wie folgt geschrieben werden:
| a + b | ^ 2 ≤ a ^ 2 + 2 | a || b | + b ^ 2 (Gleichung 3)
Da wir jedoch zuvor gesagt haben, dass das Quadrat einer Zahl gleich dem absoluten Wert der Zahl im Quadrat ist, kann Gleichung 3 wie folgt umgeschrieben werden:
| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (Gleichung 4)
Im zweiten Mitglied der Ungleichung wird ein bemerkenswertes Produkt erkannt, das bei Anwendung zu Folgendem führt:
| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (Gleichung 5)
Im vorherigen Ausdruck ist zu beachten, dass die in beiden Gliedern der Ungleichung zu quadrierenden Werte positiv sind, daher muss auch Folgendes erfüllt sein:
| a + b | ≤ (| a | + | b |) (Gleichung 6)
Der obige Ausdruck ist genau das, was demonstrieren wollte.
Beispiele
Als nächstes werden wir die dreieckige Ungleichung anhand mehrerer Beispiele überprüfen.
Beispiel 1
Wir nehmen den Wert a = 2 und den Wert b = 5, dh beide positive Zahlen, und prüfen, ob die Ungleichung erfüllt ist oder nicht.
| 2 + 5 | ≤ | 2 | + | 5 |
| 7 | ≤ | 2 | + | 5 |
7 ≤ 2+ 5
Die Gleichheit wird verifiziert, daher wurde der Satz der Dreiecksungleichheit erfüllt.
Beispiel 2
Die folgenden Werte werden a = 2 und b = -5 gewählt, dh eine positive Zahl und die andere negative, wir prüfen, ob die Ungleichung erfüllt ist oder nicht.
| 2 - 5 | ≤ | 2 | + | -5 |
| -3 | ≤ | 2 | + | -5 |
3 ≤ 2 + 5
Die Ungleichung ist erfüllt, daher wurde der Satz der dreieckigen Ungleichung verifiziert.
Beispiel 3
Wir nehmen den Wert a = -2 und den Wert b = 5, dh eine negative Zahl und den anderen positiven, wir prüfen, ob die Ungleichung erfüllt ist oder nicht.
| -2 + 5 | ≤ | -2 | + | 5 |
| 3 | ≤ | -2 | + | 5 |
3 ≤ 2 + 5
Die Ungleichung wird verifiziert, daher wurde der Satz erfüllt.
Beispiel 4
Die folgenden Werte werden a = -2 und b = -5 gewählt, dh beide negative Zahlen, und wir prüfen, ob die Ungleichung erfüllt ist oder nicht.
| -2 - 5 | ≤ | -2 | + | -5 |
| -7 | ≤ | -2 | + | -5 |
7 ≤ 2+ 5
Die Gleichheit wird verifiziert, daher wurde Minkowskis Ungleichheitssatz erfüllt.
Beispiel 5
Wir nehmen den Wert a = 0 und den Wert b = 5, dh eine Zahl Null und die andere positive, dann prüfen wir, ob die Ungleichung erfüllt ist oder nicht.
| 0 + 5 | ≤ | 0 | + | 5 |
| 5 | ≤ | 0 | + | 5 |
5 ≤ 0+ 5
Die Gleichheit ist erfüllt, daher wurde der Satz der Dreiecksungleichheit verifiziert.
Beispiel 6
Wir nehmen den Wert a = 0 und den Wert b = -7, dh eine Zahl Null und die andere positive, dann prüfen wir, ob die Ungleichung erfüllt ist oder nicht.
| 0 - 7 | ≤ | 0 | + | -7 |
| -7 | ≤ | 0 | + | -7 |
7 ≤ 0+ 7
Die Gleichheit wird verifiziert, daher wurde der Satz der dreieckigen Ungleichheit erfüllt.
Gelöste Übungen
Stellen Sie in den folgenden Übungen geometrisch die Dreiecksungleichung oder Minkowski-Ungleichung für die Zahlen a und b dar.
Die Zahl a wird als Segment auf der X-Achse dargestellt, ihr Ursprung O fällt mit der Null der X-Achse zusammen und das andere Ende des Segments (am Punkt P) befindet sich in der positiven Richtung (rechts) der X-Achse, wenn a> 0, aber wenn a < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
In ähnlicher Weise wird die Zahl b als ein Segment dargestellt, dessen Ursprung auf Punkt P liegt. Das andere Extrem, dh Punkt Q, befindet sich rechts von P, wenn b positiv ist (b> 0) und Punkt Q | b ist | Einheiten links von P, wenn b<0.
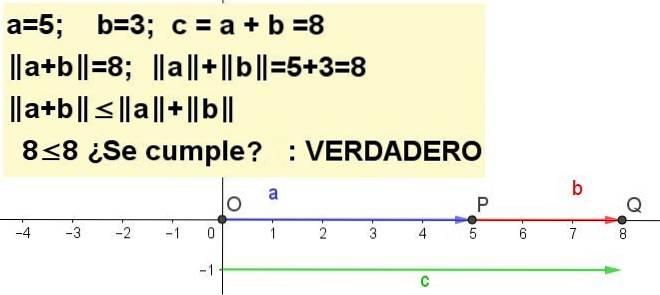
Übung 1
Stellen Sie die Dreiecksungleichung für a = 5 und b = 3 grafisch dar | a + b | ≤ | zu | + | b |, Sein c = a + b.
Übung 2
Stellen Sie die dreieckige Ungleichung für a = 5 und b = -3 grafisch dar.
| a + b | ≤ | zu | + | b |, Sein c = a + b.

Übung 3
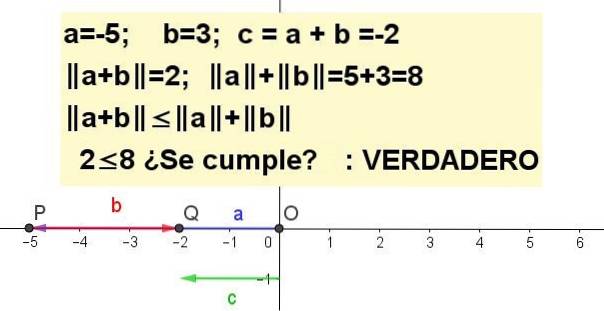
Zeigen Sie grafisch die Dreiecksungleichung für a = -5 und b = 3.
| a + b | ≤ | zu | + | b |, Sein c = a + b.
Übung 4
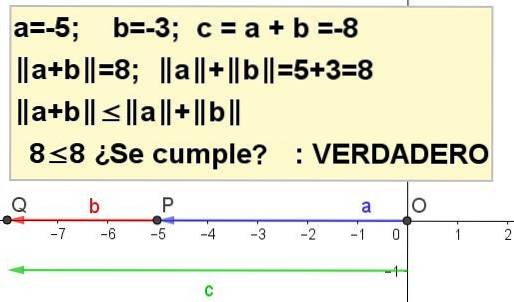
Konstruieren Sie grafisch die dreieckige Ungleichung für a = -5 und b = -3.
| a + b | ≤ | zu | + | b |, Sein c = a + b.
Verweise
- E. Whitesitt. (1980). Boolesche Algebra und ihre Anwendungen. Redaktion Continental C. A..
- Mícheál O 'Searcoid. (2003) Elemente der abstrakten Analyse… Fakultät für Mathematik. Universität Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Mathematik und Ingenieurwissenschaften in der Informatik. Institut für Informatik und Technologie. National Bureau of Standards. Washington, D. C. 20234
- Eric Lehman. Mathematik für die Informatik. Google Inc.
- F Thomson Leighton (1980). Infinitesimalrechnung. Institut für Mathematik und das Labor für Informatik und KI, Massachusetts Institute of Technology.
- Khan Akademie. Dreieck-Ungleichungssatz. Wiederhergestellt von: khanacademy.org
- Wikipedia. Dreieckige Ungleichung. Wiederhergestellt von: es. wikipedia.com

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.