Was sind die Teiler von 30?

Schnell kann es erkannt werden Was sind die Teiler von 30, sowie jede andere Zahl (außer Null), aber die Grundidee besteht darin, zu lernen, wie die Teiler einer Zahl allgemein berechnet werden.

Bei Divisoren ist Vorsicht geboten, da schnell festgestellt werden kann, dass alle Divisoren von 30 1, 2, 3, 5, 6, 10, 15 und 30 sind. Was ist jedoch mit den Negativen dieser Zahlen? Sind sie Teiler oder nicht??

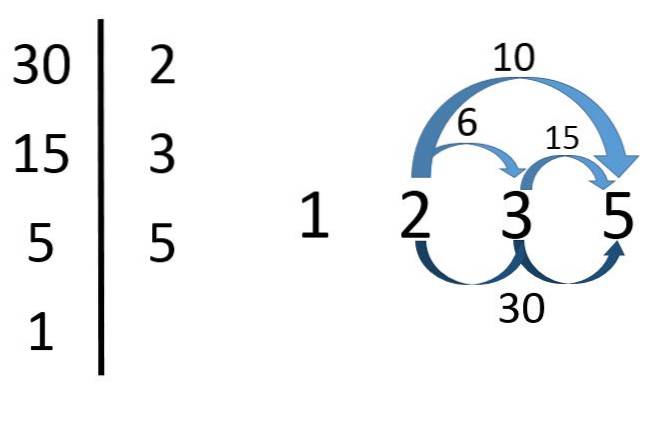
Um die vorherige Frage zu beantworten, muss ein sehr wichtiger Begriff in der Welt der Mathematik verstanden werden: der Divisionsalgorithmus.

Divisionsalgorithmus

Der Divisionsalgorithmus (oder die euklidische Division) sagt Folgendes: Wenn zwei ganze Zahlen "n" und "b" gegeben sind, wobei "b" von Null verschieden ist (b ≠ 0), gibt es nur ganze Zahlen "q" und "r", wie z dass n = bq + r, wobei 0 ≤ r ist < |b|.

Die Zahl "n" wird als Dividende bezeichnet, "b" als Divisor, "q" als Quotient und "r" als Rest oder Rest. Wenn der Rest "r" gleich 0 ist, wird gesagt, dass "b" "n" teilt, und dies wird mit "b | n" bezeichnet..

Der Divisionsalgorithmus ist nicht auf positive Werte beschränkt. Daher kann eine negative Zahl ein Teiler einer anderen Zahl sein.

Warum ist 7.5 kein Teiler von 30??

Unter Verwendung des Divisionsalgorithmus ist ersichtlich, dass 30 = 7,5 × 4 + 0 ist. Der Rest ist gleich Null, aber es kann nicht gesagt werden, dass 7,5 durch 30 dividiert, weil wir, wenn wir über Divisoren sprechen, nur über ganze Zahlen sprechen.

Teiler von 30

Wie im Bild zu sehen ist, müssen zuerst die Primfaktoren gefunden werden, um die Teiler von 30 zu finden.

Also 30 = 2x3x5. Daraus schließen wir, dass 2, 3 und 5 Teiler von 30 sind. Aber auch die Produkte dieser Primfaktoren.

2 × 3 = 6, 2 × 5 = 10, 3 × 5 = 15 und 2x3x5 = 30 sind Teiler von 30. Die 1 ist auch ein Teiler von 30 (obwohl es sich tatsächlich um einen Teiler einer beliebigen Zahl handelt).

Es kann gefolgert werden, dass 1, 2, 3, 5, 6, 10, 15 und 30 Teiler von 30 sind (alle entsprechen dem Teilungsalgorithmus), aber es muss beachtet werden, dass ihre Negative auch Teiler sind.

Daher sind alle Teiler von 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 und 30.

Was oben gelernt wurde, kann auf eine ganze Zahl angewendet werden.

Wenn Sie beispielsweise die Teiler von 92 berechnen möchten, gehen Sie wie zuvor vor. Zersetzt sich als Produkt von Primzahlen.

Teilen Sie 92 durch 2 und erhalten Sie 46; Teilen Sie nun 46 durch 2 und erhalten Sie 23.

Dieses letzte Ergebnis ist eine Primzahl, daher werden neben 1 und derselben 23 keine weiteren Teiler mehr vorhanden sein.

Wir können dann 92 = 2x2x23 schreiben. Nach wie vor wird der Schluss gezogen, dass 1,2,4,46 und 92 Teiler von 92 sind.

Schließlich sind die Negative dieser Zahlen in der vorherigen Liste enthalten, mit der die Liste aller Teiler von 92 -92, -46, -4, -2, -1, 1, 2, 4, 46, 92 ist.

Verweise

1. H. Barrantes, P. Díaz, M. Murillo & A. Soto (1988). Einführung in die Zahlentheorie. San José: EUNED.
2. Bustillo, A. F. (1866). Mathematische Elemente. Imp. Von Santiago Aguado.
3. Guevara, M. H. (s.f.). Zahlentheorie. San José: EUNED.
4. J., A. C. & A., L. T. (1995). Wie man mathematisches logisches Denken entwickelt. Santiago de Chile: Editorial Universitaria.
5. Jiménez, J., Delgado, M. & Gutiérrez, L. (2007). Leitfaden Think II. Threshold Editions.
6. Jiménez, J., Teshiba, M., Teshiba, M., Romo, J., Álvarez, M., Villafania, P., Nesta, B. (2006). Mathematik 1 Arithmetik und Voralgebra. Threshold Editions.
7. Johnsonbaugh, R. (2005). Diskrete Mathematik. Pearson Ausbildung.