
Konstante der Verhältnismäßigkeit was ist das, Berechnung, Übungen
Das Proportionalitätskonstante Es ist ein relationales numerisches Element, das verwendet wird, um das Ähnlichkeitsmuster zwischen zwei Größen zu definieren, die gleichzeitig geändert werden. Es ist sehr üblich, es als lineare Funktion auf generische Weise unter Verwendung des Ausdrucks F (X) = k.X darzustellen. Dies ist jedoch nicht die einzige Darstellung einer möglichen Verhältnismäßigkeit.
Zum Beispiel hat die Beziehung zwischen X und Y in der Funktion Y = 3x eine Proportionalitätskonstante von 3. Es wird beobachtet, dass mit dem Wachstum der unabhängigen Variablen X auch die abhängige Variable Y um das Dreifache ihres vorherigen Wertes wächst.
Die Änderungen, die auf eine Variable angewendet werden, wirken sich unmittelbar auf die andere aus, so dass es einen Wert gibt, der als Proportionalitätskonstante bekannt ist. Dies dient dazu, die unterschiedlichen Größen, die beide Variablen erfassen, in Beziehung zu setzen.
Artikelverzeichnis
- 1 Was ist die Proportionalitäts- und Typkonstante?
- 1.1 Direkte Verhältnismäßigkeit
- 1.2 Inverse oder indirekte Verhältnismäßigkeit
- 2 Wie wird es berechnet??
- 2.1 Entsprechend seiner Grafik
- 2.2 Nach Wertetabelle
- 2.3 Nach analytischem Ausdruck
- 2.4 Durch direkte oder zusammengesetzte Dreierregel
- 3 Geschichte
- 4 Gelöste Übungen
- 4.1 Übung 1
- 4.2 Übung 2
- 5 Referenzen
Was ist die Konstante der Proportionalität und Typen
Entsprechend dem Trend bei der Änderung der Variablen können die Proportionalitäten in zwei Typen eingeteilt werden.
Direkte Verhältnismäßigkeit
Schlägt eine Einwegbeziehung zwischen zwei Größen vor. Wenn die unabhängige Variable ein gewisses Wachstum aufweist, wächst auch die abhängige Variable. In ähnlicher Weise führt jede Abnahme der unabhängigen Variablen zu einer Abnahme der Größe von Y..
Zum Beispiel die in der Einleitung verwendete lineare Funktion; Y = 3X entspricht einer direkten Proportionalitätsbeziehung. Dies liegt daran, dass die Erhöhung der unabhängigen Variablen X eine dreifache Erhöhung des vorherigen Werts der abhängigen Variablen Y bewirkt.
In ähnlicher Weise verringert sich die abhängige Variable um das Dreifache ihres Wertes, wenn die Größe von X abnimmt.
Der Wert der Proportionalitätskonstante "K" in einer direkten Beziehung ist definiert als K = Y / X..
Inverse oder indirekte Verhältnismäßigkeit
Bei dieser Art von Funktionen wird die Beziehung zwischen den Variablen antonym dargestellt, wobei das Wachstum oder die Abnahme der unabhängigen Variablen jeweils der Abnahme oder dem Wachstum der abhängigen Variablen entspricht..
Zum Beispiel ist die Funktion F (x) = k / x eine umgekehrte oder indirekte Beziehung. Da der Wert der unabhängigen Variablen zu steigen beginnt, wird der Wert von k durch eine zunehmende Zahl geteilt, wodurch die abhängige Variable entsprechend dem Anteil an Wert verliert.
Abhängig von dem von K angenommenen Wert kann der Trend der inversen Proportionalfunktion definiert werden. Wenn k> 0 ist, nimmt die Funktion bei allen reellen Zahlen ab. Und sein Graph wird im 1. und 3. Quadranten sein.
Wenn im Gegensatz dazu der Wert von K negativ oder kleiner als Null ist, nimmt die Funktion zu und ihr Graph befindet sich im 2. und 4. Quadranten.
Wie wird es berechnet??
Es gibt verschiedene Kontexte, in denen die Definition der Proportionalitätskonstante erforderlich sein kann. In den verschiedenen Fällen werden verschiedene Daten über das Problem gezeigt, wobei die Untersuchung dieser schließlich den Wert von K ergibt.
Generisch kann das oben Genannte zusammengefasst werden. Die Werte von K entsprechen zwei Ausdrücken in Abhängigkeit von der Art der vorhandenen Proportionalität:
- Direkt: K = Y / X.
- Invers oder indirekt: K = Y.X.
Nach seiner Grafik
Manchmal ist der Graph einer Funktion nur teilweise oder vollständig bekannt. In diesen Fällen muss durch grafische Analyse die Art der Verhältnismäßigkeit bestimmt werden. Dann muss eine Koordinate definiert werden, mit der die Werte von X und Y überprüft werden können, um sie auf die entsprechende Formel von K anzuwenden.
Die Diagramme, die sich auf direkte Proportionalitäten beziehen, sind linear. Andererseits haben die Graphen der inversen Proportionalfunktionen normalerweise die Form von Hyperbeln.
Nach Wertetabelle
In einigen Fällen gibt es eine Wertetabelle mit den Werten, die jeder Iteration der unabhängigen Variablen entsprechen. Normalerweise impliziert dies die Realisierung des Graphen zusätzlich zur Definition des Wertes von K..
Nach analytischem Ausdruck
Gibt den Ausdruck zurück, der die Funktion analytisch definiert. Der Wert von K kann direkt gelöst oder auch aus dem Ausdruck selbst abgeleitet werden.
Durch direkte oder zusammengesetzte Dreierregel
In anderen Übungsmodellen werden bestimmte Daten dargestellt, die sich auf die Beziehung zwischen den Werten beziehen. Dies macht es erforderlich, die direkte oder zusammengesetzte Dreierregel anzuwenden, um andere notwendige Daten in der Übung zu definieren..
Geschichte
Das Konzept der Verhältnismäßigkeit gab es schon immer. Nicht nur im Kopf und in der Arbeit der großen Mathematiker, sondern auch im täglichen Leben der Bevölkerung aufgrund seiner Praktikabilität und Anwendbarkeit.
Es ist sehr häufig, Situationen zu finden, die einen Verhältnismäßigkeitsansatz erfordern. Diese werden jeweils dort dargestellt, wo Variablen und Phänomene mit bestimmten Beziehungen verglichen werden müssen.
Durch eine Zeitleiste können wir die historischen Momente charakterisieren, in denen mathematische Fortschritte in Bezug auf die Verhältnismäßigkeit angewendet wurden..
- 2. Jahrhundert v Das Fraktions- und Proportionsspeichersystem wird in Griechenland eingeführt.
- 5. Jahrhundert v Das Verhältnis, das die Seite und die Diagonale eines Quadrats in Beziehung setzt, wird auch in Griechenland entdeckt.
- 600 v Thales von Milet stellt seinen Satz über die Verhältnismäßigkeit vor.
- Jahr 900. Das zuvor von Indien verwendete Dezimalsystem wird in Verhältnissen und Proportionen erweitert. Beitrag der Araber.
- XVII Jahrhundert. Beiträge zu den Anteilen kommen in Eulers Berechnung an.
- XIX Jahrhundert. Gauß trägt das Konzept der komplexen Anzahl und Proportionen bei.
- 20. Jahrhundert. Die Proportionalität als Funktionsmodell wird von Azcarate und Deulofeo definiert.

Gelöste Übungen
Übung 1
Es ist erforderlich, den Wert der Variablen x, y, z und g zu berechnen. Kenntnis der folgenden proportionalen Beziehungen:
3x + 2y - 6z + 8g = 1925
x / 3 = y / 8 = z / 3 = g / 5
Wir fahren fort, die relativen Werte der Proportionalitätskonstante zu definieren. Diese können aus der zweiten Beziehung erhalten werden, wobei der Wert, der jede Variable teilt, eine Beziehung oder ein Verhältnis angibt, das sich auf K bezieht.
X = 3k y = 2k z = 3k g = 5k
Die Werte werden im ersten Ausdruck ersetzt, wobei das neue System in einer einzelnen Variablen k ausgewertet wird.
3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925
9k + 4k -18k + 40k = 1925
35k = 1925
K = 1925/35 = 55
Unter Verwendung dieses Wertes der Proportionalitätskonstante können wir die Zahl finden, die jede der Variablen definiert.
x = 3 (55) = 165 y = 2 (55) = 110
z = 3 (55) = 165 g = 5 (55) = 275
Übung 2
Berechnen Sie die Proportionalitätskonstante und den Ausdruck, der die Funktion definiert, anhand ihres Diagramms.
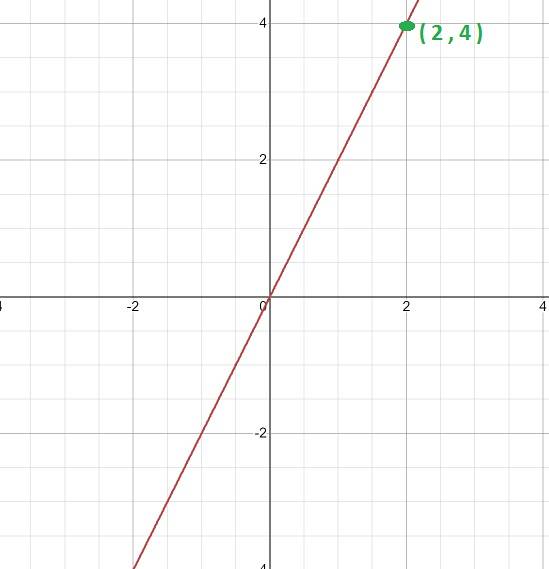
Zunächst wird der Graph analysiert, wobei sein linearer Charakter offensichtlich ist. Dies zeigt an, dass es sich um eine Funktion mit direkter Proportionalität handelt und dass der Wert von K durch den Ausdruck k = y / x erhalten wird
Dann wird aus dem Diagramm ein bestimmbarer Punkt ausgewählt, dh einer, an dem die Koordinaten, aus denen er besteht, genau sichtbar sind..
Für diesen Fall wird der Punkt (2, 4) genommen. Von wo aus können wir die folgende Beziehung herstellen.
K = 4/2 = 2
Der Ausdruck wird also durch die Funktion y = kx definiert, die in diesem Fall sein wird
F (x) = 2x
Verweise
- Mathematik für Elektrizität und Elektronik. Dr. Arthur Kramer. Cengage Learning, 27. Juli 2012
- Vision 2020: Die strategische Rolle der operativen Forschung. N. Ravichandran. Allied Publishers, 11. September. 2005
- Grammatik- und Rechenkenntnisse des Verwaltungsassistenten des Staates. E-Book. MAD-Eduforma
- Verstärkung der Mathematik zur Unterstützung und Diversifizierung des Lehrplans: zur Unterstützung und Diversifizierung des Lehrplans. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29. August. 2003
- Logistik und kaufmännisches Management. Maria José Escudero Serrano. Ediciones Paraninfo, S. A., 1 sept. 2013



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.