
Kompressibilität von Feststoffen, Flüssigkeiten, Gasen, Beispiele
Das Kompressibilität eines Stoffes oder Materials ist die Volumenänderung, die es erfährt, wenn es einer Druckänderung ausgesetzt wird. Im Allgemeinen nimmt das Volumen ab, wenn Druck auf ein System oder Objekt ausgeübt wird. Manchmal passiert jedoch das Gegenteil: Eine Druckänderung kann zu einer Explosion führen, bei der das System an Volumen zunimmt oder wenn eine Phasenänderung stattfindet..
Bei einigen chemischen Reaktionen und auch bei Gasen kann dies passieren, da mit zunehmender Häufigkeit von Kollisionen die Abstoßungskräfte auftreten..

Berücksichtigen Sie bei der Vorstellung, wie einfach oder schwierig es sein kann, ein Objekt zu komprimieren, die drei Zustände, in denen sich die Materie normalerweise befindet: fest, flüssig und gasförmig. In jedem von ihnen halten die Moleküle bestimmte Abstände voneinander. Je stärker die Bindungen sind, die die Moleküle der Substanz verbinden, aus denen das Objekt besteht, und je näher sie sind, desto schwieriger wird es, eine Verformung zu verursachen.
Ein Feststoff hat seine Moleküle sehr nahe beieinander, und wenn versucht wird, sie näher zusammenzubringen, treten abstoßende Kräfte auf, die die Aufgabe schwierig machen. Daher wird gesagt, dass Feststoffe nicht sehr komprimierbar sind. In den Flüssigkeitsmolekülen ist mehr Platz vorhanden, so dass ihre Kompressibilität größer ist, aber dennoch erfordert die Volumenänderung normalerweise große Kräfte.
Feststoffe und Flüssigkeiten sind also kaum komprimierbar. Es würde eine sehr große Druckschwankung erfordern, um eine nennenswerte Volumenänderung unter sogenannten normalen Druck- und Temperaturbedingungen zu erreichen. Andererseits können Gase, da ihre Moleküle weit voneinander entfernt sind, leicht komprimiert und dekomprimiert werden.
Artikelverzeichnis
- 1 Kompressibilität von Feststoffen
- 1.1 -Komprimierbarkeit eines Materials
- 2 Gelöste Übungsbeispiele
- 2.1 - Gelöste Übung 1
- 2.2 - Gelöste Übung 2
- 2.3 - Gelöste Übung 3
- 3 Kompressibilität in Gasen
- 3.1 - Gelöste Übung 5
- 4 Referenzen
Feste Kompressibilität
Wenn ein Objekt beispielsweise in eine Flüssigkeit eingetaucht ist, übt es Druck in alle Richtungen auf das Objekt aus. Auf diese Weise können wir davon ausgehen, dass das Volumen des Objekts abnimmt, obwohl dies in den meisten Fällen nicht spürbar ist..
Die Situation ist in der folgenden Abbildung dargestellt:
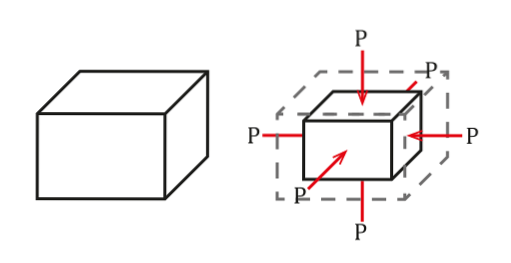
Der Druck ist definiert als Kraft pro Flächeneinheit, die eine Volumenänderung ΔV proportional zum Anfangsvolumen des Objekts V verursachtoder. Diese Volumenänderung hängt von seinen Eigenschaften ab..
Das Hookesche Gesetz besagt, dass die Verformung eines Objekts proportional zu der auf es ausgeübten Spannung ist:
Stress ∝ Dehnung
Die volumetrische Verformung eines Körpers wird durch B, die erforderliche Proportionalitätskonstante, quantifiziert, die als bezeichnet wird Volumenmodul des Materials::
B = -Stress / Dehnung
B = -ΔP / (ΔV / V.oder)
Als ΔV / V.oder ist eine dimensionslose Größe, da es sich um den Quotienten zwischen zwei Volumina handelt, hat das Volumenmodul die gleichen Druckeinheiten, die im internationalen System Pascal (Pa) sind..
Das negative Vorzeichen zeigt die erwartete Volumenverringerung an, wenn das Objekt ausreichend komprimiert ist, dh der Druck steigt.
-Kompressibilität eines Materials
Der inverse oder reziproke Wert des Volumenmoduls ist bekannt als Kompressibilität und wird durch den Buchstaben bezeichnet k. Deshalb:

Hier k ist das Negativ der fraktionierten Volumenänderung pro Druckanstieg. Seine Einheiten im internationalen System sind die Umkehrungen von Pa, dh mzwei / N..
Die Gleichung für B oder für k, wenn Sie dies bevorzugen, gilt sowohl für Feststoffe als auch für Flüssigkeiten. Das Konzept des Volumenmoduls wird selten auf Gase angewendet. Ein einfaches Modell zur Quantifizierung der Volumenverringerung, die ein echtes Gas erfahren kann, wird nachstehend erläutert..
Die Schallgeschwindigkeit und der Kompressibilitätsmodul
Eine interessante Anwendung ist die Schallgeschwindigkeit in einem Medium, die von seinem Kompressibilitätsmodul abhängt:

Gelöste Übungsbeispiele
-Gelöste Übung 1
Eine massive Messingkugel mit einem Volumen von 0,8 m3 Es wird bis zu einer Tiefe in den Ozean fallen gelassen, in der der hydrostatische Druck 20 M Pa höher ist als an der Oberfläche. Wie wird sich das Volumen der Kugel ändern? Es ist bekannt, dass der Kompressibilitätsmodul von Messing ist B. = 35.000 MPa,
Lösung
1 M Pa = 1 Megapascal = 1. 10 6 Pa
Die Druckänderung in Bezug auf die Oberfläche beträgt DP = 20 × 10 6 Pa. Unter Anwendung der für B angegebenen Gleichung haben wir:
B = -ΔP / (ΔV / V.oder)
Deshalb:

ΔV = -5,71,10 -4 x 0,8 m3 = -4,57 x 10-4 m3
Die Volumendifferenz kann ein negatives Vorzeichen haben, wenn das Endvolumen kleiner als das Anfangsvolumen ist. Daher stimmt dieses Ergebnis mit allen bisher getroffenen Annahmen überein.
Der sehr hohe Kompressibilitätsmodul zeigt an, dass eine große Druckänderung erforderlich ist, damit das Objekt eine merkliche Volumenverringerung erfährt..
-Übung gelöst 2
Indem Sie Ihr Ohr gegen die Eisenbahnschienen legen, können Sie erkennen, wann sich eines dieser Fahrzeuge in der Ferne nähert. Wie lange dauert der Klang auf einer Stahlschiene, wenn der Zug 1 km entfernt ist??
Daten
Stahldichte = 7,8 x 10 3 kg / m3
Stahlkompressibilitätsmodul = 2,0 x 10 elf Pa.
Lösung

Der oben berechnete Kompressibilitätsmodul B gilt auch für Flüssigkeiten, obwohl im Allgemeinen ein großer Aufwand erforderlich ist, um eine merkliche Volumenverringerung zu erzielen. Flüssigkeiten können sich jedoch ausdehnen oder zusammenziehen, wenn sie sich erwärmen oder abkühlen, und ebenso, wenn sie drucklos oder unter Druck stehen..
Für Wasser unter Standardbedingungen von Druck und Temperatur (0 ° C und ein Atmosphärendruck ungefähr oder 100 kPa) beträgt der Volumenmodul 2100 MPa. Das ist ungefähr das 21.000-fache des atmosphärischen Drucks.
Aus diesem Grund werden Flüssigkeiten in den meisten Anwendungen normalerweise als inkompressibel angesehen. Dies kann sofort mit numerischer Anwendung überprüft werden.
-Übung gelöst 3
Finden Sie die fraktionierte Abnahme des Wasservolumens, wenn es einem Druck von 15 MPa ausgesetzt wird.
Lösung

Kompressibilität in Gasen
Gase funktionieren, wie oben erläutert, etwas anders.
Um zu wissen, welches Volumen sie haben n Mol eines gegebenen Gases, wenn es auf einem Druck gehalten wird P. und bei einer Temperatur T., Die Zustandsgleichung wird verwendet. In der Zustandsgleichung für ein ideales Gas, in der intermolekulare Kräfte nicht berücksichtigt werden, heißt es im einfachsten Modell:
P.V.Ideal = n. R. T.
Wobei R die ideale Gaskonstante ist.
Änderungen des Gasvolumens können bei konstantem Druck oder konstanter Temperatur durchgeführt werden. Zum Beispiel durch Konstanthalten der Temperatur wird die isotherme Kompressibilität ΚT. es ist:

Anstelle des Symbols "Delta", das zuvor bei der Definition des Konzepts für Feststoffe verwendet wurde, wird es für ein Gas mit einer Ableitung, in diesem Fall einer partiellen Ableitung in Bezug auf P, beschrieben, wobei T konstant gehalten wird.
Deshalb B.T. Der isotherme Kompressibilitätsmodul beträgt:

Wichtig ist auch der adiabatische Kompressibilitätsmodul B.adiabatisch, für die es keinen ein- oder ausgehenden Wärmestrom gibt.
B.adiabatisch = γp
Wobei γ der adiabatische Koeffizient ist. Mit diesem Koeffizienten kann die Schallgeschwindigkeit in Luft berechnet werden:

Wenden Sie die obige Gleichung an, um die Schallgeschwindigkeit in Luft zu ermitteln.
Daten
Der adiabatische Kompressibilitätsmodul von Luft beträgt 1,42 × 105 Pa
Die Luftdichte beträgt 1.225 kg / m3 (bei atmosphärischem Druck und 15 ºC)
Lösung

Anstatt mit dem Kompressibilitätsmodul zu arbeiten, wird als Einheitsvolumenänderung pro Druckänderung die Kompressibilitätsfaktor eines echten Gases, ein anderes, aber anschauliches Konzept, wie echtes Gas mit idealem Gas verglichen wird:
P. P. V.Real = Z. R. T.
Wobei Z der Kompressibilitätskoeffizient des Gases ist, der von den Bedingungen abhängt, unter denen es gefunden wird, im Allgemeinen eine Funktion sowohl des Drucks P als auch der Temperatur T ist und ausgedrückt werden kann als:
Z = f (P, T)
Im Falle eines idealen Gases ist Z = 1. Bei realen Gasen steigt der Z-Wert fast immer mit dem Druck an und nimmt mit der Temperatur ab.
Mit zunehmendem Druck kollidieren die gasförmigen Moleküle häufiger und die Abstoßungskräfte zwischen ihnen nehmen zu. Dies kann zu einer Volumenvergrößerung im realen Gas führen, wobei Z> 1 ist.
Im Gegensatz dazu können sich die Moleküle bei niedrigeren Drücken frei bewegen und es überwiegen Anziehungskräfte. In einem solchen Fall ist Z. < 1.
Für den einfachen Fall von 1 Mol Gas n = 1 erhalten wir, wenn die gleichen Druck- und Temperaturbedingungen beibehalten werden, indem wir die vorherigen Gleichungen Term für Term teilen:

V.Real = Z V.Ideal
-Übung gelöst 5
Es gibt ein echtes Gas bei 250 ºK und 15 atm Druck, dessen Molvolumen 12% unter dem nach der idealen Gaszustandsgleichung berechneten liegt. Wenn Druck und Temperatur konstant gehalten werden, finden Sie:
a) Der Kompressibilitätsfaktor.
b) Das Molvolumen des realen Gases.
c) Welche Art von Kräften überwiegt: attraktiv oder abstoßend?
Lösung
a) Wenn das reale Volumen 12% unter dem Ideal liegt, bedeutet dies:
V.Real = 0,88 V.Ideal
Daher beträgt der Kompressibilitätsfaktor für 1 Mol Gas:
Z = 0,88
b) Auswahl der idealen Gaskonstante mit den entsprechenden Einheiten für die gelieferten Daten:
R = 0,082 l / mol
Das Molvolumen wird durch Lösen und Ersetzen von Werten berechnet:
c) Es überwiegen die Anziehungskräfte, da Z kleiner als 1 ist.
Verweise
- Atkins, P. 2008. Physikalische Chemie. Editorial Médica Panamericana. 10 - 15.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6th. Ed Prentice Hall. 242 - 243 und 314-15
- Mott, R. 2006. Fluid Mechanics. Pearson Education 13-14.
- Rex, A. 2011. Grundlagen der Physik. Pearson Ausbildung. 242-243.
- Tipler, P. (2006) Physik für Wissenschaft und Technologie. 5. Aufl. Band 1. Editorial Reverté. 542.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.