Das Bestimmtheitsmaß ist eine Zahl zwischen 0 und 1, die den Bruchteil der Punkte (X, Y) darstellt, die der Regressionsanpassungslinie eines Datensatzes mit zwei Variablen folgen.
Es ist auch bekannt als Güte der Anpassung und wird mit R bezeichnetzwei. Um es zu berechnen, wird der Quotient zwischen der Varianz der durch das Regressionsmodell geschätzten Daten Ŷi und der Varianz der Daten Yi, die jedem Xi der Daten entsprechen, genommen.
R.zwei = Sŷ / Sy
Wenn sich 100% der Daten auf der Linie der Regressionsfunktion befinden, beträgt der Bestimmungskoeffizient 1.
Im Gegenteil, wenn für einen Datensatz und eine bestimmte Anpassungsfunktion der Koeffizient R.zwei stellt sich heraus, gleich 0,5 zu sein, dann kann gesagt werden, dass die Passform zu 50% zufriedenstellend oder gut ist.
In ähnlicher Weise, wenn das Regressionsmodell Werte von R zurückgibtzwei niedriger als 0,5 zeigt dies an, dass sich die gewählte Anpassungsfunktion nicht zufriedenstellend an die Daten anpasst, daher ist es notwendig, nach einer anderen Anpassungsfunktion zu suchen.
Und wenn die Kovarianz oder der Korrelationskoeffizient tendiert gegen Null, dann sind die Variablen X und Y in den Daten nicht miteinander verbunden, und daher R.zwei wird auch gegen Null tendieren.
Artikelverzeichnis
Im vorherigen Abschnitt wurde gesagt, dass der Bestimmungskoeffizient berechnet wird, indem der Quotient zwischen den Varianzen ermittelt wird:
-Geschätzt durch die Regressionsfunktion der Variablen Y.
-Die der Variablen Yi, die jeder der Variablen Xi der N Datenpaare entspricht.
Mathematisch ausgedrückt sieht es so aus:
R.zwei = Sŷ / Sy
Aus dieser Formel folgt, dass R.zwei stellt den Anteil der Varianz dar, der durch das Regressionsmodell erklärt wird. Alternativ kann R berechnet werdenzwei unter Verwendung der folgenden Formel, die der vorherigen völlig gleichwertig ist:
R.zwei = 1 - (S & epsi; / Sy)
Wobei Sε die Varianz der Residuen εi = Ŷi - Yi darstellt, während Sy die Varianz des Satzes von Yi-Werten der Daten ist. Um Ŷi zu bestimmen, wird die Regressionsfunktion angewendet, was bedeutet, dass Ŷi = f (Xi).
Die Varianz des Datensatzes Yi mit i von 1 bis N wird wie folgt berechnet:
Sy = [Σ (Yi -
Und dann verfahren Sie auf ähnliche Weise für Sŷ oder für Sε.
Um das Detail zu zeigen, wie die Berechnung der Bestimmtheitsmaß Wir werden den folgenden Satz von vier Datenpaaren nehmen:
(X, Y): (1, 1); (2. 3); (3, 6) und (4, 7).
Für diesen Datensatz wird eine lineare Regressionsanpassung vorgeschlagen, die mit der Methode der kleinsten Quadrate erhalten wird:
f (x) = 2,1 x - 1
Durch Anwenden dieser Einstellfunktion werden die Drehmomente erhalten:
(X, Ŷ): (1, 1.1); (2, 3,2); (3, 5.3) und (4, 7.4).
Dann berechnen wir das arithmetische Mittel für X und Y:
Varianz Sy
Sy = [(1 - 4,25)zwei + (3 - 4,25)zwei + (6 - 4,25)zwei +….…. (7 - 4.25)zwei] / (4-1) =
= [(-3,25)zwei+ (-1,25)zwei + (1,75)zwei + (2,75)zwei) / (3)] = 7,583
Varianz Sŷ
S = [(1,1 - 4,25)zwei + (3,2 - 4,25)zwei + (5,3 - 4,25)zwei +….…. (7.4 - 4.25)zwei] / (4-1) =
= [(-3,25)zwei + (-1,25)zwei + (1,75)zwei + (2,75)zwei) / (3)] = 7,35
Bestimmungskoeffizient R.zwei
R.zwei = Sŷ / Sy = 7,35 / 7,58 = 0,97
Der Bestimmungskoeffizient für den im vorherigen Segment betrachteten veranschaulichenden Fall betrug 0,98. Mit anderen Worten, die lineare Anpassung durch die Funktion:
f (x) = 2,1x - 1
Es ist zu 98% zuverlässig bei der Erklärung der Daten, mit denen es unter Verwendung der Methode der kleinsten Quadrate erhalten wurde..
Neben dem Bestimmungskoeffizienten gibt es die linearer Korrelationskoeffizient oder auch als Pearson-Koeffizient bekannt. Dieser Koeffizient wird bezeichnet als r, wird durch die folgende Beziehung berechnet:
r = Sxy / (Sx Sy)
Hier repräsentiert der Zähler die Kovarianz zwischen den Variablen X und Y, während der Nenner das Produkt der Standardabweichung für die Variable X und der Standardabweichung für die Variable Y ist.
Der Pearson-Koeffizient kann Werte zwischen -1 und +1 annehmen. Wenn dieser Koeffizient gegen +1 tendiert, gibt es eine direkte lineare Korrelation zwischen X und Y. Wenn er stattdessen gegen -1 tendiert, gibt es eine lineare Korrelation, aber wenn X zunimmt, nimmt Y ab. Schließlich ist es nahe 0, es gibt keine Korrelation zwischen den beiden Variablen.
Es ist zu beachten, dass der Bestimmungskoeffizient nur dann mit dem Quadrat des Pearson-Koeffizienten übereinstimmt, wenn der erste auf der Grundlage einer linearen Anpassung berechnet wurde. Diese Gleichheit gilt jedoch nicht für andere nichtlineare Anpassungen..
Eine Gruppe von Schülern machte sich daran, ein empirisches Gesetz für die Dauer eines Pendels als Funktion seiner Länge zu bestimmen. Um dieses Ziel zu erreichen, führen sie eine Reihe von Messungen durch, bei denen sie die Zeit einer Pendelschwingung für verschiedene Längen messen und dabei folgende Werte erhalten:
| Länge (m) | Zeitraum (e) |
|---|---|
| 0,1 | 0,6 |
| 0,4 | 1.31 |
| 0,7 | 1,78 |
| 1 | 1,93 |
| 1.3 | 2.19 |
| 1.6 | 2.66 |
| 1.9 | 2,77 |
| 3 | 3.62 |
Es wird angefordert, ein Streudiagramm der Daten zu erstellen und eine lineare Anpassung durch Regression durchzuführen. Zeigen Sie auch die Regressionsgleichung und ihren Bestimmungskoeffizienten.
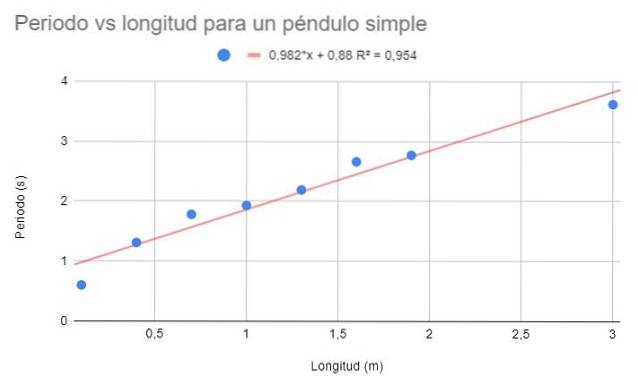
Es kann ein ziemlich hoher Bestimmungskoeffizient beobachtet werden (95%), so dass angenommen werden kann, dass die lineare Anpassung optimal ist. Wenn die Punkte jedoch zusammen betrachtet werden, scheint es, dass sie dazu neigen, sich nach unten zu krümmen. Dieses Detail wird im linearen Modell nicht berücksichtigt.
Erstellen Sie für dieselben Daten in Beispiel 1 ein Streudiagramm der Daten. In diesem Fall wird im Gegensatz zu Beispiel 1 eine Regressionsanpassung unter Verwendung einer potenziellen Funktion angefordert.
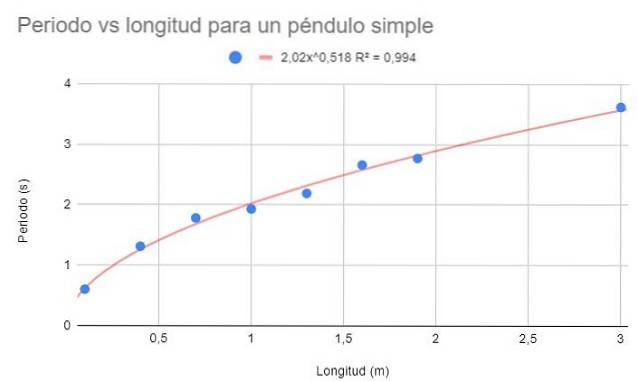
Zeigen Sie auch die Anpassungsfunktion und ihren Bestimmungskoeffizienten R.zwei.
Die potentielle Funktion hat die Form f (x) = AxB., wobei A und B Konstanten sind, die durch die Methode der kleinsten Quadrate bestimmt werden.
Die vorige Abbildung zeigt die Potentialfunktion und ihre Parameter sowie den Bestimmungskoeffizienten mit einem sehr hohen Wert von 99%. Beachten Sie, dass die Daten der Krümmung der Trendlinie folgen.
Führen Sie unter Verwendung der gleichen Daten aus Beispiel 1 und Beispiel 2 eine Polynomanpassung zweiten Grades durch. Grafik, Anpassungspolynom und Bestimmungskoeffizient R anzeigenzwei Korrespondent.
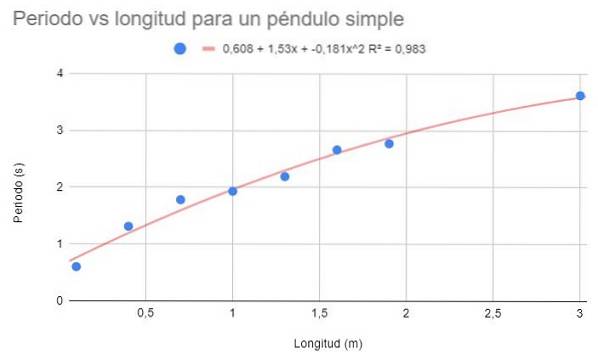
Mit der Polynomanpassung zweiten Grades können Sie eine Trendlinie sehen, die gut zur Krümmung der Daten passt. Der Bestimmungskoeffizient liegt auch über der linearen Anpassung und unter der potenziellen Anpassung..
Von den drei gezeigten Anpassungen ist diejenige mit dem höchsten Bestimmungskoeffizienten die potenzielle Anpassung (Beispiel 2)..
Die potentielle Anpassung stimmt mit der physikalischen Theorie des Pendels überein, die bekanntlich feststellt, dass die Periode eines Pendels proportional zur Quadratwurzel seiner Länge ist, wobei die Proportionalitätskonstante 2π / √g ist, wobei g die Beschleunigung von ist Schwere.
Diese Art der Potentialanpassung hat nicht nur den höchsten Bestimmungskoeffizienten, sondern der Exponent und die Proportionalitätskonstante stimmen mit dem physikalischen Modell überein..
-Die Regressionsanpassung bestimmt die Parameter der Funktion, die die Daten unter Verwendung der Methode der kleinsten Quadrate erklären soll. Diese Methode besteht darin, die Summe der quadratischen Differenz zwischen dem Y-Wert der Anpassung und dem Yi-Wert der Daten für die Xi-Werte der Daten zu minimieren. Dies bestimmt die Parameter der Einstellfunktion.
-Wie wir gesehen haben, ist die Linie die häufigste Anpassungsfunktion, aber nicht die einzige, da die Anpassungen auch polynomisch, potentiell, exponentiell, logarithmisch und andere sein können..
-In jedem Fall hängt der Bestimmungskoeffizient von den Daten und der Art der Anpassung ab und ist ein Hinweis auf die Güte der angewendeten Anpassung..
-Schließlich gibt der Bestimmungskoeffizient den Prozentsatz der Gesamtvariabilität zwischen dem Y-Wert der Daten in Bezug auf den Ŷ-Wert der Anpassung für das gegebene X an.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.