Elastische Schocks in einer Dimension, Sonderfälle, Übungen

Das elastische Stöße oder elastische Kollisionen bestehen aus kurzen, aber intensiven Wechselwirkungen zwischen Objekten, bei denen sowohl der Impuls als auch die kinetische Energie erhalten bleiben. Abstürze sind in der Natur sehr häufig: Von subatomaren Partikeln über Galaxien bis hin zu Billardkugeln und Autoscootern in Vergnügungsparks sind alles Objekte, die kollidieren können.

Während einer Kollision oder Kollision sind die Wechselwirkungskräfte zwischen Objekten sehr stark, viel stärker als diejenigen, die extern wirken können. Auf diese Weise kann festgestellt werden, dass die Partikel während der Kollision ein isoliertes System bilden.

In diesem Fall ist es wahr, dass:

P._oder = P._F.

Das Ausmaß der Bewegung P._oder vor der Kollision ist das gleiche wie nach der Kollision. Dies gilt für jede Art von Kollision, sowohl elastisch als auch unelastisch..

Beachten Sie nun Folgendes: Während einer Kollision erfahren Objekte eine gewisse Verformung. Wenn der Stoß elastisch ist, nehmen Objekte schnell ihre ursprüngliche Form wieder an.

Artikelverzeichnis

• 1 Erhaltung der kinetischen Energie
• 2 Elastische Stöße in einer Dimension
  • 2.1 -Formeln für elastische Kollisionen
• 3 Sonderfälle bei elastischen Kollisionen
  • 3.1 Zwei identische Massen
  • 3.2 Zwei identische Massen, von denen eine anfänglich in Ruhe war
  • 3.3 Zwei verschiedene Massen, eine davon zunächst in Ruhe
• 4 Restitutionskoeffizient oder Huygens-Newton-Regel
• 5 Übungen gelöst
  • 5.1 - Gelöste Übung 1
  • 5.2 - Gelöste Übung 2
  • 5.3 - Gelöste Übung 3
  • 5.4 - Gelöste Übung 4
• 6 Referenzen

Erhaltung der kinetischen Energie

Normalerweise wird während eines Unfalls ein Teil der Energie von Objekten für Wärme, Verformung, Schall und manchmal sogar für die Erzeugung von Licht aufgewendet. Die kinetische Energie des Systems nach der Kollision ist also geringer als die ursprüngliche kinetische Energie.

Wenn die kinetische Energie K erhalten bleibt, dann:

K._oder = K._F.

Dies bedeutet, dass die während der Kollision wirkenden Kräfte konservativ sind. Während der Kollision wird die kinetische Energie kurz in potentielle Energie und dann zurück in kinetische Energie umgewandelt. Die jeweiligen kinetischen Energien variieren, aber die Summe bleibt konstant.

Perfekt elastische Kollisionen sind selten, obwohl Billardkugeln eine ziemlich gute Annäherung sind, ebenso wie Kollisionen, die zwischen idealen Gasmolekülen auftreten..

Elastische Stöße in einer Dimension

Lassen Sie uns eine Kollision zweier Partikel in einer einzigen Dimension untersuchen. Das heißt, die wechselwirkenden Teilchen bewegen sich beispielsweise entlang der x-Achse. Angenommen, sie haben Massen m₁ Y. m_zwei. Die Anfangsgeschwindigkeiten von jedem sind oder₁ Y. oder_zwei beziehungsweise. Endgeschwindigkeiten sind v₁ Y. v_zwei.

Wir können auf die Vektornotation verzichten, da die Bewegung entlang der x-Achse ausgeführt wird. Die Zeichen (-) und (+) geben jedoch die Bewegungsrichtung an. Links ist konventionell negativ und rechts positiv.

-Formeln für elastische Kollisionen

Für die Menge an Bewegung

m₁oder₁ + m_zweioder_zwei = m₁v₁ + m_zweiv_zwei

Für kinetische Energie

½ m₁oder^zwei₁ + ½ m_zweioder^zwei_zwei = ½ m₁v^zwei₁ +  ½ m_zweiv^zwei_zwei

Vorausgesetzt, die Massen und Anfangsgeschwindigkeiten sind bekannt, können die Gleichungen neu gruppiert werden, um die Endgeschwindigkeiten zu finden.

Das Problem ist, dass im Prinzip eine etwas langwierige Algebra durchgeführt werden muss, da die Gleichungen für die kinetische Energie die Quadrate der Geschwindigkeiten enthalten, was die Berechnung etwas umständlich macht. Das Ideal wäre, Ausdrücke zu finden, die sie nicht enthalten.

Das erste ist, auf den Faktor ½ zu verzichten und beide Gleichungen so neu anzuordnen, dass ein negatives Vorzeichen erscheint und die Massen berücksichtigt werden können:

m₁oder₁ - m₁v₁ = M._zweiv_zwei - m_zweioder_zwei

m₁oder^zwei₁ - m₁v^zwei₁  = + M._zweiv^zwei_zwei - m_zweioder^zwei_zwei

Auf diese Weise ausgedrückt werden:

m₁(oder₁ - v₁ ) = m_zwei(v_zwei - oder_zwei)

m₁(oder^zwei₁ - v^zwei₁ ) = m_zwei (v^zwei_zwei - oder^zwei_zwei)

Vereinfachung zur Beseitigung der Quadrate der Geschwindigkeiten

Jetzt müssen wir die bemerkenswerte Summe des Produkts durch seine Differenz in der zweiten Gleichung verwenden, mit der wir einen Ausdruck erhalten, der die Quadrate nicht enthält, wie ursprünglich gewünscht:

m₁(oder₁ - v₁ ) = m_zwei(v_zwei - oder_zwei)

m₁(oder₁ - v₁ ) (oder₁ + v₁ ) = m_zwei (v_zwei - oder_zwei) (v_zwei + oder_zwei)

Der nächste Schritt besteht darin, die erste Gleichung durch die zweite zu ersetzen:

m_zwei(v_zwei - oder_zwei) (oder₁ + v₁ ) = m_zwei (v_zwei - oder_zwei) (v_zwei + oder_zwei)

Und wenn der Begriff wiederholt wird m_zwei(v_zwei - oder_zwei) Auf beiden Seiten der Gleichstellung wird dieser Begriff annulliert und sieht folgendermaßen aus:

(oder₁ + v₁) = (v_zwei + oder_zwei)

Oder noch besser:

oder₁ - oder_zwei= v_zwei -  v₁

Endgeschwindigkeiten v₁ und V._zwei der Partikel

Jetzt haben Sie zwei lineare Gleichungen, mit denen Sie leichter arbeiten können. Wir werden sie wieder untereinander legen:

m₁oder₁ + m_zweioder_zwei = m₁v₁ + m_zweiv_zwei

oder₁ - oder_zwei= v_zwei -  v₁

Multiplizieren Sie die zweite Gleichung mit m₁ und Hinzufügen von Begriff zu Begriff ist:

m₁oder₁ + m_zweioder_zwei = m₁v₁ + m_zweiv_zwei

m₁oder₁ - m₁oder_zwei= m₁v_zwei - m₁ v₁

-

2 m₁oder₁ + (m_zwei - m₁) oder_zwei = (m_zwei + m₁) v_zwei

Und es ist bereits möglich zu löschen v_zwei. Beispielsweise:

Sonderfälle bei elastischen Kollisionen

Nachdem nun Gleichungen für die Endgeschwindigkeiten beider Teilchen verfügbar sind, ist es an der Zeit, einige spezielle Situationen zu analysieren.

Zwei identische Massen

Dann m₁ = m_zwei = m Y:

v₁ = u_zwei

v_zwei = u₁

Die Partikel tauschen nach der Kollision einfach ihre Geschwindigkeiten aus.

Zwei identische Massen, von denen eine zunächst in Ruhe war

Nochmal  m₁ = m_zwei = m und unter der Annahme, dass oder₁ = 0:

v₁ = u_zwei

v_zwei = 0

Nach der Kollision erreicht das ruhende Teilchen die gleiche Geschwindigkeit wie das sich bewegende Teilchen, und dies stoppt wiederum.

Zwei verschiedene Massen, eine davon zunächst in Ruhe

In diesem Fall nehmen wir das an oder₁ = 0, aber die Massen sind unterschiedlich:

Was, wenn m₁ ist viel größer als m_zwei?

Es kommt vor, dass m₁ ist noch in Ruhe und m_zwei kehrt so schnell zurück, wie es getroffen hat.

Restitutionskoeffizient oder Huygens-Newton-Regel

Zuvor wurde die folgende Beziehung zwischen den Geschwindigkeiten für zwei Objekte in elastischer Kollision abgeleitet: oder₁ - oder_zwei = v_zwei -  v₁. Diese Unterschiede sind die relativen Geschwindigkeiten vor und nach der Kollision. Im Allgemeinen gilt für eine Kollision Folgendes:

oder₁ - oder_zwei = - (v₁ -  v_zwei)

Das Konzept der Relativgeschwindigkeit wird am besten geschätzt, wenn sich der Leser vorstellt, dass er sich auf einem der Partikel befindet, und von dieser Position aus die Geschwindigkeit beobachtet, mit der sich das andere Partikel bewegt. Die obige Gleichung wird folgendermaßen umgeschrieben:

Gelöste Übungen

-Gelöste Übung 1

Eine Billardkugel bewegt sich mit 30 cm / s nach links und kollidiert frontal mit einer anderen identischen Kugel, die sich mit 20 cm / s nach rechts bewegt. Die beiden Kugeln haben die gleiche Masse und die Kollision ist perfekt elastisch. Ermitteln der Geschwindigkeit jedes Balls nach dem Aufprall.

Lösung

oder₁ = -30 cm / s

oder_zwei = +20 cm / s

Es ist der Sonderfall, in dem zwei identische Massen in einer Dimension elastisch kollidieren, daher werden die Geschwindigkeiten ausgetauscht.

v₁ = +20 cm / s

v_zwei = -30 cm / s

-Übung gelöst 2

Der Restitutionskoeffizient eines Balls, der vom Boden abprallt, beträgt 0,82. Wenn es aus der Ruhe fällt, welchen Bruchteil seiner ursprünglichen Höhe erreicht der Ball nach einmaligem Abprallen? Und nach 3 Bounces?

Lösung

Der Boden kann Objekt 1 in der Restitutionskoeffizientengleichung sein. Und es bleibt immer in Ruhe, so dass:

Mit dieser Geschwindigkeit springt es:

Das + -Zeichen zeigt an, dass es sich um eine aufsteigende Geschwindigkeit handelt. Und demnach erreicht der Ball eine maximale Höhe von:

Jetzt kehrt es mit einer Geschwindigkeit der gleichen Größe, aber dem entgegengesetzten Vorzeichen, wieder auf den Boden zurück:

Dies erreicht eine maximale Höhe von:

Kommen Sie zurück auf den Boden mit:

Aufeinanderfolgende Sprünge

Jedes Mal, wenn der Ball springt und steigt, multiplizieren Sie die Geschwindigkeit erneut mit 0,82:

Inzwischen h₃ beträgt etwa 30% von h_oder. Was wäre die Höhe bis zum 6. Sprung ohne die Notwendigkeit, so detaillierte Berechnungen wie die vorherigen durchzuführen??

Würde h₆ = 0,82¹² h_oder = 0,092 h_oder oder nur 9% von h_oder.

-Übung gelöst 3

Ein 300-g-Block bewegt sich mit 50 cm / s nach Norden und kollidiert mit einem 200-g-Block mit 100 cm / s in Richtung Süden. Angenommen, der Stoßdämpfer ist perfekt elastisch. Finden Sie die Geschwindigkeiten nach dem Aufprall.

Daten

m₁ = 300 g; oder₁ = + 50 cm / s

m_zwei = 200 g; oder_zwei = -100 cm / s

-Übung gelöst 4

Eine Masse von m wird freigesetzt₁ = 4 kg vom angegebenen Punkt auf der reibungsfreien Spur bis zur Kollision mit m_zwei = 10 kg in Ruhe. Wie hoch steigt m?₁ nach der Kollision?

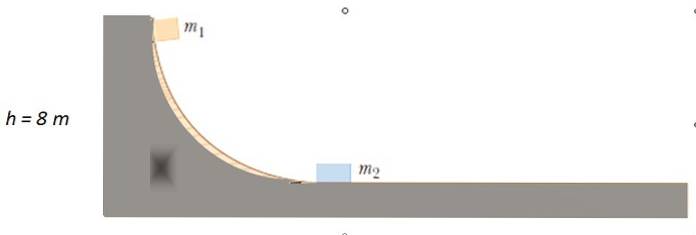
Lösung

Da es keine Reibung gibt, wird mechanische Energie erhalten, um die Geschwindigkeit zu finden oder₁ mit was m₁ Auswirkungen  m_zwei. Anfangs ist die kinetische Energie 0, da m₁ Teil der Ruhe. Wenn es sich auf der horizontalen Fläche bewegt, hat es keine Höhe, daher ist die potentielle Energie 0.

mgh = ½ mu₁ ^zwei

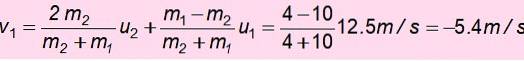
oder_zwei = 0

Nun ist die Geschwindigkeit von m₁ nach der Kollision:

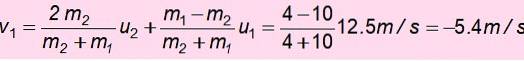
Das negative Vorzeichen bedeutet, dass es zurückgegeben wurde. Mit dieser Geschwindigkeit steigt es an und die mechanische Energie bleibt wieder erhalten, um zu finden h ', die Höhe, auf die Sie nach dem Absturz aufsteigen können:

½ mv₁^zwei = mgh '

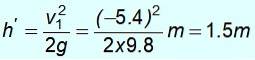
Beachten Sie, dass es in 8 m Höhe nicht zum Startpunkt zurückkehrt. Es hat nicht genug Energie, weil die Masse einen Teil ihrer kinetischen Energie gab m_1.

Verweise

1. Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6^th. Ed Prentice Hall. 175-181
2. Rex, A. 2011. Grundlagen der Physik. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Grundlagen der Physik. 9^{n / A} Lernen einbinden. 172-182
4. Tipler, P. (2006) Physik für Wissenschaft und Technologie. 5. Aufl. Band 1. Editorial Reverté. 217-238
5. Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. MacGraw Hill. 185-195