
Chi-Quadrat (χ²) -Verteilung, wie man sie berechnet, Beispiele
Der Beweis Chi im Quadrat oder Chi-Quadrat (χzwei, Dabei ist χ der griechische Buchstabe „Chi“.) wird verwendet, um das Verhalten einer bestimmten Variablen zu bestimmen und auch, wenn Sie wissen möchten, ob zwei oder mehr Variablen statistisch unabhängig sind.
Um das Verhalten einer Variablen zu überprüfen, wird der durchzuführende Test aufgerufen Chi-Quadrat-Fit-Test. Um herauszufinden, ob zwei oder mehr Variablen statistisch unabhängig sind, wird der Test aufgerufen Chi-Quadrat der Unabhängigkeit, auch genannt Kontingenz.
Diese Tests sind Teil der statistischen Entscheidungstheorie, in der eine Population untersucht und Entscheidungen darüber getroffen werden, wobei eine oder mehrere daraus entnommene Proben analysiert werden. Dies erfordert bestimmte Annahmen über die aufgerufenen Variablen Hypothese, was wahr sein kann oder nicht.
Es gibt einige Tests, um diese Vermutungen gegenüberzustellen und festzustellen, welche innerhalb eines bestimmten Vertrauensbereichs gültig sind, einschließlich des Chi-Quadrat-Tests, mit dem zwei und mehr Populationen verglichen werden können..
Wie wir sehen werden, werden normalerweise zwei Arten von Hypothesen über einen Populationsparameter in zwei Stichproben aufgestellt: die Nullhypothese, genannt H.oder (die Proben sind unabhängig) und die alternative Hypothese, bezeichnet als H.1, (die Stichproben sind korreliert), was das Gegenteil davon ist.
Artikelverzeichnis
- 1 Wann wird der Chi-Quadrat-Test verwendet??
- 1.1 Bedingungen für die Anwendung
- 2 Chi-Quadrat-Verteilung
- 2.1 Freiheitsgrade
- 2.2 Formulierung von Hypothesen
- 3 Wie berechnet sich die Chi-Quadrat-Statistik??
- 3.1 Abnahmekriterien für Ho
- 4 Berechnungsbeispiel
- 5 Referenzen
Wann wird der Chi-Quadrat-Test verwendet??
Der Chi-Quadrat-Test wird auf Variablen angewendet, die Eigenschaften wie Geschlecht, Familienstand, Blutgruppe, Augenfarbe und Präferenzen verschiedener Typen beschreiben.
Der Test ist gedacht, wenn Sie:
-Überprüfen, ob eine Verteilung zur Beschreibung einer aufgerufenen Variablen geeignet ist Güte der Anpassung. Mit dem Chi-Quadrat-Test kann festgestellt werden, ob zwischen der ausgewählten theoretischen Verteilung und der beobachteten Häufigkeitsverteilung signifikante Unterschiede bestehen..
-Wissen, ob zwei Variablen X und Y vom statistischen Standpunkt unabhängig sind. Dies ist bekannt als Unabhängigkeitstest.
Da der Chi-Quadrat-Test auf qualitative oder kategoriale Variablen angewendet wird, ist er in den Sozialwissenschaften, im Management und in der Medizin weit verbreitet..
Bedingungen für die Anwendung
Es gibt zwei wichtige Voraussetzungen, um es richtig anzuwenden:
-Die Daten müssen in Frequenzen gruppiert werden.
-Die Stichprobe muss groß genug sein, damit die Chi-Quadrat-Verteilung gültig ist. Andernfalls wird ihr Wert überschätzt und die Nullhypothese wird abgelehnt, wenn dies nicht der Fall sein sollte..
Die allgemeine Regel lautet, dass eine Frequenz mit einem Wert unter 5 in den gruppierten Daten nicht verwendet wird. Wenn mehr als eine Frequenz kleiner als 5 ist, müssen sie zu einer kombiniert werden, um eine Frequenz mit einem numerischen Wert größer als 5 zu erhalten.
Chi-Quadrat-Verteilung
χzwei es ist eine kontinuierliche Verteilung der Wahrscheinlichkeiten. Tatsächlich gibt es je nach Parameter unterschiedliche Kurven k namens Freiheitsgrade der Zufallsvariablen.
Seine Eigenschaften sind:
-Die Fläche unter der Kurve ist gleich 1.
-Die Werte von χzwei Sie sind positiv.
-Die Verteilung ist asymmetrisch, das heißt, sie ist voreingenommen.
Freiheitsgrade
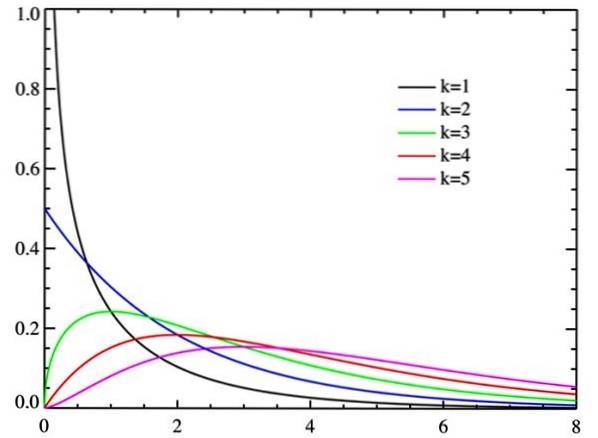
Mit zunehmenden Freiheitsgraden tendiert die Chi-Quadrat-Verteilung zur Normalität, wie aus der Abbildung ersichtlich ist.
Für eine gegebene Verteilung werden die Freiheitsgrade durch die bestimmt Kontingenztabelle, In dieser Tabelle werden die beobachteten Häufigkeiten der Variablen aufgezeichnet.
Wenn ein Tisch hat F. Zeilen und c Spalten, der Wert von k es ist:
k = (f - 1) ⋅ (c - 1)
Formulierung von Hypothesen
Wenn der Chi-Quadrat-Test passt, werden die folgenden Hypothesen formuliert:
-H.oder: Die Variable X hat eine Wahrscheinlichkeitsverteilung f (x) mit den spezifischen Parametern y1, Y.zwei…, Y.p
-H.1: X hat eine andere Wahrscheinlichkeitsverteilung.
Die in der Nullhypothese angenommene Wahrscheinlichkeitsverteilung kann beispielsweise die bekannte Normalverteilung sein, und die Parameter wären der Mittelwert μ und die Standardabweichung σ.
Darüber hinaus wird die Nullhypothese mit einem bestimmten Signifikanzniveau bewertet, dh einem Maß für den Fehler, der begangen würde, wenn er als wahr abgelehnt würde.
Normalerweise wird dieser Wert auf 1%, 5% oder 10% eingestellt. Je niedriger er ist, desto zuverlässiger ist das Testergebnis..
Und wenn der Chi-Quadrat-Kontingenztest verwendet wird, der, wie gesagt, dazu dient, die Unabhängigkeit zwischen zwei Variablen X und Y zu überprüfen, lauten die Hypothesen:
-H.oder: Die Variablen X und Y sind unabhängig.
-H.1: X und Y sind abhängig.
Auch hier muss ein Signifikanzniveau angegeben werden, um das Maß des Fehlers bei der Entscheidung zu kennen..
Wie berechnet sich die Chi-Quadrat-Statistik??
Die Chi-Quadrat-Statistik wird wie folgt berechnet:

Die Summierung wird von der ersten Klasse i = 1 bis zur letzten Klasse durchgeführt, die i = k ist.
Was ist mehr:
-F.oder ist eine beobachtete Frequenz (stammt aus den erhaltenen Daten).
-F.und ist die erwartete oder theoretische Häufigkeit (muss aus den Daten berechnet werden).
Um die Nullhypothese zu akzeptieren oder abzulehnen, berechnen wir χzwei für die beobachteten Daten und verglichen mit einem aufgerufenen Wert kritisches Chi-Quadrat, das hängt von den Freiheitsgraden ab k und das Signifikanzniveau α::
χzweikritisch = χzweik, α
Wenn wir zum Beispiel den Test mit einem Signifikanzniveau von 1% durchführen wollen, dann ist α = 0,01, wenn es mit 5% sein soll, dann ist α = 0,05 und so weiter. Wir definieren p, den Parameter der Verteilung, als:
p = 1 - α
Diese kritischen Chi-Quadrat-Werte werden durch Tabellen bestimmt, die den kumulativen Flächenwert enthalten. Zum Beispiel ist für k = 1, was 1 Freiheitsgrad darstellt, und α = 0,05, was p = 1 - 0,05 = 0,95 entspricht, der Wert von χzwei ist 3.841.

H Akzeptanzkriterienoder
Das Kriterium für die Annahme von H.oder es ist:
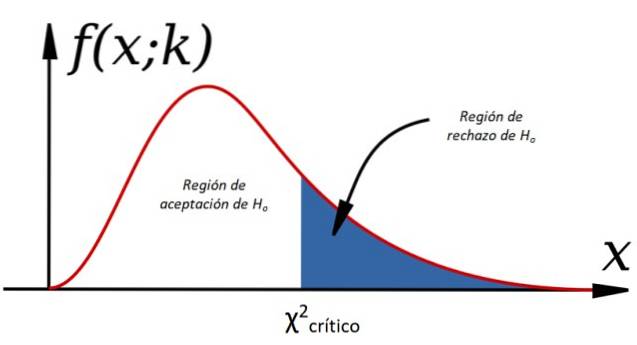
-Ja χzwei < χzweikritisch H wird akzeptiertoder, Andernfalls wird es abgelehnt (siehe Abbildung 1)..
Berechnungsbeispiel
In der folgenden Anwendung wird der Chi-Quadrat-Test als Unabhängigkeitstest verwendet.
Angenommen, die Forscher möchten wissen, ob die Präferenz für schwarzen Kaffee mit dem Geschlecht der Person zusammenhängt, und geben die Antwort mit einem Signifikanzniveau von α = 0,05 an.
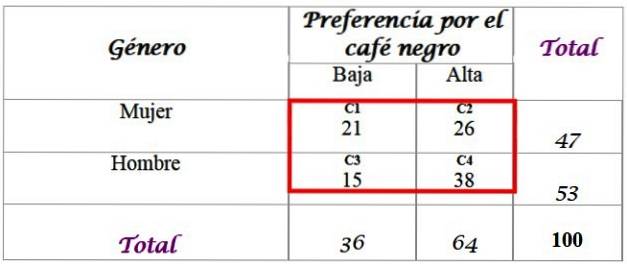
Hierzu steht eine Stichprobe von 100 Befragten und deren Antworten zur Verfügung:
Schritt 1
Stellen Sie die Hypothesen auf:
-H.oder: Geschlecht und Präferenz für schwarzen Kaffee sind unabhängig.
-H.1: Der Geschmack für schwarzen Kaffee hängt vom Geschlecht der Person ab.
Schritt 2
Berechnen Sie die erwarteten Häufigkeiten für die Verteilung, für die die in der letzten Zeile und in der rechten Spalte der Tabelle hinzugefügten Summen erforderlich sind. Jede Zelle im roten Feld hat einen erwarteten Wert F.und, Dies wird berechnet, indem die Summe Ihrer Zeile F mit der Summe Ihrer Spalte C multipliziert wird, geteilt durch die Summe der Stichprobe N:
F.und = (F x C) / N.
Die Ergebnisse sind für jede Zelle wie folgt:
-C1: (36 × 47) / 100 = 16,92
-C2: (64 × 47) / 100 = 30,08
-C3: (36 × 53) / 100 = 19,08
-C4: (64 × 53) / 100 = 33,92
Schritt 3
Als nächstes muss die Chi-Quadrat-Statistik für diese Verteilung gemäß der angegebenen Formel berechnet werden:

Schritt 4
Bestimmen Sie χzweikritisch, In dem Wissen, dass sich die aufgezeichneten Daten in f = 2 Zeilen und c = 2 Spalten befinden, beträgt die Anzahl der Freiheitsgrade:
k = (2-1) ⋅ (2-1) = 1.
Das heißt, wir müssen in der oben gezeigten Tabelle nach dem Wert von χ suchenzweik, α = χzwei1; 0,05 , welches ist:
χzweikritisch = 3,841
Schritt 5
Vergleichen Sie die Werte und entscheiden Sie:
χzwei = 2,9005
χzweikritisch = 3,841
Da χzwei < χzweikritisch Die Nullhypothese wird akzeptiert und es wird der Schluss gezogen, dass die Präferenz für schwarzen Kaffee nicht mit dem Geschlecht der Person zusammenhängt, mit einem Signifikanzniveau von 5%.
Verweise
- Chi-Quadrat-Test für Unabhängigkeit. Wiederhergestellt von: saylordotorg.github.io.
- Med Wave. Statistik für die Gesundheitswissenschaften: der Chi-Quadrat-Test. Wiederhergestellt von: medwave.cl.
- Wahrscheinlichkeiten und Statistiken. Chi-Quadrat-Anpassungstest. Wiederhergestellt von: probayestadistica.com.
- Triola, M. 2012. Elementare Statistik. 11 .. Auflage. Addison Wesley.
- UNAM. Chi-Quadrat-Test. Wiederhergestellt von: asesorias.cuautitlan2.unam.mx.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.