
Axiale Belastung, wie sie berechnet und Übungen gelöst werden
Das axiale Belastung Es ist die Kraft, die parallel zur Symmetrieachse eines Elements gerichtet ist, aus dem eine Struktur besteht. Die axiale Kraft oder Last kann Spannung oder Kompression sein. Wenn die Wirkungslinie der Axialkraft mit der Symmetrieachse übereinstimmt, die durch den Schwerpunkt des betrachteten Elements verläuft, spricht man von einer konzentrischen Axialkraft oder -kraft.
Im Gegenteil, wenn es sich um eine Axialkraft oder Last parallel zur Symmetrieachse handelt, deren Wirkungslinie jedoch nicht auf der Achse selbst liegt, handelt es sich um eine exzentrische Axialkraft.
-
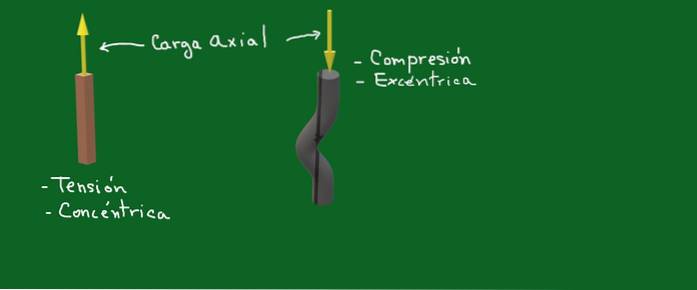
Abbildung 1. Axiale Belastung. Quelle: selbst gemacht
In Abbildung 1 stehen die gelben Pfeile für Axialkräfte oder Lasten. In einem Fall handelt es sich um eine konzentrische Zugkraft und im anderen Fall handelt es sich um eine exzentrische Druckkraft.
Die Maßeinheit für die axiale Belastung im internationalen SI-System ist Newton (N). Aber auch andere Krafteinheiten wie Kilogrammkraft (kg-f) und Pfundkraft (lb-f) werden häufig verwendet..
Artikelverzeichnis
- 1 Wie wird es berechnet??
- 1.1 Verhältnis der axialen Belastung zur Normalspannung
- 2 Gelöste Übungen
- 2.1 -Übung 1
- 2.2 -Übung 2
- 3 Referenzen
Wie wird es berechnet??
Um den Wert der Axialkraft in den Elementen einer Struktur zu berechnen, müssen die folgenden Schritte ausgeführt werden:
- Machen Sie das Kraftdiagramm für jedes Element.
- Wenden Sie die Gleichungen an, die ein Translationsgleichgewicht gewährleisten, dh, dass die Summe aller Kräfte Null ist.
- Betrachten Sie die Gleichung der Drehmomente oder Momente, damit das Rotationsgleichgewicht erfüllt ist. In diesem Fall muss die Summe aller Drehmomente Null sein.
- Berechnen Sie die Kräfte und identifizieren Sie die Kräfte oder axialen Belastungen in jedem der Elemente.
Verhältnis von Axialkraft zu Normalspannung
Die durchschnittliche Normalspannung ist definiert als das Verhältnis der axialen Belastung geteilt durch die Querschnittsfläche. Die Einheiten der normalen Anstrengung im Internationalen System S.I. Sie sind Newton über Quadratmeter (N / m²) oder Pascal (Pa). Die folgende Abbildung 2 zeigt das Konzept der Normalspannung zur Verdeutlichung..
-
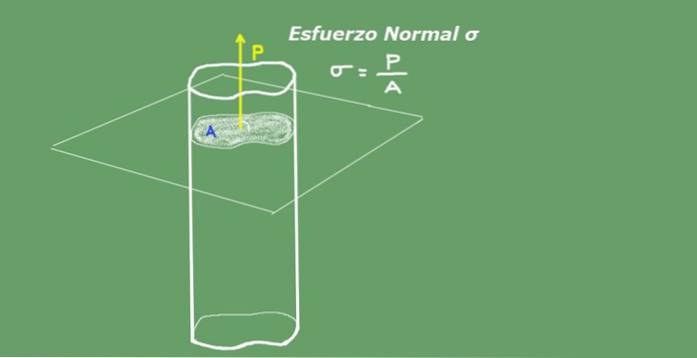
Abbildung 2. Normaler Stress. Quelle: selbst gemacht.
Gelöste Übungen
-Übung 1
Betrachten Sie eine zylindrische Betonsäule mit der Höhe h und dem Radius r. Angenommen, die Dichte des Betons ist ρ. Die Säule trägt keine zusätzliche Last außer ihrem eigenen Gewicht und wird auf einer rechteckigen Basis getragen.
- Ermitteln Sie den Wert der axialen Belastung an den Punkten A, B, C und D, die sich an folgenden Positionen befinden: A am Fuß der Säule, B a ⅓ der Höhe h, C a ⅔ der Höhe h und bis zum letzten D at der obere Rand der Spalte.
- Bestimmen Sie auch die durchschnittliche Normalspannung an jeder dieser Positionen. Nehmen Sie die folgenden Zahlenwerte: h = 3 m, r = 20 cm und ρ = 2250 kg / m³
-
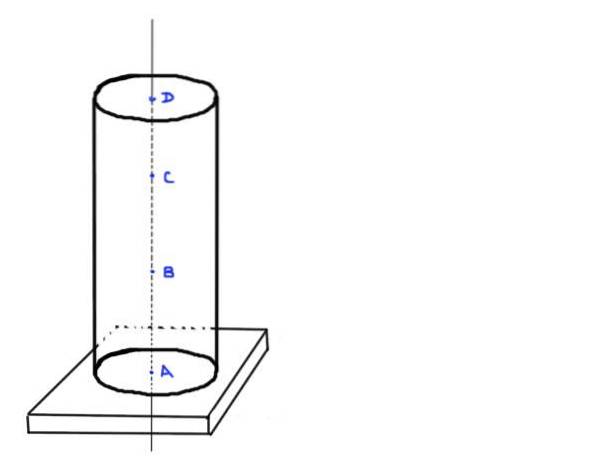
Abbildung 3. Zylindrische Säule. Quelle: selbst gemacht.
Lösung
Gesamtsäulengewicht
Das Gesamtgewicht W der Säule ist das Produkt ihrer Dichte multipliziert mit dem Volumen multipliziert mit der Erdbeschleunigung:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N.
Axiale Belastung in A.
Am Punkt A muss die Säule ihr volles Gewicht tragen, sodass die axiale Belastung an diesem Punkt die Kompression ist, die dem Gewicht der Säule entspricht:
PA = W = 8313 N.
Axiale Belastung bei B.
Nur ⅔ der Säule befindet sich auf Punkt B, daher ist die axiale Belastung an diesem Punkt die Kompression und ihr Wert ⅔ das Gewicht der Säule:
PB = ⅔ W = 5542 N.
Abbildung 3. Zylindersäule. Quelle: selbst gemacht.
Oberhalb von Position C befindet sich nur ⅓ der Säule, so dass die axiale Druckbelastung ⅓ des Eigengewichts beträgt:
PC = ⅓ W = 2771 N.
Axiale Belastung in D.
Schließlich wird der Punkt D, der das obere Ende der Säule darstellt, nicht belastet, sodass die Axialkraft an diesem Punkt Null ist..
PD = 0 N.
Normale Anstrengungen in jeder Position
Um die Normalspannung in jeder der Positionen zu bestimmen, muss der Querschnitt der Fläche A berechnet werden, der gegeben ist durch:
A = π ∙ r² = 0,126 m²
Auf diese Weise ist die Normalspannung in jeder der Positionen der Quotient zwischen der Axialkraft in jedem der Punkte geteilt durch die bereits berechnete Querschnittsfläche, die in dieser Übung für alle Punkte gleich ist, da es sich um a handelt Säule zylindrisch.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Übung 2
Die Abbildung zeigt eine Struktur aus zwei Balken, die wir AB und CB nennen werden. Die Stange AB wird am Ende A von einem Stift getragen und am anderen Ende durch einen anderen Stift B mit der anderen Stange verbunden.
In ähnlicher Weise wird die Stange CB am Ende C mittels eines Stifts und am Ende B mit dem Stift B, der sie mit der anderen Stange verbindet, abgestützt. Eine vertikale Kraft oder Last F wird auf Stift B ausgeübt, wie in der folgenden Abbildung gezeigt:
-
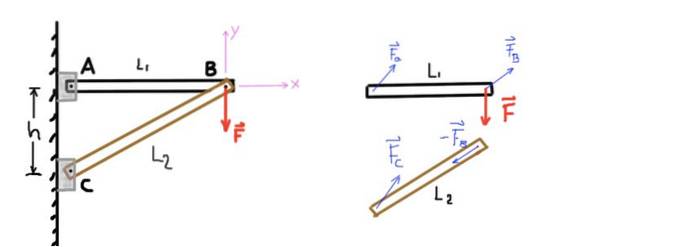
Abbildung 4. Zwei-Balken-Struktur und Freikörperdiagramm. Quelle: selbst gemacht.
Es sei angenommen, dass das Gewicht der Stangen vernachlässigbar ist, da die Kraft F = 500 kg-f viel größer ist als das Gewicht der Struktur. Der Abstand zwischen den Trägern A und C beträgt h = 1,5 m und die Länge der Stange AB beträgt L1 = 2 m. Bestimmen Sie die axiale Belastung jeder Stange und geben Sie an, ob es sich um eine axiale Druck- oder Zugbelastung handelt.
Lösung 2
Die Abbildung zeigt anhand eines Freikörperdiagramms die Kräfte, die auf jedes der Elemente der Struktur wirken. Das kartesische Koordinatensystem, mit dem die Kraftgleichgewichtsgleichungen erstellt werden, ist ebenfalls angegeben..
Drehmomente oder Momente werden am Punkt B berechnet und als positiv betrachtet, wenn sie vom Bildschirm weg zeigen (Z-Achse). Das Gleichgewicht der Kräfte und Drehmomente für jeden Stab ist:
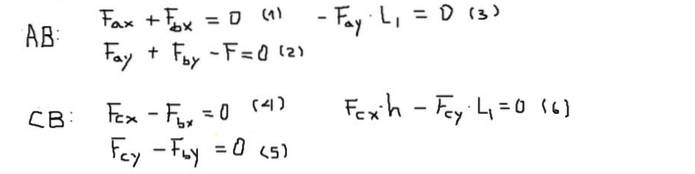
Als nächstes werden die Komponenten der Kräfte jeder der Gleichungen in der folgenden Reihenfolge gelöst:
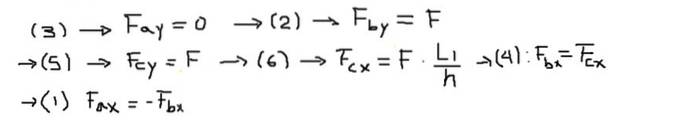
Schließlich werden die resultierenden Kräfte an den Enden jedes Balkens berechnet:
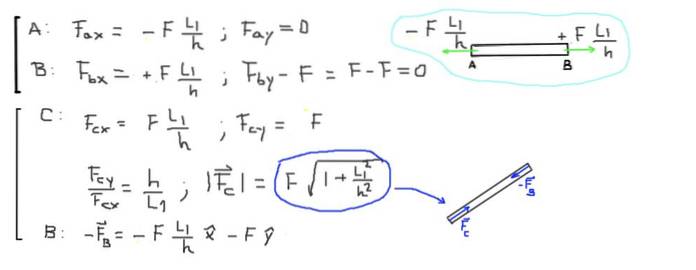
F L (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N.
Die Stange CB wird aufgrund der beiden an ihren Enden wirkenden Kräfte, die parallel zur Stange sind und in Richtung ihrer Mitte zeigen, unter Druck gesetzt. Die Größe der axialen Druckkraft in der Stange CB beträgt:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N.
Verweise
- Bier F… Mechanik der Materialien. 5 .. Auflage. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Materialmechanik. Achte Ausgabe. Prentice Hall. 2011. 3-60.
- Gere J. Mechanik der Werkstoffe. Achte Ausgabe. Lernen einbinden. 4-220.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6. Aufl. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Anmerkungen zur allgemeinen Physik. UNAM. 87-98.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.