Das normaler Vektor ist diejenige, die die Richtung senkrecht zu einer betrachteten geometrischen Einheit definiert, die beispielsweise eine Kurve, eine Ebene oder eine Oberfläche sein kann.
Es ist ein sehr nützliches Konzept bei der Positionierung eines sich bewegenden Partikels oder einer Oberfläche im Raum. In der folgenden Grafik ist zu sehen, wie der Normalenvektor zu einer beliebigen Kurve aussieht C.::
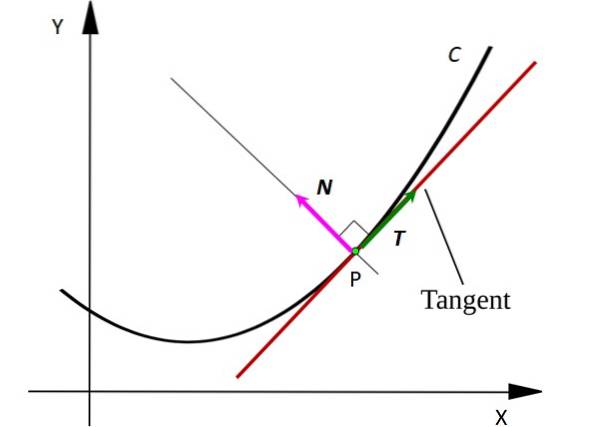
Betrachten Sie einen Punkt P auf der Kurve C. Der Punkt kann ein sich bewegendes Teilchen darstellen, das sich entlang eines C-förmigen Pfades bewegt. Die Tangentenlinie zur Kurve am Punkt P ist rot gezeichnet..
Beachten Sie, dass der Vektor T. ist an jedem Punkt tangential zu C, während der Vektor N. ist senkrecht zu T. y zeigt auf den Mittelpunkt eines imaginären Kreises, dessen Bogen ein Segment von C ist. Vektoren werden im gedruckten Text fett gedruckt, um sie von anderen Nicht-Vektor-Größen zu unterscheiden.
Der Vektor T. es zeigt immer an, wohin sich das Teilchen bewegt, daher zeigt es seine Geschwindigkeit an. Stattdessen der Vektor N. zeigt immer in die Richtung, in die sich das Teilchen dreht, auf diese Weise zeigt es die Konkavität der Kurve C an.
Artikelverzeichnis
Der Normalvektor ist nicht notwendigerweise ein Einheitsvektor, dh ein Vektor, dessen Modul 1 ist, aber wenn ja, wird er aufgerufen normaler Einheitsvektor.
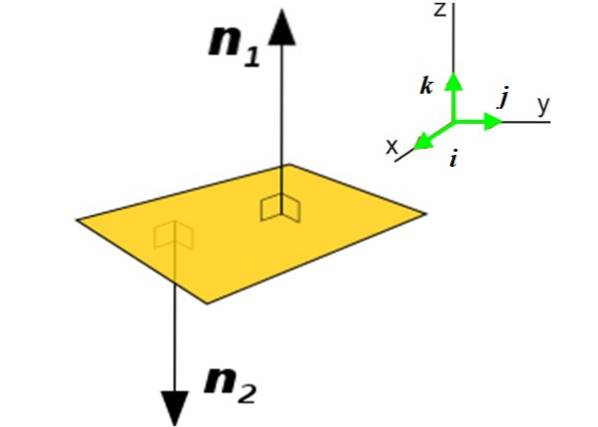
In vielen Anwendungen ist es erforderlich, den Normalenvektor zu einer Ebene anstelle einer Kurve zu kennen. Dieser Vektor zeigt die Ausrichtung der Ebene im Raum. Betrachten Sie zum Beispiel das Flugzeug P. (gelb) der Figur:
Es gibt zwei normale Vektoren zu dieser Ebene: n1 Y. nzwei. Die Verwendung des einen oder anderen hängt von dem Kontext ab, in dem sich die Ebene befindet. Das Erhalten des Normalenvektors zu einer Ebene ist sehr einfach, wenn Sie seine Gleichung kennen:
ax + by + cz + d = 0, mit zu, b, c Y. d reale Nummern.
Nun, ein normaler Vektor zu dieser Ebene ist gegeben durch:
N. = a ich + b j + c k
Hier der Vektor N. Sie wird als Einheitsvektoren und senkrecht zueinander ausgedrückt ich, j Y. k, entlang der drei Richtungen gerichtet, die den Raum bestimmen X und Z., siehe Abbildung 2 rechts.
Ein sehr einfaches Verfahren zum Finden des normalen Vektors nutzt die Eigenschaften des Vektorprodukts zwischen zwei Vektoren.
Bekanntlich bestimmen drei verschiedene Punkte, die nicht kollinear miteinander sind, eine Ebene P. Nun ist es möglich, zwei Vektoren zu erhalten oder Y. v das gehört zu der Ebene mit diesen drei Punkten.
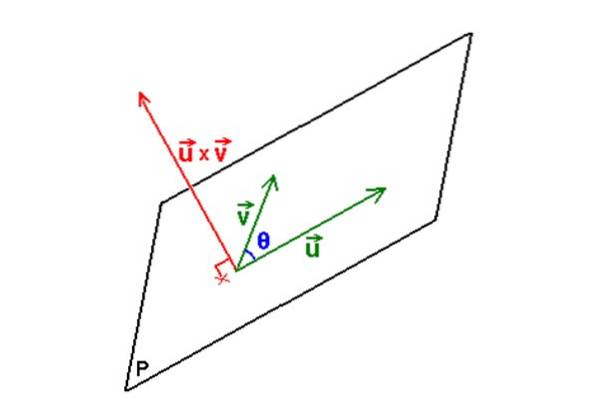
Sobald Sie die Vektoren haben, wird die Vektorprodukt oder x v ist eine Operation, deren Ergebnis wiederum ein Vektor ist, der die Eigenschaft hat, senkrecht zu der durch bestimmten Ebene zu sein oder Y. v.
Bekannt als dieser Vektor, wird er als bezeichnet N., und daraus wird es möglich sein, die Gleichung der Ebene dank der im vorhergehenden Abschnitt angegebenen Gleichung zu bestimmen:
N. = oder x v
Die folgende Abbildung zeigt das beschriebene Verfahren:
Finden Sie die Gleichung der Ebene, die durch die Punkte A (2,1,3) bestimmt wird; B (0,1,1); C (4,2,1).
Diese Übung veranschaulicht das oben beschriebene Verfahren. Mit 3 Punkten wird einer von ihnen als gemeinsamer Ursprung von zwei Vektoren ausgewählt, die zu der durch diese Punkte definierten Ebene gehören. Beispielsweise wird Punkt A als Ursprung festgelegt und die Vektoren werden konstruiert AB Y. AC.
Der Vektor AB ist der Vektor, dessen Ursprung Punkt A und dessen Endpunkt Punkt B ist. Die Koordinaten des Vektors AB werden bestimmt, indem jeweils die Koordinaten von B von den Koordinaten von A subtrahiert werden:
AB = (0-2) ich + (1-1) j + (1-3) k = -2ich + 0j -zwei k
Wir gehen genauso vor, um den Vektor zu finden AC::
AC = (4-2) ich + (2-1) j + (1-3) k = 2ich + j -zwei k
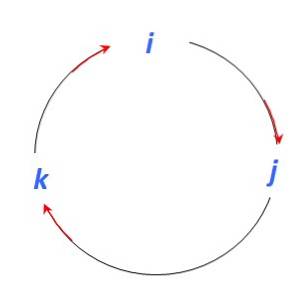
Es gibt verschiedene Verfahren, um das Vektorprodukt zwischen zwei Vektoren zu finden. In diesem Beispiel wird eine mnemonische Prozedur verwendet, bei der anhand der folgenden Abbildung die Vektorprodukte zwischen den Einheitsvektoren ermittelt werden ich, j Y. k:
Zunächst ist zu beachten, dass die Vektorprodukte zwischen parallelen Vektoren null sind, daher:
ich x ich = 0; j x j = 0; k x k = 0
Und da das Vektorprodukt ein weiterer Vektor senkrecht zu den beteiligten Vektoren ist, haben wir beim Bewegen in Richtung des roten Pfeils:
ich x j = k ;; j x k = ich;; k x ich = j
Wenn Sie sich in die entgegengesetzte Richtung zum Pfeil bewegen müssen, fügen Sie ein Zeichen (-) hinzu:
j x ich = - k;; k x j = -ich;; ich x k = -j
Insgesamt ist es möglich, 9 Vektorprodukte mit den Einheitsvektoren herzustellen ich, j Y. k, von denen 3 null sein werden.
AB x AC = (-2ich + 0j -zwei k) x (2ich + j -zwei k) = -4 (ich x ich) -zwei (ich x j) +4 (ich x k) +0 (j x ich) + 0 (j x j) - 0 (j x k) - 4 (k x ich) -zwei (k x j) + 4 (k x k) = -2k-4j-4j+zweiich = 2ich -8j-zweik
Der Vektor N wurde durch das zuvor berechnete Vektorprodukt bestimmt:
N. = zweiich -8j-zweik
Daher ist a = 2, b = -8, c = -2, die gesuchte Ebene ist:
ax + by + cz + d = 0 → 2x-8y-2z + d = 0
Der Wert von d. Dies ist einfach, wenn die Werte der verfügbaren Punkte A, B oder C in der Gleichung der Ebene eingesetzt werden. Wählen Sie zum Beispiel C:
x = 4; y = 2; z = 1
Überreste:
2,4 - 8,2 - 2,1 + d = 0
-10 + d = 0
d = 10
Kurz gesagt, die gesuchte Karte lautet:
2x-8y-2z +10 = 0
Der neugierige Leser mag sich fragen, ob das gleiche Ergebnis erzielt worden wäre, wenn er es nicht getan hätte AB x AC sie hätten sich entschieden zu bewirken AC x AB. Die Antwort lautet: Ja, die durch diese drei Punkte bestimmte Ebene ist eindeutig und weist zwei Normalenvektoren auf, wie in Abbildung 2 dargestellt.
Für den als Ursprung der Vektoren ausgewählten Punkt gibt es kein Problem bei der Auswahl eines der beiden anderen.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.