
Laplace-Transformationsdefinition, Geschichte und wofür sie ist
Das Laplace-Transformation In den letzten Jahren war es unter anderem in den Bereichen Ingenieurwesen, Mathematik und Physik von großer Bedeutung, da es nicht nur von großem theoretischen Interesse ist, sondern auch eine einfache Möglichkeit bietet, Probleme aus Wissenschaft und Technik zu lösen..
Ursprünglich wurde die Laplace-Transformation von Pierre-Simón Laplace in seiner Studie zur Wahrscheinlichkeitstheorie vorgestellt und zunächst als mathematisches Objekt von rein theoretischem Interesse behandelt..

Aktuelle Anwendungen entstehen, wenn verschiedene Mathematiker versuchten, die von Heaviside beim Studium der Gleichungen der elektromagnetischen Theorie verwendeten "Betriebsregeln" formal zu rechtfertigen..
Artikelverzeichnis
- 1 Definition
- 1.1 Beispiele
- 1.2 Satz (ausreichende Existenzbedingungen)
- 1.3 Laplace-Transformation einiger Grundfunktionen
- 2 Geschichte
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 Eigenschaften
- 3.1 Linearität
- 3.2 Erster Übersetzungssatz
- 3.3 Zweiter Übersetzungssatz
- 3.4 Skalenänderung
- 3.5 Laplace-Transformation von Derivaten
- 3.6 Laplace-Transformation von Integralen
- 3.7 Multiplikation mit tn
- 3.8 Division durch t
- 3.9 Periodische Funktionen
- 3.10 Verhalten von F (s) als s gegen unendlich
- 4 Inverse Transformationen
- 4.1 Übung
- 5 Anwendungen der Laplace-Transformation
- 5.1 Differentialgleichungen
- 5.2 Differentialgleichungssysteme
- 5.3 Mechanik und Stromkreise
- 6 Referenzen
Definition
Sei f eine für t ≥ 0 definierte Funktion. Die Laplace-Transformation ist wie folgt definiert:
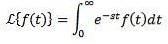
Die Laplace-Transformation soll existieren, wenn das vorherige Integral konvergiert, andernfalls wird gesagt, dass die Laplace-Transformation nicht existiert.
Im Allgemeinen werden Kleinbuchstaben verwendet, um die zu transformierende Funktion zu bezeichnen, und der Großbuchstabe entspricht seiner Transformation. Auf diese Weise haben wir:
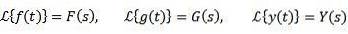
Beispiele
Betrachten Sie die konstante Funktion f (t) = 1. Wir haben, dass ihre Transformation ist:
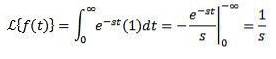
Wann immer das Integral konvergiert, dh wann immer s> 0. Andernfalls s < 0, la integral diverge.
Sei g (t) = t. Seine Laplace-Transformation ist gegeben durch
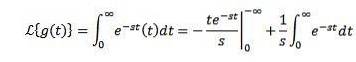
Indem Sie sich nach Teilen integrieren und wissen, dass Sie-st tendiert zu 0, wenn t gegen unendlich tendiert und s> 0, zusammen mit dem vorherigen Beispiel, das wir haben:
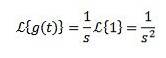
Die Transformation kann existieren oder nicht, zum Beispiel für die Funktion f (t) = 1 / t konvergiert das Integral, das seine Laplace-Transformation definiert, nicht und daher existiert seine Transformation nicht.
Die ausreichenden Bedingungen, um sicherzustellen, dass die Laplace-Transformation einer Funktion f existiert, sind, dass f in Teilen für t ≥ 0 stetig ist und eine exponentielle Ordnung aufweist.
Eine Funktion wird für t ≥ 0 als stückweise stetig bezeichnet, wenn für jedes Intervall [a, b] mit a> 0 eine endliche Anzahl von Punkten t vorliegtk, wobei f Diskontinuitäten aufweist und in jedem Teilintervall stetig ist [tk-1,tk]].
Andererseits wird gesagt, dass eine Funktion von exponentieller Ordnung c ist, wenn es reelle Konstanten M> 0, c und T> 0 gibt, so dass:
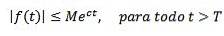
Als Beispiele haben wir f (t) = tzwei ist exponentiell, da | tzwei| < e3t für alle t> 0.
In formaler Weise haben wir den folgenden Satz
Satz (ausreichende Existenzbedingungen)
Wenn f eine teilkontinuierliche Funktion für t> 0 und von exponentieller Ordnung c ist, existiert die Laplace-Transformation für s> c.
Es ist wichtig anzumerken, dass dies eine Bedingung der Suffizienz ist, das heißt, es könnte der Fall sein, dass es eine Funktion gibt, die diese Bedingungen nicht erfüllt, und trotzdem existiert ihre Laplace-Transformation.
Ein Beispiel hierfür ist die Funktion f (t) = t-1/2 Dies ist für t ≥ 0 nicht stückweise stetig, aber seine Laplace-Transformation existiert.
Laplace-Transformation einiger Grundfunktionen
Die folgende Tabelle zeigt die Laplace-Transformationen der häufigsten Funktionen.

Geschichte
Die Laplace-Transformation verdankt ihren Namen Pierre-Simon Laplace, einem französischen Mathematiker und theoretischen Astronomen, der 1749 geboren wurde und 1827 starb. Sein Ruhm war so groß, dass er als Newton von Frankreich bekannt wurde.
1744 widmete Leonard Euler seine Studien Integralen mit der Form
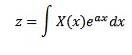
als Lösung gewöhnlicher Differentialgleichungen, aber er gab diese Untersuchung schnell auf. Später untersuchte auch Joseph Louis Lagrange, der Euler sehr bewunderte, diese Art von Integralen und bezog sie auf die Wahrscheinlichkeitstheorie.
1782, Laplace
1782 begann Laplace, diese Integrale als Lösungen für Differentialgleichungen zu untersuchen, und Historikern zufolge beschloss er 1785, das Problem neu zu formulieren, was später zu den Laplace-Transformationen führte, wie sie heute verstanden werden..
Nachdem es in das Gebiet der Wahrscheinlichkeitstheorie eingeführt worden war, war es für die damaligen Wissenschaftler von geringem Interesse und wurde nur als mathematisches Objekt von nur theoretischem Interesse angesehen..
Oliver Heaviside
Mitte des 19. Jahrhunderts entdeckte der englische Ingenieur Oliver Heaviside, dass Differentialoperatoren als algebraische Variablen behandelt werden können, wodurch Laplace-Transformationen ihre moderne Anwendung erhalten..
Oliver Heaviside war ein englischer Physiker, Elektrotechniker und Mathematiker, der 1850 in London geboren wurde und 1925 starb. Während er versuchte, Differentialgleichungsprobleme zu lösen, die auf die Schwingungstheorie angewendet wurden, und Laplace-Studien verwendete, begann er, die modernen Anwendungen von Laplace-Transformationen zu formen.
Die von Heaviside präsentierten Ergebnisse verbreiteten sich schnell in der damaligen wissenschaftlichen Gemeinschaft, aber da seine Arbeit nicht streng war, wurde er von den traditionelleren Mathematikern schnell kritisiert..
Die Nützlichkeit von Heavisides Arbeit bei der Lösung von Gleichungen in der Physik machte seine Methoden jedoch bei Physikern und Ingenieuren beliebt..
Trotz dieser Rückschläge und nach einigen Jahrzehnten fehlgeschlagener Versuche konnten zu Beginn des 20. Jahrhunderts die von Heaviside vorgegebenen Betriebsregeln streng begründet werden..
Diese Versuche trugen dank der Bemühungen verschiedener Mathematiker wie Bromwich, Carson und van der Pol Früchte..
Eigenschaften
Unter den Eigenschaften der Laplace-Transformation fallen folgende auf:
Linearität
Sei c1 und c2 konstant und f (t) und g (t) funktionieren, deren Laplace-Transformationen F (s) bzw. G (s) sind, dann haben wir:
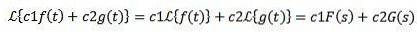
Aufgrund dieser Eigenschaft wird die Laplace-Transformation als linearer Operator bezeichnet.
Beispiel
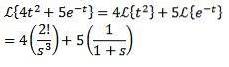
Erster Übersetzungssatz
Wenn es passiert, dass:
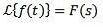
Und 'a' ist eine beliebige reelle Zahl, also:
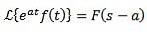
Beispiel
Da die Laplace-Transformation von cos (2t) = s / (s ^ 2 + 4) ist, dann:
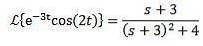
Zweiter Übersetzungssatz
Ja
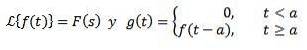
Dann
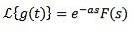
Beispiel
Wenn f (t) = t ^ 3, dann ist F (s) = 6 / s ^ 4. Und deshalb die Transformation von
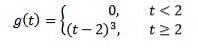
ist G (s) = 6e-2s/ s ^ 4
Skalenänderung
Ja
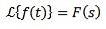
Und 'a' ist ein Real ungleich Null, das müssen wir
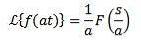
Beispiel
Da die Transformation von f (t) = sin (t) F (s) = 1 / (s ^ 2 + 1) ist, haben wir
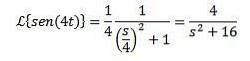
Laplace-Transformation von Derivaten
Wenn f, f ', f ", ..., f(n) sind stetig für t ≥ 0 und sind von exponentieller Ordnung und f(n)(t) ist dann für t ≥ 0 stückweise stetig
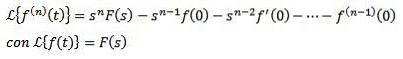
Laplace-Transformation von Integralen
Ja
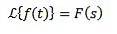
Dann
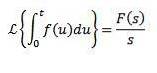
Multiplikation mit tn
Wenn wir müssen
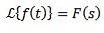
Dann
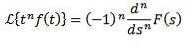
Division durch t
Wenn wir müssen
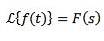
Dann
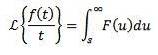
Periodische Funktionen
Sei f eine periodische Funktion mit der Periode T> 0, dh f (t + T) = f (t)
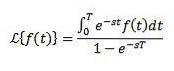
Das Verhalten von F (s) als s neigt zur Unendlichkeit
Wenn f in Teilen stetig und exponentiell ist und
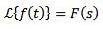
Dann
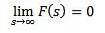
Inverse Transformationen
Wenn wir die Laplace-Transformation auf eine Funktion f (t) anwenden, erhalten wir F (s), die diese Transformation darstellt. Ebenso können wir sagen, dass f (t) die inverse Laplace-Transformation von F (s) ist und geschrieben wird als
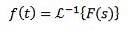
Wir wissen, dass die Laplace-Transformationen von f (t) = 1 und g (t) = t F (s) = 1 / s und G (s) = 1 / s sindzwei jeweils müssen wir also
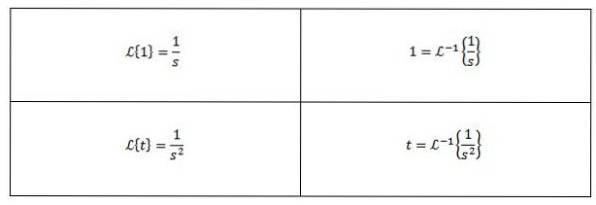
Einige übliche inverse Laplace-Transformationen sind wie folgt

Darüber hinaus ist die inverse Laplace-Transformation linear, das heißt, es ist wahr, dass
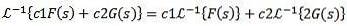
Übung
Finden
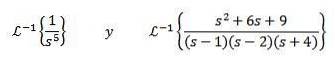
Um diese Übung zu lösen, müssen wir die Funktion F (s) mit einer der vorherigen Tabellen abgleichen. In diesem Fall multiplizieren und dividieren wir durch 4, wenn wir n + 1 = 5 nehmen und die Linearitätseigenschaft der inversen Transformation verwenden! Bekommen
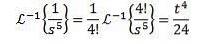
Für die zweite inverse Transformation wenden wir Teilbrüche an, um die Funktion F (s) und dann die Eigenschaft der Linearität neu zu schreiben und zu erhalten
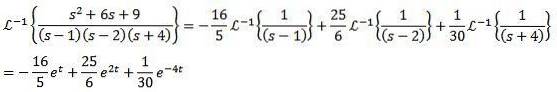
Wie wir aus diesen Beispielen sehen können, ist es üblich, dass die zu bewertenden Funktionen F (s) nicht genau mit einer der in der Tabelle angegebenen Funktionen übereinstimmen. In diesen Fällen reicht es, wie zu sehen ist, aus, die Funktion neu zu schreiben, bis die entsprechende Form erreicht ist.
Anwendungen der Laplace-Transformation
Differentialgleichung
Die Hauptanwendung von Laplace-Transformationen ist die Lösung von Differentialgleichungen.
Bei Verwendung der Transformationseigenschaft eines Derivats ist klar, dass
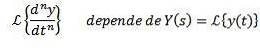
Und von den bei t = 0 bewerteten n-1-Derivaten.
Diese Eigenschaft macht die Transformation sehr nützlich, um Anfangswertprobleme zu lösen, bei denen Differentialgleichungen mit konstanten Koeffizienten beteiligt sind..
Die folgenden Beispiele zeigen, wie die Laplace-Transformation zum Lösen von Differentialgleichungen verwendet wird.
Beispiel 1
Angesichts des folgenden Anfangswertproblems
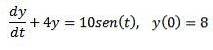
Verwenden Sie die Laplace-Transformation, um die Lösung zu finden.
Wir wenden die Laplace-Transformation auf jedes Mitglied der Differentialgleichung an
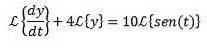
Durch die Eigenschaft der Transformation eines Derivats haben wir
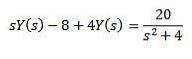
Indem wir alle Ausdrücke entwickeln und Y (s) löschen, bleiben wir zurück
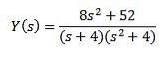
Verwenden Sie Teilbrüche, um die rechte Seite der Gleichung neu zu schreiben
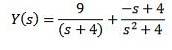
Schließlich ist es unser Ziel, eine Funktion y (t) zu finden, die die Differentialgleichung erfüllt. Die Verwendung der inversen Laplace-Transformation liefert das Ergebnis
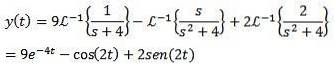
Beispiel 2
Lösen
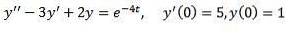
Wie im vorherigen Fall wenden wir die Transformation auf beiden Seiten der Gleichung an und trennen Term für Term.
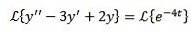
Auf diese Weise haben wir als Ergebnis
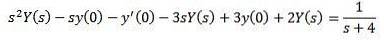
Ersetzen durch die angegebenen Anfangswerte und Auflösen nach Y (s)
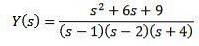
Mit einfachen Brüchen können wir die Gleichung wie folgt umschreiben
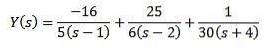
Und die Anwendung der inversen Laplace-Transformation liefert das Ergebnis
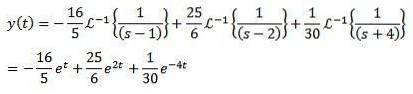
In diesen Beispielen könnten Sie zu dem falschen Schluss kommen, dass diese Methode nicht viel besser ist als herkömmliche Methoden zur Lösung von Differentialgleichungen..
Die Vorteile der Laplace-Transformation bestehen darin, dass Sie keine Parametervariation verwenden oder sich um die verschiedenen Fälle der Methode des unbestimmten Koeffizienten kümmern müssen..
Wenn wir Anfangswertprobleme mit dieser Methode lösen, verwenden wir von Anfang an die Anfangsbedingungen, sodass es nicht erforderlich ist, andere Berechnungen durchzuführen, um die bestimmte Lösung zu finden.
Differentialgleichungssysteme
Die Laplace-Transformation kann auch verwendet werden, um Lösungen für simultane gewöhnliche Differentialgleichungen zu finden, wie das folgende Beispiel zeigt.
Beispiel
Aussortieren
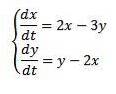
Mit den Anfangsbedingungen ist x (0) = 8 und y (0) = 3.
Wenn wir müssen
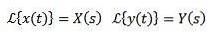
Dann
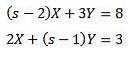
Das Lösen gibt uns das Ergebnis
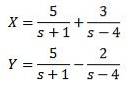
Und die inverse Laplace-Transformation anwenden, die wir haben
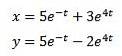
Mechanik und Stromkreise
Die Laplace-Transformation ist in der Physik von großer Bedeutung, sie hat hauptsächlich Anwendungen für Mechanik und elektrische Schaltkreise.
Ein einfacher Stromkreis besteht aus den folgenden Elementen
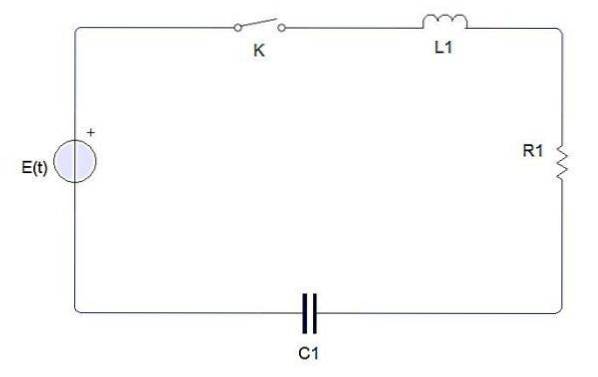
Ein Schalter, eine Batterie oder Quelle, eine Induktivität, ein Widerstand und ein Kondensator. Wenn der Schalter geschlossen ist, wird ein elektrischer Strom erzeugt, der mit i (t) bezeichnet wird. Die Kondensatorladung wird mit q (t) bezeichnet..
Nach Kirchhoffs zweitem Gesetz muss die von der Quelle E an den geschlossenen Stromkreis erzeugte Spannung gleich der Summe jedes Spannungsabfalls sein.
Der elektrische Strom i (t) steht in Beziehung zur Ladung q (t) am Kondensator durch i = dq / dt. Andererseits ist der Spannungsabfall in jedem der Elemente wie folgt definiert:
Der Spannungsabfall an einem Widerstand beträgt iR = R (dq / dt)
Der Spannungsabfall an einer Induktivität beträgt L (di / dt) = L (dzweiq / dtzwei)
Der Spannungsabfall an einem Kondensator beträgt q / C.
Mit diesen Daten und der Anwendung des zweiten Kirchhoffschen Gesetzes auf den einfachen geschlossenen Kreislauf wird eine Differentialgleichung zweiter Ordnung erhalten, die das System beschreibt und es uns ermöglicht, den Wert von q (t) zu bestimmen..
Beispiel
Ein Induktor, ein Kondensator und ein Widerstand sind mit einer Batterie E verbunden, wie in der Figur gezeigt. Die Induktivität beträgt 2 Henry, der Kondensator 0,02 Farad und der Widerstand 16 Ohm. Zum Zeitpunkt t = 0 ist der Stromkreis geschlossen. Finden Sie die Ladung und den Strom jederzeit t> 0, wenn E = 300 Volt.
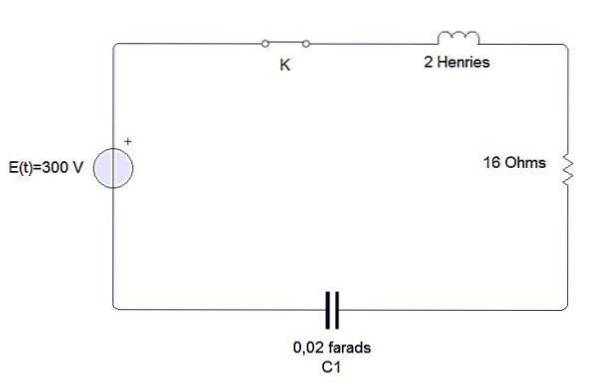
Wir haben, dass die Differentialgleichung, die diese Schaltung beschreibt, die folgende ist
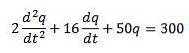
Wenn die Anfangsbedingungen q (0) = 0 sind, ist i (0) = 0 = q '(0).
Wenn wir die Laplace-Transformation anwenden, bekommen wir das
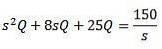
Und nach Q (t) auflösen
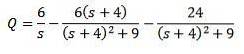
Dann wenden wir die inverse Laplace-Transformation an, die wir haben
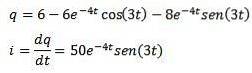
Verweise
- G. Holbrook, J. (1987). Laplace-Transformation für Elektronikingenieure. Limusa.
- Ruiz, L. M. & Hernandez, M. P. (2006). Differentialgleichungen und Laplace-Transformation mit Anwendungen. Editorial UPV.
- Simmons, G. F. (1993). Differentialgleichungen mit Anwendungen und historischen Notizen. McGraw-Hill.
- Spiegel, M. R. (1991). Laplace verwandelt sich. McGraw-Hill.
- Zill, D. G. & Cullen, M. R. (2008). Differentialgleichungen mit Randwertproblemen. Cengage Learning Editores, S.A..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.