Das mechanische Arbeit Es ist definiert als die Änderung des Energiezustands eines Systems, die durch die Einwirkung äußerer Kräfte wie Schwerkraft oder Reibung verursacht wird. Die Einheiten der mechanischen Arbeit im Internationalen System (SI) sind Newton x Meter oder Joule, abgekürzt mit J..
Mathematisch ist es als Skalarprodukt des Kraftvektors und des Verschiebungsvektors definiert. Ja F. ist die konstante Kraft und l ist die Verschiebung, beide Vektoren, die Arbeit W wird ausgedrückt als: W = F. ● l
Wenn die Kraft nicht konstant ist, müssen wir die Arbeit analysieren, die ausgeführt wird, wenn die Verschiebungen sehr klein oder unterschiedlich sind. Wenn in diesem Fall Punkt A als Startpunkt und B als Ankunftspunkt betrachtet wird, wird die Gesamtarbeit erhalten, indem alle Beiträge dazu addiert werden. Dies entspricht der Berechnung des folgenden Integrals:
Variation der Energie des Systems = Arbeit durch äußere Kräfte
ΔE = W.ext
Wenn dem System Energie hinzugefügt wird, ist W> 0 und wenn Energie W subtrahiert wird<0. Ahora bien, si ΔE = 0, puede significar que:
-Das System ist isoliert und es wirken keine äußeren Kräfte auf es.
-Es gibt externe Kräfte, aber sie arbeiten nicht am System.
Da die Energieänderung der Arbeit der äußeren Kräfte entspricht, ist die SI-Energieeinheit auch das Joule. Dies schließt jede Art von Energie ein: kinetische, potentielle, thermische, chemische und mehr..
Artikelverzeichnis
Wir haben bereits gesehen, dass Arbeit als Punktprodukt definiert ist. Nehmen wir die Definition der Arbeit, die von einer konstanten Kraft ausgeführt wird, und wenden wir das Konzept des Punktprodukts zwischen zwei Vektoren an:
W = F. ● l = F.l.cos θ
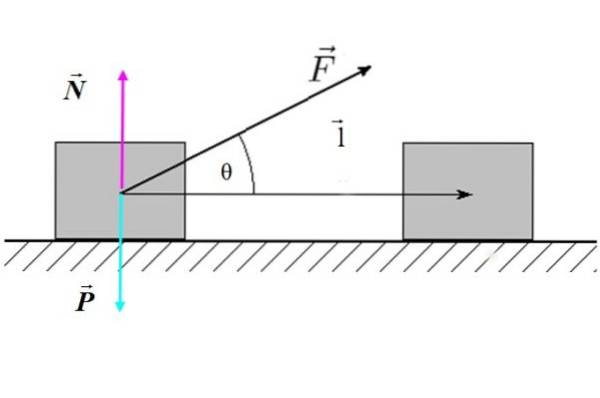
Wo F. ist die Größe der Kraft, l ist die Größe der Verschiebung und θ ist der Winkel zwischen der Kraft und der Verschiebung. In Abbildung 2 ist ein Beispiel für eine geneigte externe Kraft dargestellt, die auf einen Block (das System) wirkt und eine horizontale Verschiebung erzeugt.
Schreiben Sie die Arbeit wie folgt um:
W = (F. cos & thgr;). l
Wir können sagen, dass nur die Komponente der Kraft parallel zur Verschiebung ist: F. cos θ es in der Lage zu arbeiten. Wenn θ = 90º ist, dann ist cos θ = 0 und die Arbeit wäre Null.
Daher wird der Schluss gezogen, dass die Kräfte senkrecht zur Verschiebung keine mechanische Arbeit leisten.
Im Fall von Abbildung 2 weder die Normalkraft N. noch das Gewicht P. arbeiten, da beide senkrecht zur Verschiebung stehen l.
Wie oben erklärt, W. Es kann positiv oder negativ sein. Wenn cos θ> 0, Die Arbeit der Kraft ist positiv, da sie die gleiche Bewegungsrichtung hat.
Ja cos θ = 1, Kraft und Verschiebung sind parallel und die Arbeit ist maximal.
Im Fall cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
Wann cos θ = -1, Kraft ist der Verschiebung, wie beispielsweise der kinetischen Reibung, völlig entgegengesetzt, deren Wirkung darin besteht, das Objekt, auf das sie einwirkt, zu verlangsamen. Die Arbeit ist also minimal.
Dies stimmt mit dem überein, was zu Beginn gesagt wurde: Wenn die Arbeit positiv ist, wird dem System Energie hinzugefügt, und wenn sie negativ ist, wird sie subtrahiert.
Netzwerk W.Netz Es ist definiert als die Summe der Arbeit aller auf das System einwirkenden Kräfte:
W.Netz = ∑Wich
Dann können wir schließen, dass es zur Gewährleistung der Existenz eines mechanischen Netzes notwendig ist, dass:
-Externe Kräfte wirken auf das Objekt.
-Diese Kräfte sind nicht alle senkrecht zur Verschiebung (cos θ ≠ 0).
-Die von jeder Truppe ausgeführten Arbeiten heben sich nicht gegenseitig auf.
-Es gibt eine Verschiebung.
-Wann immer es erforderlich ist, ein Objekt aus der Ruhe in Bewegung zu setzen, ist es notwendig, mechanische Arbeiten auszuführen. Zum Beispiel einen Kühlschrank oder einen schweren Kofferraum auf eine horizontale Fläche schieben.
-Ein weiteres Beispiel für eine Situation, in der Sie mechanische Arbeiten ausführen müssen, ist das Ändern der Geschwindigkeit eines sich bewegenden Balls..
-Es ist Arbeit erforderlich, um ein Objekt auf eine bestimmte Höhe über dem Boden anzuheben.
Nun gibt es ebenso häufige Situationen, in denen nicht Die Arbeit wird erledigt, auch wenn der Schein etwas anderes anzeigt. Wir haben gesagt, um ein Objekt auf eine bestimmte Höhe zu heben, muss man arbeiten, also tragen wir das Objekt, heben es über unseren Kopf und halten es dort. Arbeiten wir??
Anscheinend ja, denn wenn das Objekt schwer ist, werden die Arme in kurzer Zeit müde, egal wie schwer es ist, aus physikalischer Sicht wird keine Arbeit geleistet. Warum nicht? Nun, weil sich das Objekt nicht bewegt.
Ein anderer Fall, in dem es trotz äußerer Kraft keine mechanische Arbeit ausführt, ist, wenn das Teilchen eine gleichmäßige Kreisbewegung aufweist.
Zum Beispiel ein Kind, das einen Stein dreht, der an eine Schnur gebunden ist. Die Saitenspannung ist die Zentripetalkraft, die es dem Stein ermöglicht, sich zu drehen. Diese Kraft ist jedoch jederzeit senkrecht zur Verschiebung. Dann führt er keine mechanischen Arbeiten aus, obwohl dies die Bewegung begünstigt.
Die kinetische Energie des Systems ist die, die es aufgrund seiner Bewegung besitzt. Ja m ist die Masse und v ist die Bewegungsgeschwindigkeit, die kinetische Energie wird mit bezeichnet K. und ist gegeben durch:
K = ½ mvzwei
Per Definition kann die kinetische Energie eines Objekts nicht negativ sein, da sowohl die Masse als auch das Quadrat der Geschwindigkeit immer positive Größen sind. Die kinetische Energie kann 0 sein, wenn sich das Objekt in Ruhe befindet.
Um die kinetische Energie eines Systems zu ändern, muss seine Geschwindigkeit variiert werden - wir werden berücksichtigen, dass die Masse konstant bleibt, obwohl dies nicht immer der Fall ist. Dies erfordert eine Netzwerkarbeit auf dem System, daher:
W.Netz = ΔK.
Dies ist der Satz der arbeitskinetischen Energie. Es sagt, dass:
Das Netzwerk entspricht der Änderung der kinetischen Energie des Systems
Es ist zu beachten, dass, obwohl K immer positiv ist, ΔK positiv oder negativ sein kann, da:
ΔK = K.Finale - K. Initiale
Ja K.Finale >K. Initiale Das System hat Energie gewonnen und ΔK> 0. Im Gegenteil, wenn K.Finale < K. Initiale, Das System hat die Stromversorgung aufgegeben.
Wenn eine Feder gedehnt (oder zusammengedrückt) wird, muss gearbeitet werden. Diese Arbeit wird im Frühjahr gespeichert, so dass diese wiederum beispielsweise an einem Block arbeiten kann, der an einem seiner Enden befestigt ist..
Das Hookesche Gesetz besagt, dass die von einer Feder ausgeübte Kraft eine Rückstellkraft ist - sie widerspricht der Verschiebung - und auch proportional zu dieser Verschiebung ist. Die Proportionalitätskonstante hängt davon ab, wie die Feder ist: weich und leicht verformbar oder starr.
Diese Kraft ist gegeben durch:
F.r = -kx
Im Ausdruck, F.r ist die Kraft, k ist die Federkonstante und x ist die Verschiebung. Das negative Vorzeichen zeigt an, dass die von der Feder ausgeübte Kraft der Verschiebung entgegenwirkt.
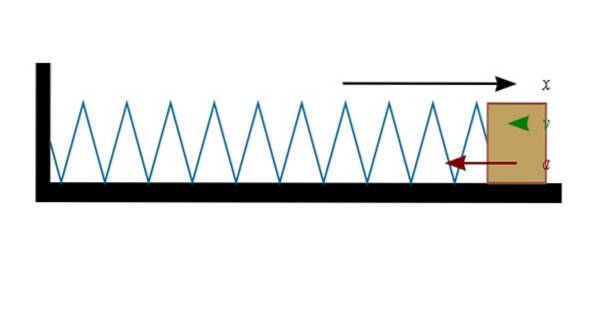
Wenn die Feder zusammengedrückt wird (in der Abbildung links), bewegt sich der Block an seinem Ende nach rechts. Und wenn die Feder gedehnt ist (nach rechts), möchte sich der Block nach links bewegen.
Um die Feder zusammenzudrücken oder zu dehnen, muss ein externer Agent die Arbeit erledigen, und da es sich um eine variable Kraft handelt, müssen wir zur Berechnung dieser Arbeit die am Anfang angegebene Definition verwenden:
Es ist sehr wichtig zu beachten, dass dies die Arbeit des externen Agenten (z. B. der Hand einer Person) ist, um die Feder zusammenzudrücken oder zu dehnen. Deshalb erscheint das negative Vorzeichen nicht. Und da die Positionen quadratisch sind, spielt es keine Rolle, ob es sich um Kompressionen oder Dehnungen handelt..
Die Arbeit, die die Feder wiederum am Block leistet, ist:
W.Frühling = -Wext
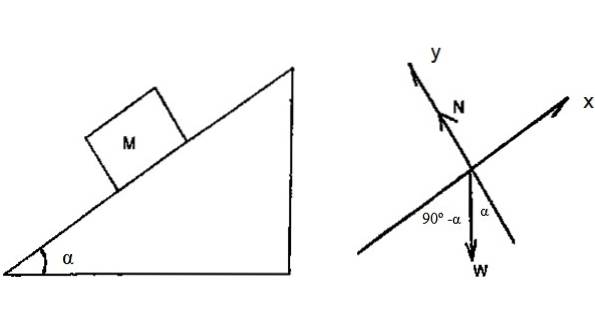
Der Block in Abbildung 4 hat eine Masse M = 2 kg und gleitet reibungslos mit α = 36,9º die schiefe Ebene hinunter. Unter der Annahme, dass es erlaubt ist, aus der Ruhe von der Oberseite der Ebene zu gleiten, deren Höhe h = 3 m beträgt, ermitteln Sie die Geschwindigkeit, mit der der Block die Basis der Ebene erreicht, unter Verwendung des Satzes der arbeitskinetischen Energie.
Das Freikörperdiagramm zeigt, dass die einzige Kraft, die am Block arbeiten kann, das Gewicht ist. Genauer gesagt: die Gewichtskomponente entlang der x-Achse.
Die vom Block in der Ebene zurückgelegte Entfernung wird mithilfe der Trigonometrie berechnet:
d = 3 / (cos 36,9º) m = 3,75 m
W.Gewicht = (Mg). d. cos (90-α) = 2 · 9,8 · 3,75 · cos 53,1 º J = 44,1 J.
Nach dem Satz der arbeitskinetischen Energie:
W.Netz = ΔK.
W.Netz = W.Gewicht
ΔK = ½ MvF.zwei- ½ Mvoderzwei
Da ist es aus der Ruhe befreit, voder = 0, So:
W.Netz = ½ MvF.zwei
Eine horizontale Feder mit einer Konstante von k = 750 N / m ist an einem Ende an einer Wand befestigt. Eine Person drückt das andere Ende um 5 cm zusammen. Berechnen Sie: a) die von der Person ausgeübte Kraft, b) die Arbeit, die sie zum Zusammendrücken der Feder geleistet hat.
a) Die Größe der von der Person ausgeübten Kraft beträgt:
F = kx = 750 N / m. 5x10 -zwei m = 37,5 N..
b) Wenn das Ende der Feder ursprünglich bei x liegt1 = 0, um von dort zur Endposition x zu gelangenzwei = 5 cm, es ist notwendig, die folgenden Arbeiten gemäß dem im vorherigen Abschnitt erhaltenen Ergebnis durchzuführen:
W.ext = ½ k (xzweizwei - x1zwei) = 0,5 x 750 x (0,05)zwei -0zwei) J = 0,9375 J..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.