Parabolische Schießeigenschaften, Formeln und Gleichungen, Beispiele

Das parabolischer Schuss Es besteht darin, ein Objekt oder Projektil in einem bestimmten Winkel zu werfen und es unter der Einwirkung der Schwerkraft bewegen zu lassen. Wenn der Luftwiderstand nicht berücksichtigt wird, folgt das Objekt unabhängig von seiner Art einem Parabelbogenpfad.

Es ist eine tägliche Bewegung, da zu den beliebtesten Sportarten solche gehören, bei denen Bälle oder Bälle entweder mit der Hand, mit dem Fuß oder mit einem Instrument wie beispielsweise einem Schläger oder einem Schläger geworfen werden.

Für seine Untersuchung wird der Parabolschuss in zwei überlagerte Bewegungen unterteilt: eine horizontale ohne Beschleunigung und die andere vertikale mit konstanter Abwärtsbeschleunigung, die Schwerkraft. Beide Bewegungen haben Anfangsgeschwindigkeit.

Angenommen, die horizontale Bewegung verläuft entlang der x-Achse und die vertikale Bewegung entlang der y-Achse. Jede dieser Bewegungen ist unabhängig von der anderen.

Da die Bestimmung der Position des Projektils das Hauptziel ist, muss ein geeignetes Referenzsystem ausgewählt werden. Details sind unten.

Artikelverzeichnis

• 1 Parabolische Schussformeln und Gleichungen
  • 1.1 - Flugbahn, maximale Höhe, maximale Zeit und horizontale Reichweite
• 2 Beispiele für parabolisches Schießen
  • 2.1 Parabolisches Schießen bei menschlichen Aktivitäten
  • 2.2 Der parabolische Schuss in der Natur
• 3 Übung
• 4 Referenzen

Parabolische Schussformeln und Gleichungen

Angenommen, das Objekt wird mit dem Winkel α in Bezug auf die Horizontal- und Anfangsgeschwindigkeit geworfen v_oder wie in der Abbildung unten links gezeigt. Der parabolische Schuss ist eine Bewegung, die im Flugzeug stattfindet xy und in diesem Fall bricht die Anfangsgeschwindigkeit wie folgt zusammen:

v_Ochse = v_oder cos α

v_Hallo = v_oder sin α

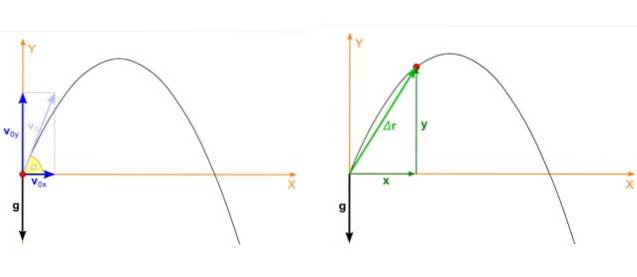
Die Position des Projektils, bei der es sich um den roten Punkt in Abbildung 2, rechtes Bild, handelt, weist ebenfalls zwei zeitabhängige Komponenten auf, eine in x und der andere in Y.. Position ist ein Vektor, der als bezeichnet wird r und seine Einheiten sind Länge.

In der Figur stimmt die Anfangsposition des Projektils mit dem Ursprung des Koordinatensystems überein, daher x_oder = 0 und_oder = 0. Dies ist nicht immer der Fall, Sie können den Ursprung überall auswählen, aber diese Auswahl vereinfacht die Berechnungen erheblich.

Die beiden Bewegungen in x und in y sind:

-x (t): ist eine gleichmäßige geradlinige Bewegung.

-y (t): entspricht einer gleichmäßig beschleunigten geradlinigen Bewegung mit g = 9,8 m / s^zwei und senkrecht nach unten zeigen.

In mathematischer Form:

x (t) = v_oder cos α.t

y (t) = v_oder .sin α.t - ½ g.t.^zwei

Der Positionsvektor ist:

r (t) = [v_oder cos α.t]ich + [v_oder .sin α.t - ½ g.t.^zwei]] j

In diesen Gleichungen wird der aufmerksame Leser feststellen, dass das Minuszeichen auf die Schwerkraft zurückzuführen ist, die auf den Boden zeigt, wobei die Richtung als negativ gewählt wird, während die Aufwärtsbewegung als positiv angenommen wird..

Da Geschwindigkeit die erste Ableitung der Position ist, leiten Sie sie einfach ab r (t) in Bezug auf die Zeit und erhalten:

v (t) = v_oder cos α ich + (v_oder .sin α - gt) j

Schließlich wird die Beschleunigung vektoriell ausgedrückt als:

zu (t) = -g j

- Flugbahn, maximale Höhe, maximale Zeit und horizontale Reichweite

Flugbahn

Um die explizite Gleichung des Pfades zu finden, bei der es sich um die Kurve y (x) handelt, müssen wir den Zeitparameter eliminieren, x (t) in der Gleichung lösen und y (t) einsetzen. Die Vereinfachung ist etwas mühsam, aber schließlich erhalten Sie:

Maximale Höhe

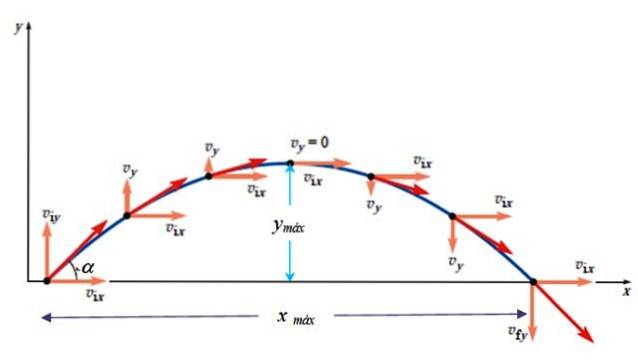
Die maximale Höhe tritt auf, wenn v_Y. = 0. Zu wissen, dass es die folgende Beziehung zwischen der Position und dem Quadrat der Geschwindigkeit gibt:

v_Y.^zwei = v_Hallo ^zwei- 2gy

Tun v_Y. = 0 gerade bei Erreichen der maximalen Höhe:

0 = v_Hallo ^zwei- 2g. Und_max → und_max = v_Hallo ^zwei/ 2 g

Mit:

v_Hallo = v_oder senα

Maximale Zeit

Die maximale Zeit ist die Zeit, die das Objekt benötigt, um und zu erreichen_max. Zur Berechnung wird verwendet:

v_Y. = v_oder .sin α - gt

Wissend, dass v_Y. wird 0 wenn t = t_max, Ergebnis:

v_oder .sin α - g.t._max = 0

t_max = v_Hallo / g

Maximale horizontale Reichweite und Flugzeit

Die Reichweite ist sehr wichtig, da sie signalisiert, wohin das Objekt fallen wird. Auf diese Weise wissen wir, ob es das Ziel trifft oder nicht. Um es zu finden, benötigen wir die Flugzeit, Gesamtzeit oder t_v.

Aus der obigen Abbildung lässt sich leicht schließen t_v = 2.t._max. Aber seien Sie vorsichtig! Dies gilt nur, wenn der Start eben ist, dh die Höhe des Startpunkts der Höhe der Ankunft entspricht. Andernfalls wird die Zeit durch Lösen der quadratischen Gleichung ermittelt, die sich aus dem Ersetzen der Endposition ergibt Y._Finale::

Y._Finale = v_oder .sin α.t_v - ½ g.t._v^zwei

In jedem Fall beträgt die maximale horizontale Reichweite:

x_max = v_Ochse. t_v

Beispiele für parabolisches Schießen

Parabolisches Schießen ist Teil der Bewegung von Menschen und Tieren. Auch von fast allen Sportarten und Spielen, bei denen die Schwerkraft interveniert. Beispielsweise:

Parabolisches Schießen bei menschlichen Aktivitäten

-Der Stein von einem Katapult geworfen.

-Der Abstoß des Torhüters.

-Der vom Werfer geworfene Ball.

-Der Pfeil, der aus dem Bogen kommt.

-Alle Arten von Sprüngen

-Wirf einen Stein mit einer Schlinge.

-Jede geworfene Waffe.

Der parabolische Schuss in der Natur

-Wasser, das aus natürlichen oder künstlichen Strahlen sprudelt, beispielsweise aus einem Brunnen.

-Steine ​​und Lava sprudeln aus einem Vulkan.

-Ein Ball, der vom Bürgersteig abprallt, oder ein Stein, der auf dem Wasser abprallt.

-Alle Arten von springenden Tieren: Kängurus, Delfine, Gazellen, Katzen, Frösche, Kaninchen oder Insekten, um nur einige zu nennen.

Übung

Eine Heuschrecke springt in einem Winkel von 55 ° zur Horizontalen und landet 0,80 Meter vor ihnen. Finden:

a) Die maximal erreichte Höhe.

b) Wenn er mit der gleichen Anfangsgeschwindigkeit springen würde, aber einen Winkel von 45º bilden würde, würde er höher gehen??

c) Was kann über die maximale horizontale Reichweite für diesen Winkel gesagt werden??

Lösung für

Wenn die vom Problem gelieferten Daten nicht die Anfangsgeschwindigkeit v enthalten_oder Die Berechnungen sind etwas mühsamer, aber aus den bekannten Gleichungen kann ein neuer Ausdruck abgeleitet werden. Ab:

x_max = v_Ochse . t_Flug = v_oder.cos α. t_v

Wenn es später landet, kehrt die Höhe auf 0 zurück, also:

v_oder .sin α.t_v - ½ g.t._v^zwei= 0

Was t_v ist ein gemeinsamer Faktor, es ist vereinfacht:

v_oder .sin α - ½ g.t._v= 0

Wir können t löschen_v aus der ersten Gleichung:

t_v = x_max / v_oder.cos α

Und im zweiten ersetzen:

v_oder .sin α - (½ g.x._max / v_oder.cos α) = 0

Durch Multiplikation aller Begriffe mit v_oder.cos αDer Ausdruck wird nicht geändert und der Nenner verschwindet:

(v_oder .sin α.) (v_oder.cos α) - ½ g.x._max = 0

v_oder^zwei sin α. cos α = ½ g.x._max

Es kann bereits gelöscht werden v_oder oder ersetzen Sie auch die folgende Identität:

sin 2α = 2 sin α. cos α → v_oder^zwei sin 2α = g.x._max

Ist berechnet v_oder^zwei::

v_oder^zwei = g.x_max /. sin 2α = (9,8 · 0,8 / sin 110) m^zwei/ s^zwei = 8,34 m^zwei/ s^zwei

Und schließlich die maximale Höhe:

Y._max= v_Hallo ^zwei/ 2g = (8,34 x sin^zwei 55) / (2 × 9,8) m = 0,286 m = 28,6 cm

Lösung b

Der Hummer schafft es, die gleiche horizontale Geschwindigkeit beizubehalten, aber durch Verringern des Winkels:

Y._max= v_Hallo ^zwei/ 2g = (8,34 x sin^zwei 45) / (2 × 9,8) m = 0,213 m = 21,3 cm

Erreicht eine niedrigere Höhe.

Lösung c

Die maximale horizontale Reichweite beträgt:

x_max = v_oder^zwei sen 2nd / G

Durch Variieren des Winkels ändert sich auch die horizontale Reichweite:

x_max = 8,34 sen 90 / 9.8  m = 0,851 m = 85,1 cm

Der Sprung ist jetzt länger. Der Leser kann überprüfen, ob es für den 45 ° -Winkel maximal ist, weil:

sin 2α = sin 90 = 1.

Verweise

1. Figueroa, D. 2005. Reihe: Physik für Naturwissenschaften und Technik. Band 1. Kinematik. Herausgegeben von Douglas Figueroa (USB).
2. Giambattista, A. 2010. Physik. Zweite Ausgabe. Mcgraw Hügel.
3. Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
4. Resnick, R. 1999. Physics. Vol. 1. 3rd Ed. In Spanisch. Compañía Editorial Continental S.A. von C.V..
5. Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1.