
Erklärung des Überlagerungssatzes, Anwendungen, gelöste Übungen
Das Überlagerungssatz, In elektrischen Schaltkreisen wird festgestellt, dass die Spannung zwischen zwei Punkten oder der Strom durch sie die algebraische Summe der Spannungen (oder Ströme, falls dies der Fall ist) aufgrund jeder Quelle ist, als ob jeder auf unterschiedliche Weise wirkt Unabhängig.
Dieser Satz ermöglicht es uns, lineare Schaltkreise zu analysieren, die mehr als eine unabhängige Quelle enthalten, da nur der Beitrag jeder einzelnen separat berechnet werden muss..

Die lineare Abhängigkeit ist entscheidend für die Anwendung des Satzes. Eine lineare Schaltung ist eine Schaltung, deren Antwort direkt proportional zum Eingang ist.
Zum Beispiel besagt das Ohmsche Gesetz, das auf einen elektrischen Widerstand angewendet wird, dass V = i.R., wo V. ist die Spannung, R. ist der Widerstand e ich ist der Strom. Es ist dann eine lineare Abhängigkeit von Spannung und Strom in einem Widerstand.
In linearen Schaltungen wird das Überlagerungsprinzip unter Berücksichtigung der folgenden Punkte angewendet:
-Jede unabhängige Spannungsquelle muss separat betrachtet werden und dazu müssen alle anderen ausgeschaltet werden. Es reicht aus, alle nicht analysierten Werte auf 0 V zu setzen oder sie im Schema durch einen Kurzschluss zu ersetzen.
-Wenn die Quelle Strom ist, müssen Sie den Stromkreis öffnen.
-Wenn der Innenwiderstand von Strom- und Spannungsquellen berücksichtigt wird, müssen diese an Ort und Stelle bleiben und Teil des restlichen Stromkreises sein..
-Wenn es abhängige Quellen gibt, müssen diese so bleiben, wie sie in der Schaltung erscheinen.
Artikelverzeichnis
- 1 Anwendungen
- 2 Schritte zum Anwenden des Überlagerungssatzes
- 3 Gelöste Übungen
- 3.1 - Beispiel 1
- 3.2 - Übung 2
- 4 Referenzen
Anwendungen
Der Überlagerungssatz wird verwendet, um einfachere und leichter zu handhabende Schaltungen zu erhalten. Es sollte jedoch immer bedacht werden, dass dies, wie eingangs erwähnt, nur für Personen mit linearen Antworten gilt.
So kann es beispielsweise nicht direkt zur Leistungsberechnung verwendet werden, da die Leistung mit dem Strom in Beziehung steht durch:
P = izwei R.
Da der Strom quadratisch ist, ist die Antwort nicht linear. Sie gilt auch nicht für Magnetkreise mit Transformatoren..
Andererseits bietet der Überlagerungssatz die Möglichkeit, die Auswirkung jeder Quelle auf die Schaltung zu kennen. Und natürlich ist es durch seine Anwendung möglich, es vollständig zu lösen, dh Ströme und Spannungen durch jeden Widerstand zu kennen.
Der Überlagerungssatz kann auch in Verbindung mit anderen Schaltungssätzen, beispielsweise dem von Thévenin, verwendet werden, um komplexere Konfigurationen zu lösen..
In Wechselstromkreisen ist der Satz ebenfalls nützlich. In diesem Fall arbeiten wir mit Impedanzen anstelle von Widerständen, solange der Gesamtgang jeder Frequenz unabhängig berechnet werden kann..
Schließlich ist in elektronischen Systemen der Satz sowohl für die Gleichstrom- als auch für die Wechselstromanalyse getrennt anwendbar.
Schritte zum Anwenden des Überlagerungssatzes
-Deaktivieren Sie alle unabhängigen Quellen gemäß den Anweisungen zu Beginn, mit Ausnahme der zu analysierenden.
-Bestimmen Sie den Ausgang, entweder Spannung oder Strom, den diese einzelne Quelle erzeugt.
-Wiederholen Sie die beiden für alle anderen Quellen beschriebenen Schritte.
-Berechnen Sie die algebraische Summe aller Beiträge, die in den vorherigen Schritten gefunden wurden.
Gelöste Übungen
Die folgenden Arbeitsbeispiele verdeutlichen die Verwendung des Theorems in einigen einfachen Schaltungen.
- Beispiel 1
Ermitteln Sie in der in der folgenden Abbildung gezeigten Schaltung den Strom durch jeden Widerstand mithilfe des Überlagerungssatzes.
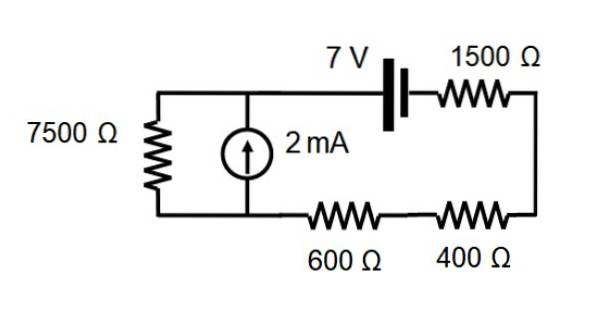
Lösung
Beitrag der Spannungsquelle
Zunächst wird die Stromquelle eliminiert, wodurch die Schaltung folgendermaßen aussieht:

Der äquivalente Widerstand wird durch Addition des Wertes jedes Widerstands ermittelt, da alle in Reihe geschaltet sind:
7500 +600 +400 + 1500 Ω = 10.000 Ω
Anwendung des Ohmschen Gesetzes V = I.R. und Löschen des Stroms:
I = V / R = 7 / 10.000 A = 0,0007 A = 0,7 mA
Dieser Strom ist für alle Widerstände gleich.
Beitrag der aktuellen Quelle
Die Spannungsquelle wird sofort eliminiert, um nur mit der Stromquelle zu arbeiten. Die resultierende Schaltung ist unten gezeigt:
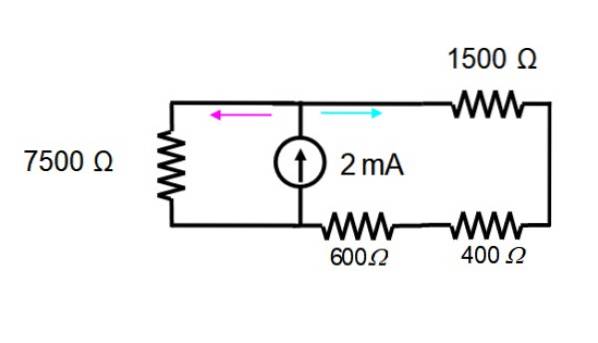
Die Widerstände auf dem Bildschirm rechts sind in Reihe geschaltet und können durch einen einzigen ersetzt werden:
600 + 400 + 1500 Ω = 2500 Ω
Die resultierende Schaltung sieht folgendermaßen aus:
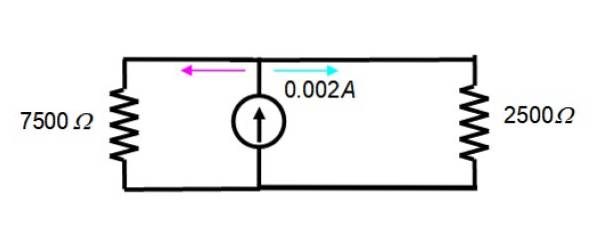
Der Strom von 2 mA = 0,002 A wird zwischen den beiden Widerständen in der Figur aufgeteilt, daher gilt die Gleichung des Stromteilers:
ichx = (R.Gl/ R.x) ICHT.
Wo ichx ist der Strom im Widerstand R.x, R.Gl symbolisiert den äquivalenten Widerstand e ichT. ist der Gesamtstrom. Es ist notwendig, den äquivalenten Widerstand zwischen beiden zu finden, in dem Wissen, dass:
1 / R.Gl = (1 / R.1) + (1 / R.zwei)
Deshalb:
1 / R.Gl = (1/7500) + (1/2500) = 1/1875 → R.Gl = 1875 Ω
Für diese andere Schaltung wird der Strom durch den 7500 Ω-Widerstand durch Einsetzen von Werten in die Stromteilergleichung ermittelt:
ich7500 Ω = (1875/7500). 0,002 A = 0,0005 A = 0,5 mA
Während derjenige, der durch den 2500 Ω Widerstand geht, ist:
ich2500 Ω = 2 mA - 0,5 mA = 1,5 mA
Anwendung des Überlagerungssatzes
Nun wird der Überlagerungssatz für jeden Widerstand angewendet, beginnend mit 400 Ω:
ich400 Ω = 1,5 mA - 0,7 mA = 0,8 mA
Wichtig: für diesen Widerstand, Die Ströme werden abgezogen, wie sie in der entgegengesetzten Richtung zirkulieren, nach sorgfältiger Beobachtung der Figuren, in denen die Richtungen der Ströme unterschiedliche Farben haben.
Der gleiche Strom fließt gleichermaßen durch die 1500 Ω- und 600 Ω-Widerstände, da sie alle in Reihe geschaltet sind.
Der Satz wird dann angewendet, um den Strom durch den 7500 Ω-Widerstand zu ermitteln:
ich7500 Ω = 0,7 mA + 0,5 mA = 1,2 mA
Wichtig: Beachten Sie beim 7500 Ω-Widerstand Folgendes Die Ströme summieren sich, denn in beiden Kreisläufen zirkulieren sie beim Durchgang durch diesen Widerstand in die gleiche Richtung. Auch hier ist es notwendig, die Richtungen der Ströme sorgfältig zu beobachten.
- Übung 2
Ermitteln des Stroms und der Spannung am 12 Ω-Widerstand mithilfe des Überlagerungssatzes.
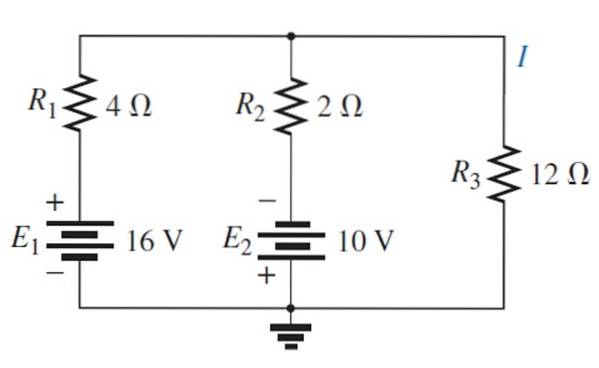
Lösung
Schriftart E wird ersetzt1 mit einem Kurzschluss:
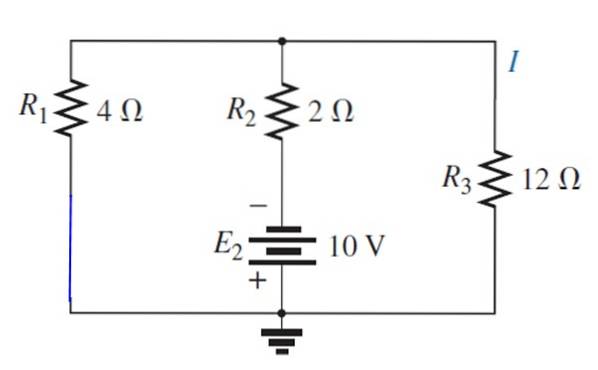
Die resultierende Schaltung wird wie folgt gezeichnet, um die parallel verbleibenden Widerstände leicht sichtbar zu machen:
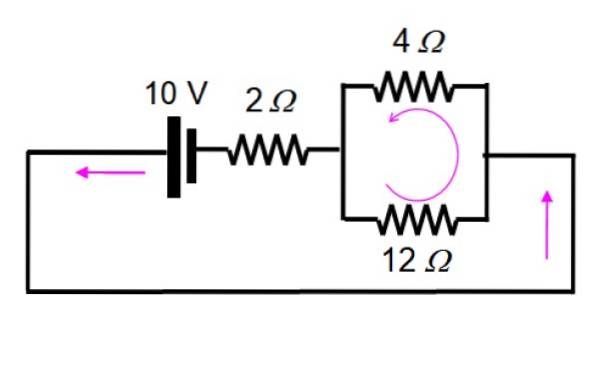
Und jetzt wird es durch Anwenden von Serien und Parallelen gelöst:
1 / R.Gl = (1/12) + (1/4) = 1/3 → R.Gl = 3 Ω
Dieser Widerstand ist wiederum in Reihe mit dem von 2 Ω, daher ist der Gesamtwiderstand 5 Ω. Der Gesamtstrom beträgt:
I = V / R = 10 V / 5 Ω = 2 A.
Dieser Stream ist unterteilt in:
ich12Ω = (3/12) 2 A = 0,5 A.
Daher ist die Spannung:
V.12Ω = 0,5 A × 12 Ω = 6 V.
Jetzt ist Quelle E aktiviert1::
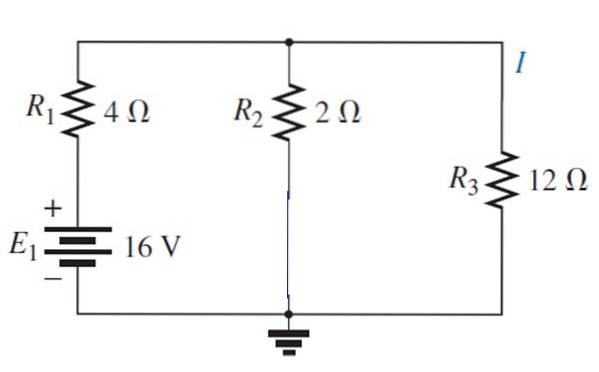
Die resultierende Schaltung kann wie folgt gezeichnet werden:

1 / R.Gl = (1/12) + (1/2) = 7/12 → R.Gl = 12/7 Ω
Und in Serie mit dem von 4 Ω es ergibt sich ein äquivalenter Widerstand 40/7 Ω. In diesem Fall beträgt der Gesamtstrom:
I = V / R = 16 V / (40/7) Ω = 14/5 A.
Der Spannungsteiler wird erneut mit folgenden Werten angelegt:
ich12Ω = ((12/7) / 12) (14/5) A = 0,4 A.
Der resultierende Strom ist: 0,5 - 0,4 A = 0,1 A.. Beachten Sie, dass sie subtrahiert wurden, da der Strom von jeder Quelle einen anderen Sinn hat, wie in der ursprünglichen Schaltung zu sehen ist.
Die Spannung am Widerstand beträgt:
V.12Ω = 0,4 A × 12 Ω = 4,8 V.
Schließlich beträgt die Gesamtspannung: 6 V - 4,8 V = 1,2 V.
Verweise
- Alexander, C. 2006. Grundlagen elektrischer Schaltungen. 3 .. Auflage. Mc Graw Hill.
- Boylestad, R. 2011. Einführung in die Schaltungsanalyse. 2 .. Auflage. Pearson.
- Dorf, R. 2006. Einführung in elektrische Schaltungen. 7 .. Auflage. John Wiley & Sons.
- Edminister, J. 1996. Electrical Circuits. Schaum-Serie. 3 .. Auflage. Mc Graw Hill
- Wikipedia. Aktueller Teiler. Wiederhergestellt von: es.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.