
Nortons Satzbeschreibung, Anwendungen, Beispiele und Übungen
Das Nortons Theorem, Die Anwendung auf elektrische Schaltkreise stellt fest, dass ein linearer Schaltkreis mit zwei Anschlüssen a und b durch einen vollständig äquivalenten ersetzt werden kann, der aus einer Stromquelle namens I bestehtNicht parallel geschaltet mit einem Widerstand R.Nicht.
Sagte Strom ichNicht Ich hörteN. Es ist dasjenige, das zwischen den Punkten a und b fließen würde, wenn sie kurzgeschlossen würden. Der Widerstand R.N. ist der äquivalente Widerstand zwischen den Klemmen, wenn alle unabhängigen Quellen ausgeschaltet sind. Alles, was gesagt wird, ist in Abbildung 1 dargestellt.

Das schwarze Kästchen in der Abbildung enthält die lineare Schaltung, die durch das Norton-Äquivalent ersetzt werden soll. Eine lineare Schaltung ist eine Schaltung, bei der der Eingang und der Ausgang eine lineare Abhängigkeit haben, wie beispielsweise die Beziehung zwischen der Spannung V und dem Gleichstrom I in einem ohmschen Element: V = I.R..
Dieser Ausdruck entspricht dem Ohmschen Gesetz, wobei R der Widerstand ist, der auch eine Impedanz sein kann, wenn es sich um einen Wechselstromkreis handelt.
Nortons Theorem wurde vom Elektrotechniker und Erfinder Edward L. Norton (1898-1983) entwickelt, der lange Zeit für Bell Labs arbeitete..
Artikelverzeichnis
- 1 Anwendungen des Norton-Theorems
- 1.1 Beziehung zwischen den Theoremen von Norton und Thevenin
- 2 Beispiel
- 3 Übung gelöst
- 4 Referenzen
Anwendungen des Norton-Theorems
Wenn Sie sehr komplizierte Netzwerke mit vielen Widerständen oder Impedanzen haben und die Spannung zwischen diesen oder den durch sie fließenden Strom berechnen möchten, vereinfacht der Satz von Norton die Berechnungen, da das Netzwerk, wie wir gesehen haben, durch ersetzt werden kann eine kleinere und handlichere Schaltung.
Auf diese Weise ist der Satz von Norton sehr wichtig, wenn Schaltungen mit mehreren Elementen entworfen und ihre Reaktion untersucht werden..
Beziehung zwischen Norton- und Thevenin-Theoremen
Nortons Theorem ist das Duale von Thevenins Theorem, was bedeutet, dass sie äquivalent sind. Der Satz von Thevenin zeigt, dass die Black Box in Abbildung 1 durch eine Spannungsquelle in Reihe mit einem Widerstand ersetzt werden kann, der als Thevenin-Widerstand R bezeichnet wirdTh. Dies wird in der folgenden Abbildung ausgedrückt:
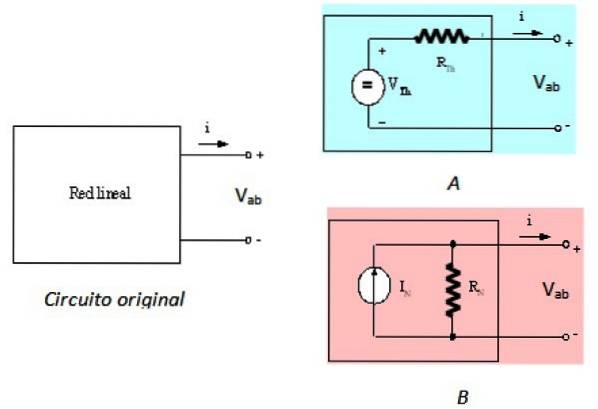
Die Schaltung links ist die ursprüngliche Schaltung, das lineare Netzwerk in der Black Box, die Schaltung A oben rechts ist das Thevenin-Äquivalent und die Schaltung B. Es ist das Norton-Äquivalent, wie beschrieben. Von den Klemmen a und b aus gesehen sind die drei Schaltkreise äquivalent.
Beachten Sie nun Folgendes:
-In der ursprünglichen Schaltung beträgt die Spannung zwischen den Klemmen V.ab.
-V.ab = V.Th in der Schaltung ZU
-Schließlich V.ab = IchN..R.N. in der Schaltung B.
Wenn die Klemmen a und b in allen drei Stromkreisen kurzgeschlossen sind, muss sichergestellt sein, dass die Spannung und der Strom zwischen diesen Punkten für alle drei gleich sind, da sie gleich sind. Dann:
-In der ursprünglichen Schaltung ist der Strom i.
-Für die Schaltung A ist der Strom i = V.Th / R.Th, nach dem Ohmschen Gesetz.
-Schließlich ist in Schaltung B der Strom I.N.
Daher wird der Schluss gezogen, dass die Widerstände von Norton und Thevenin den gleichen Wert haben und dass der Strom gegeben ist durch:
i = ichN. = V.Th / R.Th = V.Th / R.N.
Beispiel
Um den Satz von Norton korrekt anzuwenden, werden die folgenden Schritte ausgeführt:
-Isolieren Sie vom Netzwerk den Abschnitt der Schaltung, für den das Norton-Äquivalent gefunden werden soll.
-Geben Sie im verbleibenden Stromkreis die Klemmen a und b an.
-Ersetzen Sie die Spannungsquellen durch Kurzschlüsse und die Stromquellen durch offene Stromkreise, um den äquivalenten Widerstand zwischen den Klemmen a und b zu ermitteln. Das ist R.N..
-Bringen Sie alle Quellen wieder in ihre ursprüngliche Position, schließen Sie die Klemmen a und b kurz und suchen Sie den Strom, der zwischen ihnen fließt. Das bin ichN..
-Zeichnen Sie das Norton-Ersatzschaltbild gemäß den Angaben in Abbildung 1. Sowohl die Stromquelle als auch der Ersatzwiderstand sind parallel.
Sie können auch den Satz von Thevenin anwenden, um R zu findenTh, dass wir bereits wissen, ist gleich R.N., dann kannst du mich nach Ohmschem Gesetz findenN. und fahren Sie mit dem Zeichnen der resultierenden Schaltung fort.
Und jetzt sehen wir uns ein Beispiel an:
Finden Sie das Norton-Äquivalent zwischen den Punkten A und B der folgenden Schaltung:
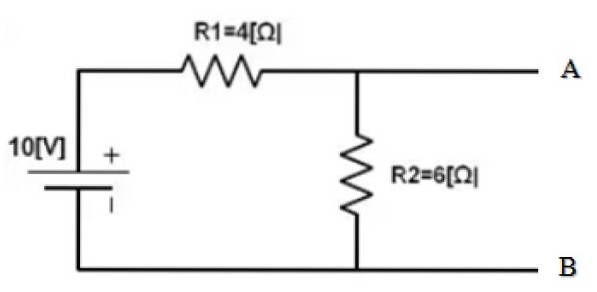
Der Teil der Schaltung, dessen Äquivalent zu finden ist, ist bereits isoliert. Und die Punkte A und B sind klar bestimmt. Das Folgende dient zum Kurzschließen der 10-V-Quelle und zum Ermitteln des äquivalenten Widerstands des erhaltenen Stromkreises:
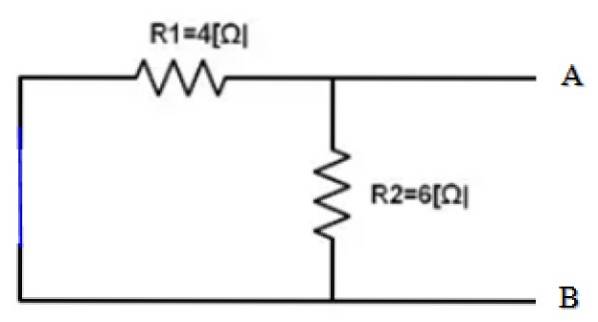
Ansichten von den Terminals A und B., beide Widerstände R.1 und R.zwei sind daher parallel:
1 / R.Gl = 1 / R.12 = (1/4) + (1/6) Ω-1 = 5/12 Ω-1 → R.Gl = 12/5 Ω = 2,4 Ω
Dann wird die Quelle an ihren Platz zurückgebracht und die Punkte A und B werden kurzgeschlossen, um den Strom zu finden, der dort zirkuliert. Dies ist I.N.. In diesem Fall:
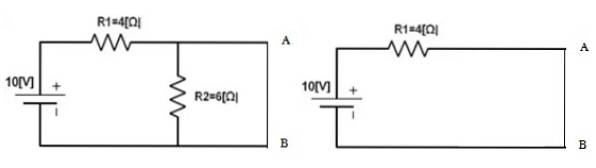
ichN. = 10 V / 4 Ω = 2,5 A.
Norton-Äquivalent
Schließlich wird das Norton-Äquivalent mit den gefundenen Werten gezeichnet:
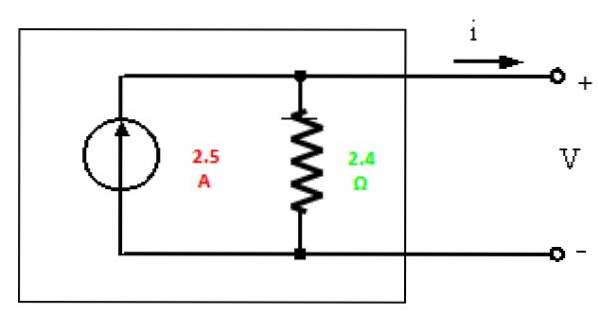
Übung gelöst
In der Schaltung der folgenden Abbildung:
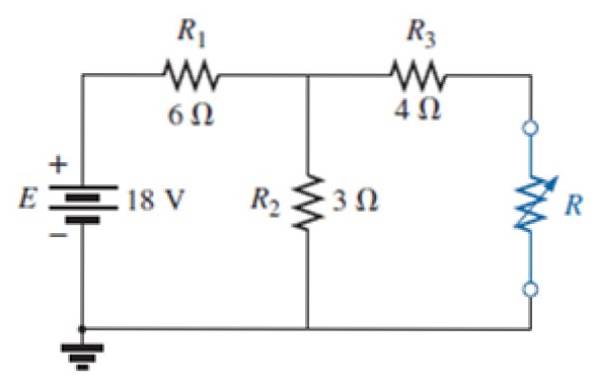
a) Finden Sie das Norton-Ersatzschaltbild des externen Netzwerks zum blauen Widerstand.
b) Finden Sie auch das Thévenin-Äquivalent.
Lösung für
Befolgen Sie die oben angegebenen Schritte, um die Quelle kurzzuschließen:
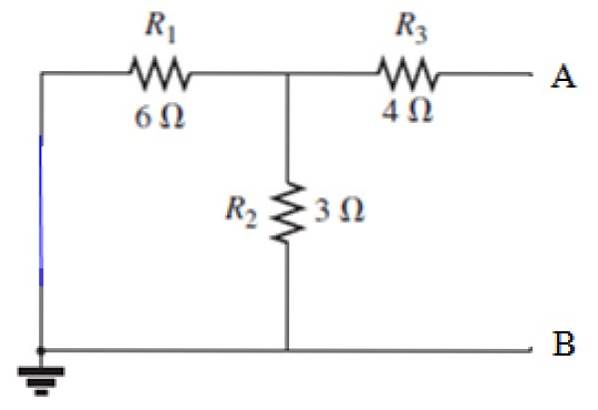
Berechnung von RN
Blick von den Klemmen A und B, Widerstand R.3 liegt in Reihe mit der durch Widerstände R gebildeten Parallele1 und R.zwei, Berechnen wir zunächst den äquivalenten Widerstand dieser Parallele:
1 / R.12 = (1/6) + (1/3) Ω-1 = 1/2 Ω-1 → R.Gl = 2/1 Ω = 2Ω
Und dann ist diese Parallele in Reihe mit R.3, so dass der äquivalente Widerstand ist:
R.Gl = 2 Ω + 4 Ω = 6 Ω
Dies ist der Wert von beiden R.N. ab R.Th, wie zuvor erklärt.
IN Berechnung
Die Klemmen A und B werden dann kurzgeschlossen und bringen die Quelle an ihren Platz zurück:
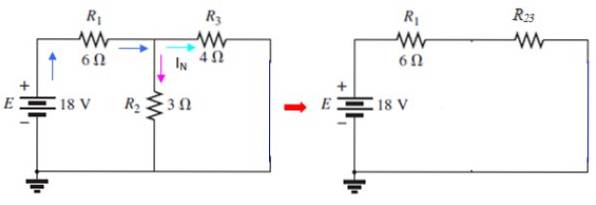
Der Strom durch ich3 ist das aktuelle ichN. gesucht, die mit der Mesh-Methode oder mit Serien und Parallel bestimmt werden kann. In dieser Schaltung R.zwei und R.3 sind parallel:
1 / R.2. 3 = (1/3) + (1/4) Ω-1 = 7/12 Ω-1 → R.2. 3 = 12/7 Ω
Der Widerstand R.1 ist in Reihe mit dieser Parallele, dann:
R.123 = 6 + (12/7) Ω = 54/7 Ω
Der aus der Quelle austretende Strom (blaue Farbe) wird nach dem Ohmschen Gesetz berechnet:
V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 A.
Dieser Strom ist in zwei Teile unterteilt: einen, der durch R fließtzwei und eine andere, die R kreuzt3. Der Strom durch paralleles R.2. 3 es ist dasselbe, das durch R geht1, wie in der Zwischenschaltung in der Figur zu sehen. Die Spannung dort ist:
V.2. 3 = I.R.2. 3 = (7/3) A. (12/7) Ω = 4 V.
Beide Widerstände R.zwei und R.3 sind bei dieser Spannung, da sie parallel sind, daher:
ich3 = V.2. 3 / R.3 = 4 V / 4 Ω = 1 A.
Wir haben bereits nach dem Norton-Strom gesucht, da ich wie gesagt schon gesagt habe3 = IchN., dann:
ichN. = 1 A.
Norton-Äquivalent
Alles ist bereit, das Norton-Äquivalent dieser Schaltung zwischen den Punkten A und B zu zeichnen:
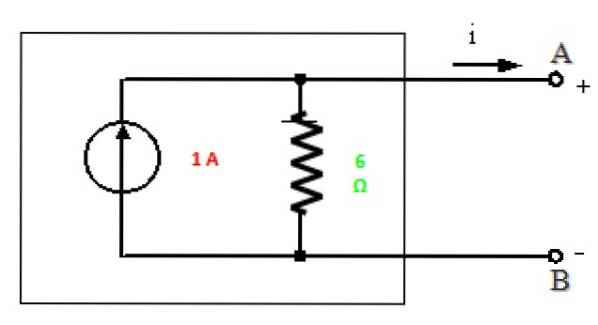
Lösung b
Das Thévenin-Äquivalent zu finden ist sehr einfach, da R.Th = R.N.= 6 Ω und wie in den vorhergehenden Abschnitten erläutert:
V.Th = IchN.. R.N. = 1 A. 6 Ω = 6 V.
Das Thévenin-Ersatzschaltbild lautet:
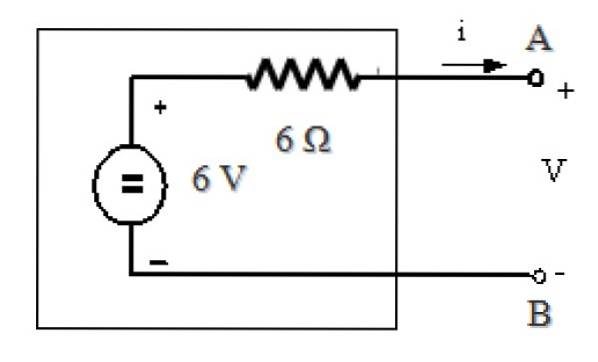
Verweise
- Alexander, C. 2006. Grundlagen elektrischer Schaltungen. 3 .. Auflage. Mc Graw Hill.
- Boylestad, R. 2011. Einführung in die Schaltungsanalyse. 2 .. Auflage. Pearson.
- Dorf, R. 2006. Einführung in elektrische Schaltungen. 7 .. Auflage. John Wiley & Sons.
- Edminister, J. 1996. Electrical Circuits. Schaum-Serie. 3 .. Auflage. Mc Graw Hill.
- Wikipedia. Nortons Theorem. Wiederhergestellt von: es.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.