
Satz, Beweis, Anwendungen und Übungen von Green
Das Satz von Green ist eine Berechnungsmethode, mit der Linienintegrale mit Doppelflächen- oder Oberflächenintegralen in Beziehung gesetzt werden. Die beteiligten Funktionen müssen als Vektorfelder bezeichnet und im Pfad C definiert werden.
Beispielsweise kann es sehr schwierig sein, einen Linienintegralausdruck zu lösen. Durch die Implementierung des Greenschen Theorems werden Doppelintegrale jedoch ziemlich grundlegend. Es ist immer wichtig, die positive Richtung der Flugbahn zu beachten, dies bezieht sich auf die Richtung gegen den Uhrzeigersinn.

Der Satz von Green ist ein besonderer Fall des Satzes von Stokes, bei dem die Projektion der Vektorfunktion in der xy-Ebene durchgeführt wird.
Artikelverzeichnis
- 1 Definition
- 2 Demo
- 3 Anwendungen
- 4 Geschichte
- 5 Beziehung zu anderen Theoremen
- 6 Übungen
- 7 Referenzen
Definition
Der Ausdruck des Satzes von Green lautet wie folgt:
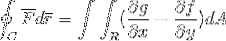
Der erste Term zeigt das durch den Pfad "C" definierte Linienintegral des Skalarprodukts zwischen der Vektorfunktion "F" und dem des Vektors "r"..
C: Dies ist der definierte Pfad, auf den die Vektorfunktion projiziert wird, solange sie für diese Ebene definiert ist.
F: Vektorfunktion, bei der jede ihrer Komponenten durch eine solche Funktion definiert ist (f, g).
r: Es ist ein Vektor, der den Bereich R tangiert, über den das Integral definiert ist. In diesem Fall arbeiten wir mit einem Differential dieses Vektors.
Im zweiten Term sehen wir den Satz von Green entwickelt, in dem das im Bereich R der Differenz der partiellen Ableitungen von g und f definierte Doppelintegral in Bezug auf x bzw. y beobachtet wird. Durch ein Flächendifferential, das nichts anderes als das Produkt beider zweidimensionaler Differentiale ist (dx.dy).
Dieser Satz ist perfekt für Raum- und Oberflächenintegrale anwendbar.
Demonstration
Um den Satz von Green auf einfache Weise zu beweisen, wird diese Aufgabe in zwei Teile unterteilt. Zunächst nehmen wir an, dass die Vektorfunktion F nur im Versor definiert ist ich. Während die Funktion "g" dem Versor entspricht j wird gleich Null sein.
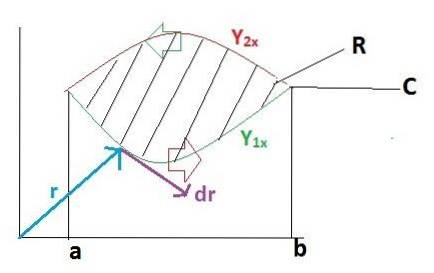
F = f (x, y)ich + g (x, y)j = f (x, y)ich + 0
r = xich + Y.j
dr = dxich + dyj
Zuerst entwickeln wir das Linienintegral über der Trajektorie C, für die die Trajektorie in zwei Abschnitte unterteilt wurde, die zuerst von a nach b und dann von b nach a verlaufen.
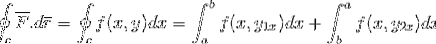
Die Definition des Grundsatzes der Analysis wird für ein bestimmtes Integral angewendet.
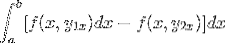
Der Ausdruck wird in ein einzelnes Integral umgeordnet, das Negative wird zu einem gemeinsamen Faktor und die Reihenfolge der Faktoren wird umgekehrt.
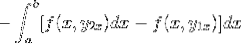
Wenn wir diesen Ausdruck im Detail betrachten, wird deutlich, dass wir uns bei Anwendung der primitiven Funktionskriterien in Gegenwart des Integrals des Ausdrucks befinden, das von f in Bezug auf y abgeleitet ist. In Parametern ausgewertet
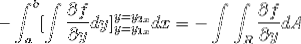
Nun genügt die Annahme, dass die Vektorfunktion F nur für g (x, y) definiert ist.j. Wenn auf ähnliche Weise wie im vorherigen Fall gearbeitet wird, wird Folgendes erhalten:
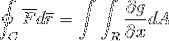
Zum Abschluss werden die 2 Proofs genommen und zusammengefügt, falls die Vektorfunktion Werte für beide Versoren annimmt. Auf diese Weise wird gezeigt, wie das Linienintegral nach seiner Definition und Betrachtung als eindimensionale Trajektorie für die Ebene und den Raum vollständig entwickelt werden kann.
F = f (x, y)ich + g (x, y)j
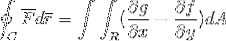
Auf diese Weise wird der Satz von Green bewiesen.
Anwendungen
Die Anwendungen des Satzes von Green sind in den Bereichen Physik und Mathematik breit gefächert. Diese erstrecken sich auf jede Anwendung oder Verwendung, die für die Linienintegration verwendet werden kann.
Die mechanische Arbeit, die eine Kraft F durch einen Pfad C leistet, kann durch ein Linienintegral entwickelt werden, das mit Hilfe des Greenschen Theorems als Doppelintegral einer Fläche ausgedrückt wird.
Die Trägheitsmomente vieler Körper, die an verschiedenen Anwendungspunkten äußeren Kräften ausgesetzt sind, reagieren auch auf Linienintegrale, die mit dem Satz von Green entwickelt werden können..
Dies hat mehrere Funktionen bei den Widerstandsstudien von verwendeten Materialien. Wo externe Werte vor der Ausarbeitung verschiedener Elemente quantifiziert und berücksichtigt werden können.
Im Allgemeinen erleichtert der Satz von Green das Verständnis und die Definition der Bereiche, in denen Vektorfunktionen in Bezug auf eine Region gemäß einer Trajektorie definiert sind.
Geschichte
Es wurde 1828 in der Arbeit veröffentlicht Mathematische Analyse der Theorien von Elektrizität und Magnetismus, geschrieben von dem britischen Mathematiker George Green. Darin werden ganz entscheidende Abschnitte in der Anwendung des Kalküls in der Physik untersucht, wie das Konzept möglicher Funktionen, die Funktionen von Green und die Anwendung seines selbstbetitelten Theorems.
George Green formalisierte seine Studentenkarriere im Alter von 40 Jahren und war bis jetzt ein völlig autodidaktischer Mathematiker. Nach seinem Studium an der Universität von Cambridge setzte er seine Forschung fort und leistete Beiträge zu Akustik, Optik und Hydrodynamik, die bis heute gültig sind..
Beziehung zu anderen Theoremen
Der Satz von Green ist ein Sonderfall und ergibt sich aus zwei anderen sehr wichtigen Sätzen auf dem Gebiet der Analysis. Dies sind der Kelvin-Stokes-Satz und der Divergenzsatz oder Gauss Ostrogradski.
Ausgehend von einem der beiden Sätze ist es möglich, zum Satz von Green zu gelangen. Bestimmte Definitionen und Sätze sind notwendig, um solche Beweise zu entwickeln..
Ausbildung
- Die folgende Übung zeigt, wie ein Linienintegral in Bezug auf einen Bereich R in ein Doppelintegral umgewandelt wird.
Der ursprüngliche Ausdruck lautet wie folgt:
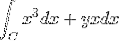
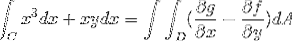
Von wo werden die Funktionen genommen, die f und g entsprechen
f (x, y) = x3 g (x, y) = yx
df / dy = 0 dg / dx = y
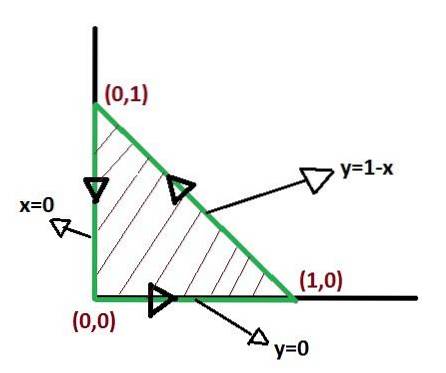
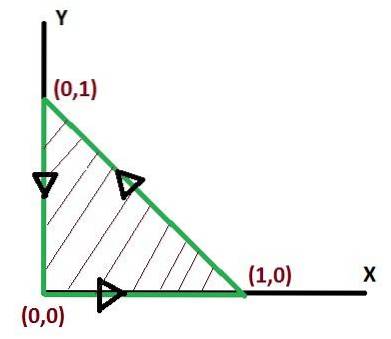
Es gibt keine einzige Möglichkeit, die Grenzen der Integration zu definieren, wenn der Satz von Green angewendet wird. Es gibt jedoch Möglichkeiten, wie die Integrale nach der Definition einfacher sein können. Die Optimierung der Integrationsgrenzen verdient daher Beachtung.
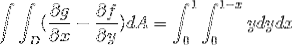
Wo erhalten wir beim Lösen der Integrale:
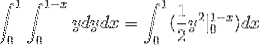
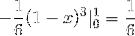
Dieser Wert entspricht in kubischen Einheiten dem Bereich unterhalb der Vektorfunktion und über dem durch C definierten dreieckigen Bereich.
Für den Fall des Linienintegrals ohne Durchführung der Greenschen Methode wäre es notwendig gewesen, die Funktionen in jedem Abschnitt der Region zu parametrisieren. Führen Sie also 3 parametrisierte Integrale für die Auflösung aus. Dies ist ein ausreichender Beweis für die Wirksamkeit, die Robert Green mit seinem Theorem in die Analysis eingebracht hat.
Verweise
- Einführung in die Kontinuumsmechanik. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23. Juli. 2009
- Multivariable Infinitesimalrechnung. James Stewart. Cengage Learning, 22. März 2011
- Eine informelle Geschichte des Satzes von Green und der damit verbundenen Ideen. James Joseph Cross. Institut für Mathematik, Universität Melbourne, 1975
- Wärmeleitung mit Greens-Funktionen. Kevin D. Cole, James V. Beck, A. Haji-Scheich, Bahman Litkouhi. Taylor & Francis, 16. Juli 2010
- Anwendung des Greenschen Theorems auf die Extremisierung linearer Integrale. Technisches Verteidigungsinformationszentrum, 1961


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.