
Theorie charakteristischer Mengen, Elemente, Beispiele, Übungen
Das Mengenlehre Es ist ein Zweig der Logik-Mathematik, der für die Untersuchung der Beziehungen zwischen Entitäten verantwortlich ist, die als Mengen bezeichnet werden. Die Sets zeichnen sich durch Sammlungen von Objekten gleicher Art aus. Diese Objekte sind die Elemente der Menge und können sein: Zahlen, Buchstaben, geometrische Figuren, Wörter, die Objekte darstellen, die Objekte selbst und andere.
Es war Georg Cantor, der gegen Ende des 19. Jahrhunderts die Mengenlehre vorschlug. Während andere bemerkenswerte Mathematiker im 20. Jahrhundert ihre Formalisierung machten: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel unter anderem..

Venn-Diagramme sind die grafische Darstellung einer Menge und bestehen aus einer Figur mit geschlossener Ebene, in der sich die Elemente der Menge befinden.
In Abbildung 1 sind beispielsweise zwei Mengen A und B dargestellt, die gemeinsame Elemente haben, die für A und B gemeinsamen Elemente. Diese bilden eine neue Menge, die als Schnittmenge von A und B bezeichnet wird und in der symbolischen Form als geschrieben ist folgt:
A ∩ B.
Artikelverzeichnis
- 1 Funktionen
- 2 Arten von Sets
- 2.1 Endliche Menge
- 2.2 Unendliche Menge
- 2.3 Leerer Satz
- 2.4 Einheitliches Set
- 2.5 Binärsatz
- 2.6 Universalset
- 3 Grundelemente
- 3.1 - Beziehungen zwischen Mengen
- 3.2 - Eigenschaften des Einschlusses
- 3.3 - Operationen zwischen Sätzen
- 4 Beispiele
- 4.1 Beispiel 1
- 4.2 Beispiel 2
- 4.3 Beispiel 3
- 4.4 Beispiel 4
- 4.5 Beispiel 5
- 5 Übungen gelöst
- 5.1 Übung 1
- 5.2 Übung 2
- 5.3 Übung 3
- 5.4 Übung 4
- 6 Referenzen
Eigenschaften
Die Menge ist ein primitives Konzept, da es sich in der Geometrie um das Konzept von Punkt, Linie oder Ebene handelt. Es gibt keinen besseren Weg, um das Konzept auszudrücken, als Beispiele zu nennen:
Set E gebildet durch die Farben der Flagge von Spanien. Diese Art, die Menge auszudrücken, wird durch Verstehen genannt. Die gleiche Menge E, die durch Erweiterung geschrieben wurde, ist:
E = rot, gelb
In diesem Fall sind Rot und Gelb Elemente der Menge E. Es ist zu beachten, dass die Elemente in geschweiften Klammern aufgeführt sind und nicht wiederholt werden. Bei der spanischen Flagge gibt es drei farbige Streifen (rot, gelb, rot), von denen zwei wiederholt werden, aber die Elemente werden nicht wiederholt, wenn der Satz ausgedrückt wird..
Angenommen, die Menge V besteht aus den ersten drei Vokalbuchstaben:
V = a, e, i
Die mit P (V) bezeichnete Potenzmenge von V ist die Menge aller Mengen, die mit den Elementen von V gebildet werden können:
P (V) = a, e, i, a, e, a, i, e, i, a, e, i
Arten von Sets
Endliche Menge
Es ist eine Menge, in der ihre Elemente zählbar sind. Beispiele für endliche Mengen sind unter anderem die Buchstaben des spanischen Alphabets, die Vokale des Spanischen und die Planeten des Sonnensystems. Die Anzahl der Elemente einer endlichen Menge wird als Kardinalität bezeichnet.
Unendliche Menge
Unter einer unendlichen Menge versteht man alles, was die Anzahl ihrer Elemente unzählig macht, da es immer möglich ist, mehr Elemente zu finden, egal wie groß die Anzahl ihrer Elemente sein mag.
Ein Beispiel für eine unendliche Menge ist die Menge der natürlichen Zahlen N, die in umfangreicher Form wie folgt ausgedrückt wird:
N = 1, 2, 3, 4, 5,…. Ist eindeutig eine unendliche Menge, da, egal wie groß eine natürliche Zahl sein mag, die nächstgrößere immer in einem endlosen Prozess gefunden werden kann. Die Kardinalität einer unendlichen Menge ist eindeutig ∞.
Leeres Set
Es ist die Menge, die kein Element enthält. Die leere Menge V wird durch Ø oder durch ein Schlüsselpaar ohne Elemente im Inneren bezeichnet:
V = = Ø.
Die leere Menge ist eindeutig, daher muss es falsch sein, "eine leere Menge" zu sagen. Die richtige Form lautet "die leere Menge"..
Unter den Eigenschaften der leeren Menge haben wir, dass es sich um eine Teilmenge einer beliebigen Menge handelt:
Ø ⊂ A.
Wenn eine Menge eine Teilmenge der leeren Menge ist, ist die Menge notwendigerweise das Vakuum:
A ⊂ Ø ⇔ A = Ø
Einheitliches Set
Ein Einheitensatz ist ein Satz, der ein einzelnes Element enthält. Zum Beispiel ist die Menge der natürlichen Satelliten der Erde eine einheitliche Menge, deren einziges Element der Mond ist. Die Menge B von ganzen Zahlen kleiner als 2 und größer als Null hat nur Element 1, daher ist es eine einheitliche Menge.
Binärsatz
Eine Menge ist binär, wenn sie nur zwei Elemente enthält. Zum Beispiel die Menge X, so dass x eine reelle Zahlenlösung von x ^ 2 = 2 ist. Diese Menge durch Erweiterung ist wie folgt geschrieben:
X = -√2, + √2
universelles Set
Die universelle Menge ist eine Menge, die andere Mengen des gleichen Typs oder der gleichen Art enthält. Zum Beispiel ist die universelle Menge natürlicher Zahlen die Menge reeller Zahlen. Aber die reellen Zahlen sind eine universelle Menge auch der ganzen Zahlen und der rationalen Zahlen.
Kernpunkte
- Beziehungen zwischen Mengen
In Baugruppen können verschiedene Arten von Beziehungen zwischen ihnen und ihren Elementen hergestellt werden. Wenn zwei Mengen A und B genau die gleichen Elemente enthalten, wird eine Gleichheitsbeziehung hergestellt, die wie folgt bezeichnet wird:
ZU = B.
Wenn alle Elemente einer Menge A zu einer Menge B gehören, aber nicht alle Elemente von B zu A gehören, besteht zwischen diesen Mengen eine Einschlussbeziehung, die wie folgt bezeichnet wird:
A ⊂ B, aber B ⊄ A.
Der obige Ausdruck lautet: A ist eine Teilmenge von B, aber B ist keine Teilmenge von A..
Um anzuzeigen, dass einige oder einige Elemente zu einer Menge gehören, wird das Zugehörigkeitssymbol ∈ verwendet, um beispielsweise zu sagen, dass x-Elemente oder Elemente zur Menge gehören. A wird symbolisch wie folgt geschrieben:
x ∈ A.
Wenn ein Element nicht zur Menge A gehört, wird diese Beziehung folgendermaßen geschrieben:
und ∉ A.
Die Zugehörigkeitsbeziehung tritt zwischen den Elementen einer Menge und der Menge auf, mit der einzigen Ausnahme der Potenzmenge, wobei die Potenzmenge die Sammlung oder Menge aller möglichen Mengen ist, die mit den Elementen dieser Menge gebildet werden können.
Angenommen, V = a, e, i, seine Potenzmenge ist P (V) = a, e, i, a, e, a, i, e, i , a, e, i, in diesem Fall wird die Menge V ein Element der Menge P (V) und kann geschrieben werden:
V ∈ P (V)
- Einschlusseigenschaften
Die erste Eigenschaft der Aufnahme legt fest, dass jede Menge in sich selbst enthalten ist, oder mit anderen Worten, dass sie eine Teilmenge von sich selbst ist:
A ⊂ A.
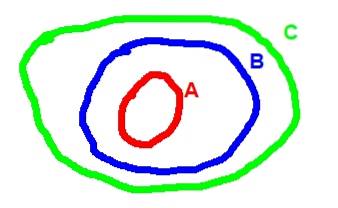
Die andere Eigenschaft des Einschlusses ist die Transitivität: Wenn A eine Teilmenge von B und B wiederum eine Teilmenge von C ist, dann ist A eine Teilmenge von C. In symbolischer Form wird die Transitivitätsbeziehung wie folgt geschrieben:
(A ⊂ B) ^ (B ⊂ C) => A ⊂ C.
Unten ist das Venn-Diagramm, das der Transitivität der Inklusion entspricht:
- Operationen zwischen Sätzen
Überschneidung
Der Schnittpunkt ist eine Operation zwischen zwei Mengen, die zu einer neuen Menge führt, die zu derselben universellen Menge wie die ersten beiden gehört. In diesem Sinne handelt es sich um eine geschlossene Operation.
Symbolisch ist die Kreuzungsoperation wie folgt formuliert:
A⋂B = x / x∈A ^ x∈B
Ein Beispiel ist das Folgende: Die Menge A der Buchstaben des Wortes "Elemente" und die Menge B der Buchstaben des Wortes "wiederholt", der Schnittpunkt zwischen A und B ist wie folgt geschrieben:
A⋂B = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s. Die universelle Menge U von A, von B und auch von A⋂B ist die Menge der Buchstaben des spanischen Alphabets.
Union
Die Vereinigung zweier Mengen ist die Menge, die aus den Elementen besteht, die den beiden Mengen gemeinsam sind, und den nicht gemeinsamen Elementen der beiden Mengen. Die Vereinigungsoperation zwischen Mengen wird symbolisch wie folgt ausgedrückt:
A∪B = x / x∈A v x∈B
Unterschied
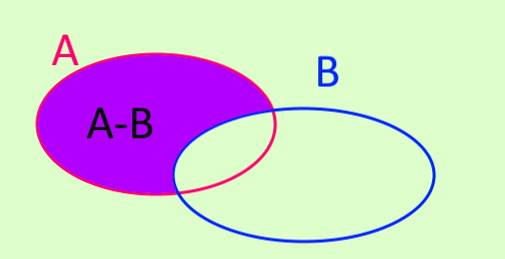
Die Differenzoperation von Satz A minus Satz B wird mit A-B bezeichnet. A-B ist eine neue Menge, die aus allen Elementen besteht, die in A enthalten sind und nicht zu B gehören. Symbolisch ist sie wie folgt geschrieben:
A - B = x / x ∈ A ^ x ∉ B
Symmetrischer Unterschied
Die symmetrische Differenz ist eine Operation zwischen zwei Sätzen, bei der der resultierende Satz aus den Elementen besteht, die den beiden Sätzen nicht gemeinsam sind. Der symmetrische Unterschied wird symbolisch wie folgt dargestellt:
A⊕B = x / x∈ (A-B) ^ x∈ (B-A)
Beispiele
Beispiel 1
Das Venn-Diagramm ist eine grafische Darstellung von Mengen. Zum Beispiel wird die Menge C der Buchstaben in der Wortmenge folgendermaßen dargestellt:

Beispiel 2
Venn-Diagramme zeigen, dass die Menge der Vokale im Wort "Menge" eine Teilmenge der Menge der Buchstaben im Wort "Menge" ist..

Beispiel 3
einstellen Ñ Von den Buchstaben des spanischen Alphabets ist eine endliche Menge, diese Menge durch Erweiterung ist wie folgt geschrieben:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z und seine Kardinalität ist 27.
Beispiel 4
einstellen V. der Vokale auf Spanisch ist eine Teilmenge der Menge Ñ:
V. ⊂ Ñ daher ist es eine endliche Menge.
Die endliche Menge V. in umfangreicher Form ist es so geschrieben: V. = a, e, i, o, u und seine Kardinalität ist 5.
Beispiel 5
Ausgehend von den Mengen A = 2, 4, 6, 8 und B = 1, 2, 4, 7, 9 bestimmen Sie A-B und B-A.
A - B sind die Elemente von A, die nicht in B sind:
A - B = 6, 8
B - A sind die Elemente von B, die nicht in A enthalten sind:
B - A = 1, 7, 9
Gelöste Übungen
Übung 1
Schreiben Sie in symbolischer Form und auch in Erweiterung die Menge P von geraden natürlichen Zahlen kleiner als 10.
Lösung: P = x∈ N / x < 10 ^ x mod 2 = 0
P = 2, 4, 6, 8
Übung 2
Angenommen, die Menge A, die durch die natürlichen Zahlen gebildet wird, die Faktoren von 210 sind, und die Menge B, die durch die natürlichen Primzahlen kleiner als 9 gebildet wird. Bestimmen Sie durch Erweiterung beide Mengen und stellen Sie fest, welche Beziehung zwischen den beiden Mengen besteht.
Lösung: Um die Elemente der Menge A zu bestimmen, müssen wir zunächst die Faktoren der natürlichen Zahl 210 finden:
210 = 2 * 3 * 5 * 7
Dann wird die Menge A geschrieben:
A = 2, 3, 5, 7
Wir betrachten nun die Menge B, bei der es sich um Primzahlen unter 9 handelt. 1 ist keine Primzahl, da sie nicht der Definition der Primzahl entspricht: „Eine Zahl ist genau dann eine Primzahl, wenn sie genau zwei Teiler hat, 1 und die Zahl selbst.“ . Die 2 ist gerade und gleichzeitig eine Primzahl, weil sie der Definition einer Primzahl entspricht. Die anderen Primzahlen unter 9 sind 3, 5 und 7. Die Menge B lautet also:
B = 2, 3, 5, 7
Daher sind die beiden Sätze gleich: A. = B..
Übung 3
Bestimmen Sie die Menge, deren Elemente x sich von x unterscheiden.
Lösung: C = x / x ≠ x
Da jedes Element, jede Zahl oder jedes Objekt gleich sich selbst ist, kann die Menge C nicht anders sein als die leere Menge:
C = Ø
Übung 4
Die Menge der Ns natürlicher Zahlen und Z sei die Menge der ganzen Zahlen. Bestimmen Sie N ⋂ Z und N ∪ Z..
Lösung:
N ≤ Z = x ≤ Z / x ≤ 0 = (-∞, 0]
N ≤ Z = Z, weil N ≤ Z..
Verweise
- Garo, M. (2014). Mathematik: quadratische Gleichungen: Wie man eine quadratische Gleichung löst. Marilù Garo.
- Haeussler, E. F. & Paul, R. S. (2003). Mathematik für Management und Wirtschaft. Pearson Ausbildung.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Mathematik 1 SEP. Schwelle.
- Preciado, C. T. (2005). Mathematikkurs 3 .. Editorial Progreso.
- Mathematics 10 (2018). "Beispiele für endliche Mengen". Wiederhergestellt von: matematicas10.net
- Wikipedia. Mengenlehre. Wiederhergestellt von: es.wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.