
Oktalsystemverlauf, Nummerierungssystem, Konvertierungen
Das Oktalsystem ist ein Basis-Acht (8) -Positionsnummerierungssystem; Das heißt, es besteht aus acht Ziffern: 0, 1, 2, 3, 4, 5, 6 und 7. Daher kann jede Ziffer einer Oktalzahl einen beliebigen Wert von 0 bis 7 haben. Die Oktalzahlen werden gebildet aus Binärzahlen.
Dies ist so, weil seine Basis eine exakte Zweierpotenz ist (2). Das heißt, die Zahlen, die zum Oktalsystem gehören, werden gebildet, wenn sie in drei aufeinanderfolgende Ziffern gruppiert werden, die von rechts nach links geordnet sind, wodurch ihr Dezimalwert erhalten wird..

Artikelverzeichnis
- 1 Geschichte
- 2 Oktal-Nummerierungssystem
- 3 Konvertierung vom Oktal- zum Dezimalsystem
- 3.1 Beispiel 1
- 3.2 Beispiel 2
- 4 Konvertierung vom Dezimal- zum Oktalsystem
- 4.1 Beispiel
- 5 Konvertierung vom Oktal- zum Binärsystem
- 6 Konvertierung vom binären zum oktalen System
- 7 Umrechnung von oktal nach hexadezimal und umgekehrt
- 7.1 Beispiel
- 8 Referenzen
Geschichte
Das Oktalsystem hat seinen Ursprung in der Antike, als Menschen mit ihren Händen Tiere von acht bis acht zählten.
Um zum Beispiel die Anzahl der Kühe in einem Stall zu zählen, begann man mit der rechten Hand zu zählen und verband den Daumen mit dem kleinen Finger; Um dann das zweite Tier zu zählen, wurde der Daumen mit dem Zeigefinger usw. mit den verbleibenden Fingern jeder Hand verbunden, bis 8 abgeschlossen war.
Es besteht die Möglichkeit, dass in der Antike das oktale Nummerierungssystem vor der Dezimalstelle verwendet wurde, um Interdigitalräume zählen zu können; d.h. alle Finger außer Daumen zählen.
Später wurde das oktale Nummerierungssystem eingerichtet, das aus dem Binärsystem stammt, da es viele Ziffern benötigt, um nur eine Zahl darzustellen. Von da an wurden die oktalen und hexagonalen Systeme erstellt, die nicht so viele Ziffern benötigen und leicht in das Binärsystem konvertiert werden können.
Oktal-Nummerierungssystem
Das Oktalsystem besteht aus acht Ziffern von 0 bis 7. Diese haben den gleichen Wert wie im Fall des Dezimalsystems, aber ihr relativer Wert ändert sich abhängig von der Position, die sie einnehmen. Der Wert jeder Position wird durch die Potenzen der Basis 8 angegeben.
Die Positionen der Ziffern in einer Oktalzahl haben die folgenden Gewichte:
84, 83, 8zwei, 81, 80, Oktalpunkt, 8-1, 8-zwei, 8-3, 8-4, 8-5.
Die größte Oktalstelle ist 7; Auf diese Weise wird beim Zählen in diesem System die Position einer Ziffer von 0 auf 7 erhöht. Wenn 7 erreicht ist, wird sie für die nächste Zählung auf 0 zurückgeführt. Auf diese Weise wird die nächste Ziffernposition erhöht. Zum Beispiel, um Sequenzen zu zählen, wird es im Oktalsystem sein:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
Es gibt einen fundamentalen Satz, der auf das Oktalsystem angewendet wird und wie folgt ausgedrückt wird:
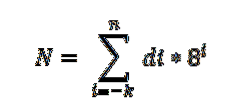
In diesem Ausdruck repräsentiert di die Ziffer multipliziert mit der Potenz der Basis 8, die den Stellenwert jeder Ziffer auf dieselbe Weise angibt, wie sie im Dezimalsystem geordnet ist.
Zum Beispiel haben Sie die Nummer 543.2. Um es zum Oktalsystem zu bringen, wird es wie folgt aufgeteilt:
N = ∑ [(5 * * 8zwei) + (4 * * 81) + (3 * *80) + (2 * *8-1)] = (5 · 64) + (4 · 8) + (2 · 1) + (2 · 0,125)
N = 320 + 32 + 2 + 0,25 = 354 + 0,25d
Auf diese Weise müssen Sie 543.2Was = 354,25d. Der Index q gibt an, dass es sich um eine Oktalzahl handelt, die auch durch die Zahl 8 dargestellt werden kann. und der Index d bezieht sich auf die Dezimalzahl, die auch durch die Zahl 10 dargestellt werden kann.
Konvertierung vom Oktal- zum Dezimalsystem
Um eine Zahl aus dem Oktalsystem in ihre Entsprechung im Dezimalsystem umzuwandeln, müssen Sie nur jede Oktalziffer beginnend von rechts mit ihrem Stellenwert multiplizieren.
Beispiel 1
7328 = (7* * 8zwei) + (3* * 81) + (2* * 80) = (7 * * 64) + (3 * * 8) + (2 * * 1)
7328= 448 +24 +2
7328= 47410
Beispiel 2
26.98 = (2 * *81) + (6* * 80) + (9* * 8-1) = (2 * * 8) + (6 * * 1) + (9 * * 0,125)
26.98 = 16 + 6 + 1,125
26.98= 23.12510
Konvertierung vom Dezimal- zum Oktalsystem
Eine Dezimalzahl kann unter Verwendung der Methode der wiederholten Division in eine Oktalzahl umgewandelt werden, wobei die Dezimalzahl durch 8 geteilt wird, bis der Quotient gleich 0 ist, und die verbleibenden Reste jeder Division die Oktalzahl darstellen..
Die Residuen werden vom letzten zum ersten geordnet; Das heißt, der erste Rest ist die niedrigstwertige Ziffer der Oktalzahl. Auf diese Weise ist die höchstwertige Ziffer der letzte Rest..
Beispiel
Oktal der Dezimalzahl 26610
- Teilen Sie die Dezimalzahl 266 durch 8 = 266/8 = 33 + Rest von 2.
- Teilen Sie dann die 33 durch 8 = 33/8 = 4 + Rest von 1.
- Teilen Sie 4 durch 8 = 4/8 = 0 + Rest von 4.
Da mit der letzten Division ein Quotient kleiner als 1 erhalten wird, bedeutet dies, dass das Ergebnis gefunden wurde; Sie müssen die Reste nur umgekehrt anordnen, so dass die Oktalzahl der Dezimalstelle 266 412 beträgt, wie im folgenden Bild zu sehen ist:
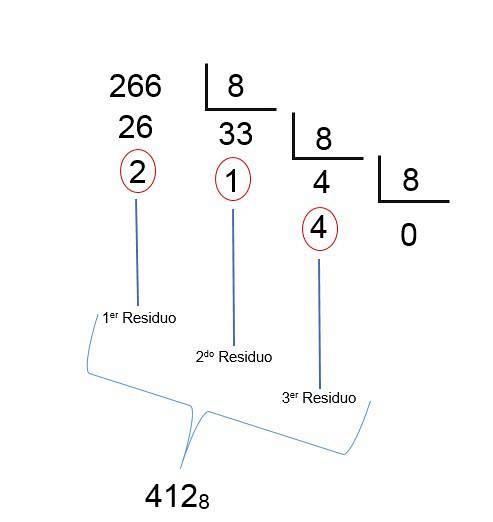
Konvertierung vom Oktal- zum Binärsystem
Die Konvertierung von oktal nach binär erfolgt durch Konvertierung der oktalen Ziffer in die entsprechende binäre Ziffer, die aus drei Ziffern besteht. Es gibt eine Tabelle, die zeigt, wie die acht möglichen Ziffern konvertiert werden:
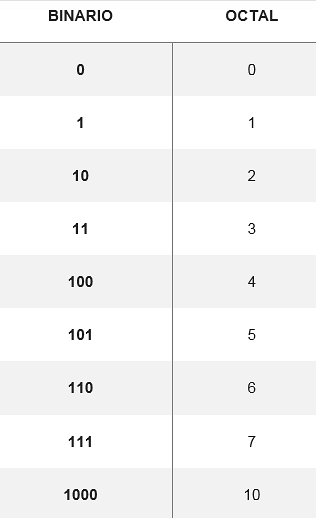
Aus diesen Konvertierungen können Sie eine beliebige Zahl aus dem Oktalsystem in eine Binärzahl ändern, um beispielsweise die Zahl 572 umzuwandeln8 Ihre Entsprechungen werden in der Tabelle gesucht. Also muss es:
58 = 101
78= 111
zwei8 = 10
Daher 5728 entspricht im Binärsystem 10111110.
Konvertieren von binär nach oktal
Der Prozess des Konvertierens von binären Ganzzahlen in oktale Ganzzahlen ist die inverse Operation des vorherigen Prozesses.
Das heißt, die Bits der Binärzahl werden von rechts nach links in zwei Gruppen von drei Bits gruppiert. Dann erfolgt die Konvertierung von binär nach oktal mit der vorherigen Tabelle.
In einigen Fällen hat die Binärzahl keine Gruppen von 3 Bits; Um dies zu vervollständigen, werden links von der ersten Gruppe ein oder zwei Nullen hinzugefügt.
Gehen Sie beispielsweise wie folgt vor, um die Binärzahl 11010110 in Oktal zu ändern:
- Gruppen von 3 Bits werden beginnend von rechts (letztes Bit) gebildet:
11010110
- Da die erste Gruppe unvollständig ist, wird eine führende Null hinzugefügt:
011010110
- Die Konvertierung erfolgt aus der Tabelle:
011 = 3
010 = 2
110 = 6
Somit ist die Binärzahl 011010110 gleich 3268.
Konvertieren von oktal nach hexadezimal und umgekehrt
Um von einer Oktalzahl zum Hexadezimalsystem oder von einer Hexadezimalzahl zum Oktalsystem zu wechseln, muss die Zahl zuerst in eine Binärzahl und dann in das gewünschte System konvertiert werden.
Hierzu gibt es eine Tabelle, in der jede hexadezimale Ziffer mit ihrem Äquivalent im Binärsystem dargestellt wird, das aus vier Ziffern besteht.
In einigen Fällen hat die Binärzahl keine Gruppen von 4 Bits. Um dies zu vervollständigen, werden links von der ersten Gruppe ein oder zwei Nullen hinzugefügt
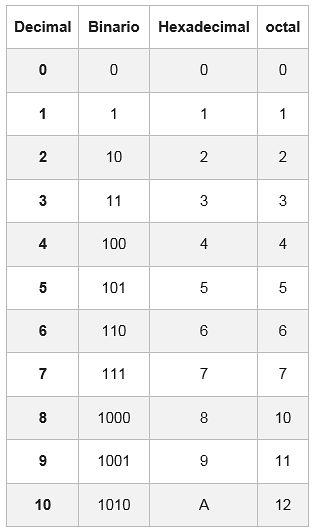
Beispiel
Konvertieren Sie die Oktalzahl 1646 in eine Hexadezimalzahl:
- Konvertieren Sie die Zahl von oktal in binär
18 = 1
68 = 110
48 = 100
68 = 110
- So 16468 = 1110100110.
- Um von binär nach hexadezimal zu konvertieren, werden sie zunächst in einer Gruppe von 4 Bits von rechts nach links angeordnet:
11 1010 0110
- Die erste Gruppe wird mit Nullen vervollständigt, so dass sie 4 Bits haben kann:
0011 1010 0110
- Die Konvertierung erfolgt vom binären zum hexadezimalen System. Die Äquivalenzen werden durch die Tabelle ersetzt:
0011 = 3
1010 = A.
0110 = 6
Somit entspricht die Oktalzahl 1646 3A6 im Hexadezimalsystem..
Verweise
- Bressan, A. E. (1995). Einführung in Nummerierungssysteme. Argentinische Wirtschaftsuniversität.
- Harris, J. N. (1957). Einführung in die binären und oktalen Nummerierungssysteme: Lexington, Mass. Armed Services Technical Information Agency.
- Kumar, A. A. (2016). Grundlagen digitaler Schaltungen. Lernen Pvt.
- Peris, X. C. (2009). Einzelne Betriebssysteme.
- Ronald J. Tocci, N. S. (2003). Digitale Systeme: Prinzipien und Anwendungen. Pearson Ausbildung.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.