Das Vektorsubtraktion oder Vektorsubtraktion zwischen Vektoren oder Y. v bezeichnet durch oder - v, wird durch Addition des Vektors berechnet oder mit dem gegenüberliegenden Vektor v. Algebraisch wird die Subtraktion wie folgt ausgedrückt:
oder - v = oder + ((-v)
Es ist möglich, eine Vektorsubtraktion nach verschiedenen Verfahren durchzuführen, beispielsweise grafisch, auf diese Weise einen Vektor v wird durch ein orientiertes Liniensegment gezeichnet - einen Pfeil-.
Die Länge des Pfeils entspricht dem Modul des Vektors, die Neigung - in Bezug auf eine gegebene Referenzlinie - gibt die Richtung an und das Ende gibt die Richtung des Vektors an.
Der gegenüberliegende Vektor v es hat die gleiche Länge und Richtung, aber die entgegengesetzte Richtung. Dann, bevor Sie die Subtraktion zwischen machen oder Y. v, es ist notwendig, den gegenüberliegenden Vektor zu zeichnen v, und füge diesen Vektor zu u hinzu.
Es ist sehr wichtig zu beachten, dass die Vektorsubtraktion nicht kommutativ ist, dh die Reihenfolge der Vektoren ändert das Ergebnis, daher:
oder - v ≠ v - oder
Das grafische Verfahren kann mit einer dieser Methoden ausgeführt werden, deren Schritte im Folgenden erläutert werden:
-Dreiecksmethode.
-Parallelogrammmethode.
Artikelverzeichnis
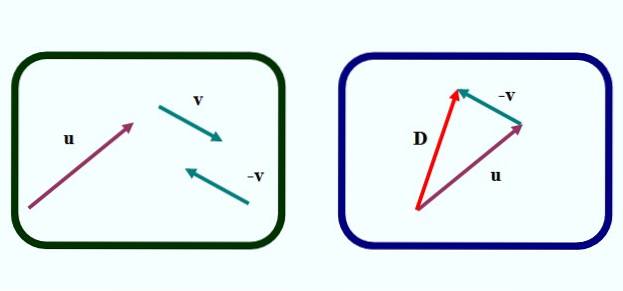
In Abbildung 1 haben wir die erste Methode, um zwei Vektoren grafisch zu subtrahieren. Es geht um Dreiecksmethode, weil die Figur, die durch Festlegen der Vektoren gebildet wird, ein Dreieck ist, wie wir im linken Bild sehen können.
Subtraktion durchführen oder - v Wir gehen wie folgt vor:
-Zeichnen Sie den Vektor -v vom Vektor v, durch Übersetzung mit einem Lineal und einem Quadrat, aber Ändern der Pfeilrichtung (linkes Bild).
-Wechselt zum Vektor -v so, dass sein Ursprung mit dem Ende des Vektors übereinstimmt oder (rechtes Bild).
-Als nächstes wird ein Vektor gezeichnet (im rechten Bild rot), der vom Ursprung von ausgeht oder bis zum Ende von v. Anruf D. y ist der Differenzvektor:
D. = oder - v
Bei der Parallelogrammmethode müssen die zu addierenden oder zu subtrahierenden Vektoren an ihren Ursprungspunkten zusammenfallen. Angenommen, wir wollen finden oder - v Mit unseren oben gezeigten Vektoren sind die Schritte zum Finden der Subtraktion von Vektoren durch dieses Verfahren wie folgt:
-Bestimmen Sie den gegenüberliegenden Vektor v, Was ist es -v, wie oben für die Dreiecksmethode beschrieben.
-Vektoren sorgfältig übersetzen oder Y. -v so, dass ihre Ursprünge zusammenfallen.
-Jetzt werden segmentierte parallele Linien beginnend an den Enden jedes Vektors gezeichnet. Die gebildete Figur ist ein Parallelogramm und in besonderen Fällen, in denen die Vektoren senkrecht sind, ergibt sich ein Rechteck oder ein Quadrat..
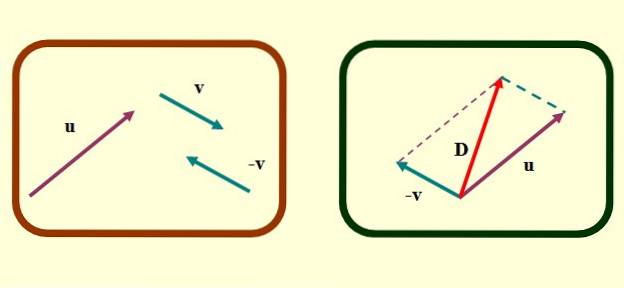
-Schließlich wird ein Vektor gezeichnet, der vom gemeinsamen Ursprung von ausgeht oder Y. v bis zum Äußersten, wo sich die segmentierten parallelen Linien schneiden. Dies ist der Vektor D. oder Subtraktion.
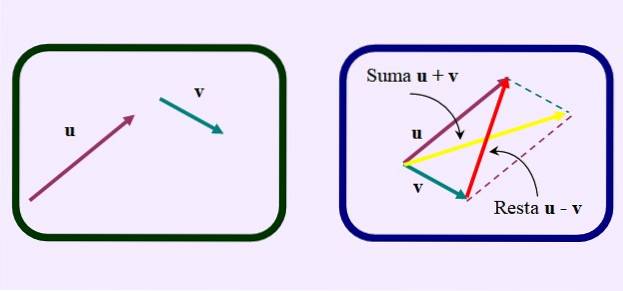
Eine andere Möglichkeit, die Subtraktion durchzuführen, besteht darin, das Parallelogramm so zu zeichnen, als ob Sie die Vektoren hinzufügen möchten.
Aber anstatt die übliche Diagonale der Summe zu zeichnen, die vom gemeinsamen Ursprung bis zum Schnittpunkt der Parallelen reicht, wird die entgegengesetzte oder kürzere Diagonale, wie in der Abbildung zu sehen:
Ein Schiff segelt auf einem Fluss und dies entgegen der Strömung. Ein Beobachter an Land beobachtet, dass die Geschwindigkeit des Bootes aufgrund der Wirkung der Strömung verringert wird.
Die Geschwindigkeit ist ein Vektor und in diesem Beispiel zeigt die Geschwindigkeit des Bootes in eine Richtung und die Geschwindigkeit der Strömung hat dieselbe Richtung und entgegengesetzte Richtung. Die Nettogeschwindigkeit des Schiffes ist die Summe beider Vektoren.
Wenn beispielsweise die Instrumente des Bootes anzeigen, dass es sich mit v '= + 40 km / h bewegt, und ein Beobachter am Ufer misst, dass sich das Boot mit v = + 30 km / h bewegt. Da v = v '+ Vc, wobei Vc die Geschwindigkeit des Stroms ist, der durch Subtrahieren der Geschwindigkeiten v bzw. v' berechnet wird: Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.
In der Kinematik haben wir wichtige Vektoren, die Änderungen beschreiben:
-Offset für Positionsänderungen.
-Durchschnittsgeschwindigkeit, um zu quantifizieren, wie schnell sich die Position im Laufe der Zeit ändert.
-Beschleunigung für Geschwindigkeitsänderungen in Abhängigkeit von der Zeit.
Der Verschiebungsvektor beschreibt die Positionsänderung, die ein Körper während seiner Bewegung erfährt.
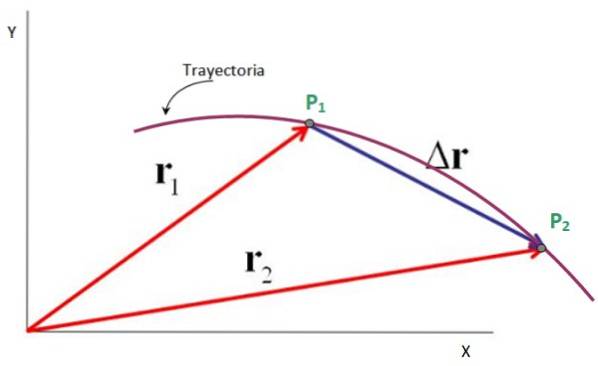
Sehen wir uns zum Beispiel ein Teilchen an, das den in der Abbildung gezeigten ebenen Pfad beschreibt, in dem es vom Punkt P aus verläuft1 zu Punkt P.zwei.
Die Vektoren, die vom Ursprung des x-y-Koordinatensystems zu diesen Punkten gerichtet sind, sind die Positionsvektoren r1 Y. rzwei, während der Verschiebungsvektor Δ istr, das geht von P.1 obenzwei. Es stimmt, dass:
Δr = rzwei - r1
Daher ist der Verschiebungsvektor die Subtraktion zwischen dem Endpositionsvektor und dem Anfangspositionsvektor, wie in der folgenden Abbildung gezeigt. Seine Einheiten sind auch die der Position: Meter, Fuß, Meilen, Zentimeter und mehr..
Der mittlere Geschwindigkeitsvektor seinerseits vm ist definiert als der Versatz multipliziert mit der Umkehrung des Zeitintervalls:
Ein Teilchen, das einen Kreis beschreibt, benötigt 5 s, um von Punkt A nach Punkt B zu gelangen. Bei A hat es eine Geschwindigkeit vZU = 60 km / h in Richtung der + x-Achse und bei B ist vB. = 60 km / h in Richtung + y. Bestimmen Sie die durchschnittliche Beschleunigung grafisch und analytisch.
In grafischer Form werden Richtung und Richtung der mittleren Beschleunigung bestimmt durch:
Im folgenden Bild ist die Subtraktion vB. - vZU, mit der Dreiecksmethode, da die durchschnittliche Beschleunigung zum ist proportional zu Δv. Das gebildete Dreieck hat die beiden Beine gleich und daher messen die spitzen Innenwinkel jeweils 45º..
Analytisch, wenn die + x-Richtung mit dem Einheitsvektor übereinstimmt ich und die + y-Richtung mit dem Einheitsvektor j, dann:
Δv = 60 km / h j - 60 km / h ich
Unter Berücksichtigung von Δt = 5 s beträgt die mittlere Beschleunigung gemäß den Angaben in der Aussage:
zum = (60 km / h j - 60 km / h ich) / 5 s = 12 (j-ich) km / (h.s)
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.