Proportionalitätsbeziehungskonzept, Beispiele und Übungen

Das Verhältnismäßigkeitsbeziehungen Sie sind Verknüpfungen zwischen zwei oder mehr Variablen, so dass, wenn eine der Größen variiert, auch der Wert der anderen variiert. Wenn zum Beispiel einer zunimmt, können die anderen zunehmen oder abnehmen, jedoch in einer einheitlichen Menge..

Altgriechische Mathematiker erkannten, dass einige Variablen sehr genau miteinander verbunden waren. Sie erkannten, dass ein Kreis, der doppelt so groß wie der Durchmesser eines anderen ist, einen doppelt so großen Umfang hat.

Und wenn sich der Durchmesser verdreifacht, verdreifacht sich auch die Kontur des Umfangs. Dies bedeutet, dass eine Vergrößerung des Durchmessers eine proportionale Vergrößerung des Umfangs bewirkt..

Und so können wir bestätigen, dass die Länge des Umfangs L proportional zu seinem Durchmesser D ist, der wie folgt ausgedrückt wird:

L ∝ D.

Wo das Symbol ∝ lautet "direkt proportional zu”. Um das Symbol der Proportionalität in das Symbol der Gleichheit zu ändern und numerische Werte einzubeziehen, muss die Verbindung zwischen den aufgerufenen Variablen bestimmt werden Proportionalitätskonstante.

Nach vielen Messungen stellten die alten Mathematiker fest, dass die Proportionalitätskonstante zwischen der Größe L des Umfangs und dem Durchmesser D derselben die Zahl 3,1416 war ... Die Ellipsen geben eine unendliche Anzahl von Dezimalstellen an.

Dieser Wert ist nichts anderes als die berühmte Zahl π (pi) und auf diese Weise schreiben wir:

L = π.D

Auf diese Weise ist das Verhältnis der Länge zum Durchmesser eines Umfangs das gleiche wie das Verhältnis der Länge zum Durchmesser eines anderen. Und das Beste ist, dass wir jetzt die Länge eines Umfangs berechnen können, indem wir nur seinen Durchmesser kennen.

Artikelverzeichnis

• 1 Beispiele für Verhältnismäßigkeitsbeziehungen
• 2 Direkte Proportionalität und inverse Proportionalität
• 3 Andere Arten der Verhältnismäßigkeit
• 4 Übungen
  • 4.1 - Übung 1
  • 4.2 - Übung 2
• 5 Referenzen

Beispiele für Verhältnismäßigkeitsbeziehungen

In der Wissenschaft (und auch im Alltag) ist es sehr wichtig, Beziehungen zwischen Variablen zu finden, um zu wissen, wie sich Änderungen in einer von ihnen auf die andere auswirken. Beispielsweise:

-Wenn Sie 3 Tassen Mehl benötigen, um ein Dutzend Kekse zu machen. Wie viele Tassen braucht man, um zweieinhalb Dutzend zu machen??.

-Wenn man weiß, dass ein Objekt auf dem Planeten Merkur viermal weniger wiegt als auf der Erde, wie viel wiegt ein 1,5-Tonnen-Auto auf Merkur??

-Wie wirkt sich die Änderung der ausgeübten Kraft auf die Beschleunigung des Körpers aus, auf den sie ausgeübt wird??

-Wenn ein Fahrzeug auf einer Autobahn mit gleichmäßiger geradliniger Bewegung fährt und wir wissen, dass es in 10 Minuten 30 km zurücklegt, wie hoch ist die zurückgelegte Strecke nach 20 Minuten??

-Wenn wir einen Draht haben, durch den ein elektrischer Strom fließt, wie ändert sich die Spannung zwischen ihren Enden, wenn sie ansteigt??

-Wenn der Durchmesser eines Kreises verdoppelt wird, wie wird seine Fläche beeinflusst??

-Wie wirkt sich die Entfernung auf die Intensität des elektrischen Feldes aus, das durch eine Punktladung erzeugt wird??

Die Antwort liegt in Proportionalitätsbeziehungen, aber nicht alle Beziehungen sind vom gleichen Typ. Dann finden wir sie für alle hier angesprochenen Situationen.

Direkte Proportionalität und inverse Proportionalität

Zwei Variablen x und y stehen in direktem Verhältnis, wenn sie miteinander verbunden sind:

y = kx

Wobei k die Proportionalitätskonstante ist. Ein Beispiel ist die Beziehung zwischen den Mengen an Mehl und Keksen. Wenn wir diese Variablen grafisch darstellen, erhalten wir eine gerade Linie wie die in der Abbildung gezeigte:

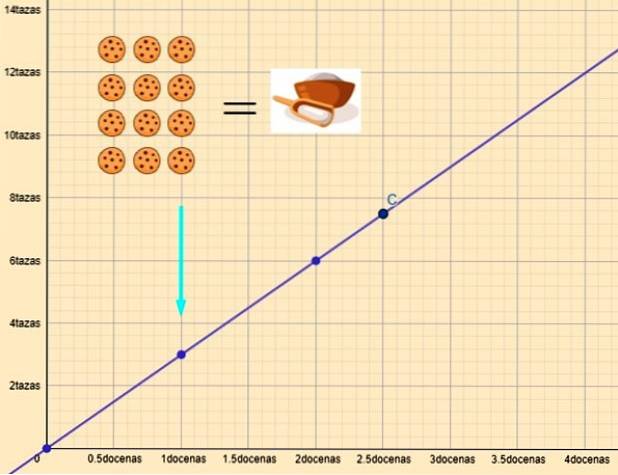
Wenn y die Tassen Mehl und x das Dutzend Kekse sind, ist die Beziehung zwischen ihnen:

y = 3x

Für x = 1 Dutzend benötigen wir y = 3 Tassen Mehl. Und für x = 2,5 Dutzend sind y = 7,5 Tassen Mehl erforderlich.

Wir haben aber auch:

-Beschleunigung zu dass ein Körper erlebt, ist proportional zur Kraft F. darauf einwirken, die Masse des Körpers sein, genannt m, die Konstante der Verhältnismäßigkeit:

F. = mzu

Je größer die ausgeübte Kraft ist, desto größer ist daher die erzeugte Beschleunigung..

-Bei ohmschen Leitern ist die Spannung V zwischen ihren Enden proportional zum angelegten Strom I. Die Proportionalitätskonstante ist der Widerstand R des Leiters:

V = RI

-Wenn sich ein Objekt mit gleichmäßiger geradliniger Bewegung bewegt, ist die Entfernung d ist proportional zur Zeit t, die Geschwindigkeit sein v die Konstante der Verhältnismäßigkeit:

d = v.t.

Manchmal finden wir zwei Größen, so dass eine Zunahme in einer a erzeugt verringern proportional in der anderen. Diese Abhängigkeit wird aufgerufen inverses Verhältnis.

Zum Beispiel ist in der vorherigen Gleichung die Zeit t, die erforderlich ist, um eine bestimmte Strecke d zurückzulegen, umgekehrt proportional zur Geschwindigkeit v der Fahrt:

t = d / v

Und so während höher ist die Geschwindigkeit v, Weniger Zeit, die das Auto benötigt, um die Strecke zurückzulegen d. Wenn zum Beispiel die Geschwindigkeit verdoppelt wird, halbiert sich die Zeit.

Wenn zwei Variablen x und y umgekehrt proportional sind, können wir schreiben:

y = k / x

K ist die Konstante der Proportionalität. Der Graph dieser Abhängigkeit ist:

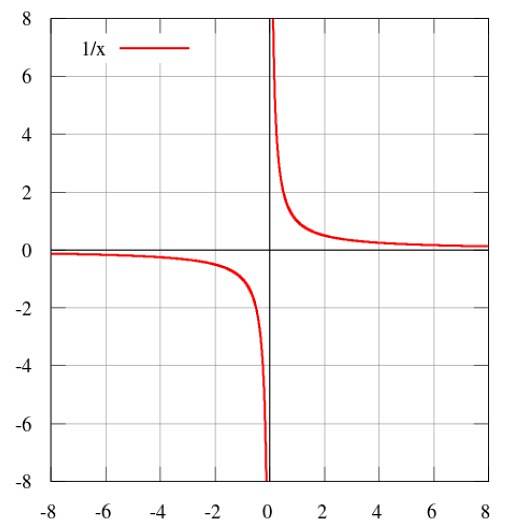
Andere Arten der Verhältnismäßigkeit

In einem der zuvor erwähnten Beispiele haben wir uns gefragt, was mit der Fläche des Kreises passiert, wenn der Radius zunimmt. Die Antwort ist, dass die Fläche direkt proportional zum Quadrat des Radius ist, wobei π die Proportionalitätskonstante ist:

A = πR^zwei

Wenn der Radius verdoppelt wird, vergrößert sich die Fläche um den Faktor 4.

Und im Falle des elektrischen Feldes UND erzeugt durch eine Punktladung Was, Es ist bekannt, dass die Intensität mit der Umkehrung des Quadrats der Entfernung abnimmt r zur Last Was::

E = k_und q / r^zwei

Wir können aber auch sagen, dass die Intensität des Feldes direkt proportional zur Größe der Ladung ist und die Proportionalitätskonstante k ist_und, die elektrostatische Konstante.

Andere Proportionalitäten, die ebenfalls in Science vorgestellt werden, sind exponentielle Proportionalität und logarithmische Proportionalität. Im ersten Fall hängen die Variablen x und y zusammen mit:

y = k.a.^x

Wenn a die Basis ist, eine andere positive Zahl als 0, die normalerweise 10 ist, oder die Zahl e. Zum Beispiel hat das exponentielle Wachstum von Bakterien diese Form.

Im zweiten Fall ist die Beziehung zwischen den Variablen:

y = k.log_zu x

Wieder ist a die Basis des Logarithmus, der oft 10 (dezimaler Logarithmus) oder e (natürlicher Logarithmus) ist..

Ausbildung

- Übung 1

Wenn man weiß, dass ein Objekt auf dem Planeten Merkur viermal weniger wiegt als auf der Erde, wie viel würde ein 1,5-Tonnen-Auto auf Merkur wiegen??

Lösung  

Gewicht auf Quecksilber = (1/4) Gewicht auf der Erde = (1/4) x 1,5 Tonnen = 0,375 Tonnen.

- Übung 2

Für eine Party beschließen einige Freunde, Saft aus Fruchtkonzentrat zuzubereiten. Die Anweisungen auf der Verpackung besagen, dass ein Glas Konzentrat 15 Gläser Saft ergibt. Wie viel Konzentrat wird benötigt, um 110 Gläser Saft herzustellen??

Lösung

Sei y die Anzahl der Gläser Saft und x die Anzahl der Gläser Konzentrat. Sie sind verwandt mit:

y = kx

Durch Ersetzen der Werte y = 15 und x = 1 wird die Konstante k gelöst:

k = y / x = 15/1 = 15

Deshalb:

110 = 15 x

x = 110/15 = 7,33 Gläser Fruchtkonzentrat.

Verweise

1. Baldor, A. 1974. Algebra. Kultur Venezolana S.A..
2. Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
3. Uni-Tutoren. Proportionalitätsbeziehungen. Wiederhergestellt von: varsitytutors.com
4. Wikipedia. Verhältnismäßigkeit Wiederhergestellt von: es.wikipedia.org.
5. Zill, D. 1984. Algebra und Trigonometrie. Mcgraw Hügel.