
Rechte Regel erste und zweite Regel, Anwendungen, Übungen

Das rechte Regel ist eine mnemonische Ressource, um die Richtung und den Sinn des Vektors zu bestimmen, die sich aus einem Vektorprodukt oder Kreuzprodukt ergeben. Es ist in der Physik weit verbreitet, da es wichtige Vektorgrößen gibt, die das Ergebnis eines Vektorprodukts sind. Dies ist beispielsweise der Fall bei Drehmoment, Magnetkraft, Drehimpuls und magnetischem Moment.
Sei zwei generische Vektoren zu Y. b dessen Kreuzprodukt ist zu x b. Das Modul eines solchen Vektors ist:
zu x b = a.b. in α
Wobei α der minimale Winkel zwischen ist zu Y. b, während a und b seine Module darstellen. Zur Unterscheidung der Vektoren ihrer Module werden fette Buchstaben verwendet.
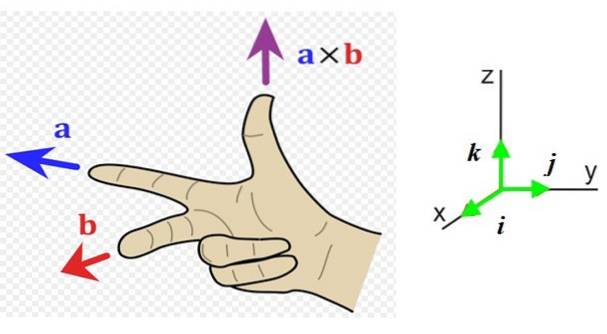
Jetzt müssen wir die Richtung und den Sinn dieses Vektors kennen, daher ist es zweckmäßig, ein Referenzsystem mit den drei Raumrichtungen zu haben (Abbildung 1 rechts). Die Einheitsvektoren ich, j Y. k Sie zeigen jeweils auf den Leser (von der Seite) nach rechts und oben.
Im Beispiel in Abbildung 1 links der Vektor zu geht nach links (Richtung Y. Negativ und Zeigefinger der rechten Hand) und des Vektors b geht zum Leser (Richtung x positiv, Mittelfinger der rechten Hand).
Der resultierende Vektor zu x b hat die Daumenrichtung nach oben in die Richtung z positiv.
Artikelverzeichnis
- 1 Zweite Regel der rechten Hand
- 1.1 Alternative Regel der rechten Hand
- 2 Anwendungen
- 2.1 Winkelgeschwindigkeit und Beschleunigung
- 2.2 Der Drehimpuls
- 3 Übungen
- 3.1 - Übung 1
- 3.2 - Übung 2
- 4 Referenzen
Zweite Regel der rechten Hand
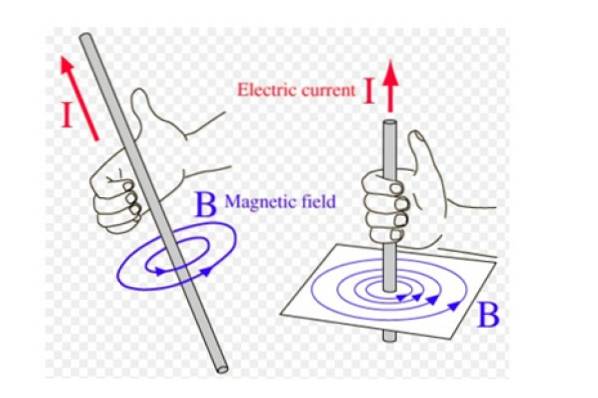
Diese Regel wird auch genannt rechte Daumenregel, Es wird häufig verwendet, wenn es Größen gibt, deren Richtung und Richtung sich drehen, wie z. B. das Magnetfeld B. erzeugt durch einen dünnen, geraden Draht, der einen Strom führt.
In diesem Fall sind die Magnetfeldlinien konzentrische Kreise mit dem Draht, und die Drehrichtung wird mit dieser Regel folgendermaßen erhalten: Der rechte Daumen zeigt in Stromrichtung und die verbleibenden vier Finger sind in Richtung gekrümmt die Landschaft. Wir veranschaulichen das Konzept in Abbildung 2.
Alternative Rechtsregel
Die folgende Abbildung zeigt eine alternative Form der rechten Regel. Die in der Abbildung gezeigten Vektoren sind:
-Geschwindigkeit v einer Punktladung q.
-Magnetfeld B. innerhalb dessen sich die Last bewegt.
-F.B. die Kraft, die das Magnetfeld auf die Ladung ausübt.
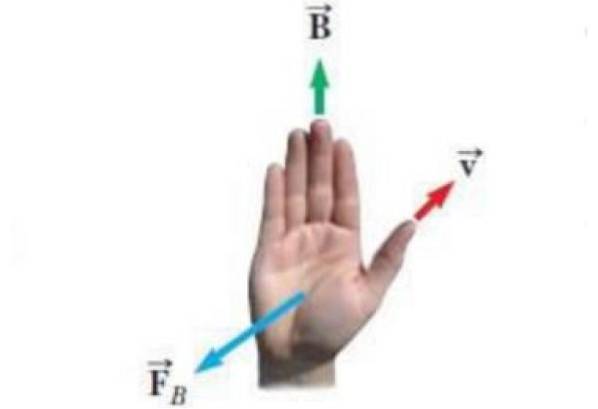
Die Gleichung für die Magnetkraft lautet F.B. = qv x B. und die Regel der rechten Hand, die Richtung und den Sinn von zu kennen F.B. wird wie folgt angewendet: Der Daumen zeigt gemäß v, die vier verbleibenden Finger werden gemäß Feld B platziert. Dann F.B. ist ein Vektor, der senkrecht dazu aus der Handfläche kommt, als würde er die Last drücken.
Beachten Sie, dass F.B. Ich würde in die entgegengesetzte Richtung zeigen wenn die Ladung q negativ war, da das Vektorprodukt nicht kommutativ ist. Tatsächlich:
zu x b = - b x zu
Anwendungen
Die Rechtsregel kann für verschiedene physikalische Größen angewendet werden. Lassen Sie uns einige davon kennen:
Winkelgeschwindigkeit und Beschleunigung
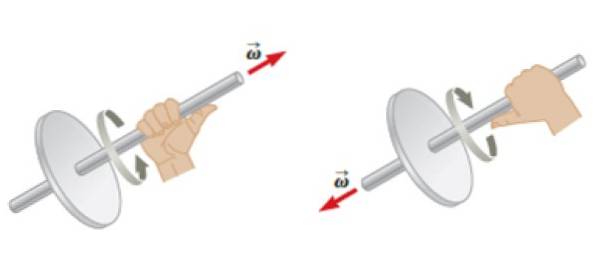
Beide Winkelgeschwindigkeit ω als Winkelbeschleunigung α Sie sind Vektoren. Wenn sich ein Objekt um eine feste Achse dreht, ist es möglich, die Richtung und den Sinn dieser Vektoren mithilfe der Rechtsregel zuzuweisen: Die vier Finger werden nach der Drehung gekräuselt, und der Daumen bietet sofort die Richtung und den Sinn der Winkelgeschwindigkeit an ω.
Die Winkelbeschleunigung seinerseits α wird die gleiche Adresse haben wie ω, aber seine Bedeutung hängt davon ab, ob ω nimmt mit der Zeit zu oder ab. Im ersten Fall haben beide die gleiche Richtung und den gleichen Sinn, im zweiten Fall haben sie entgegengesetzte Richtungen..
Drehimpuls
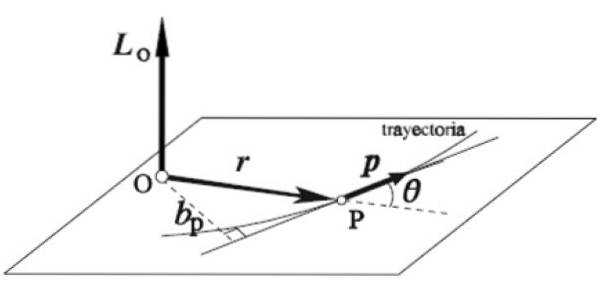
Der Drehimpulsvektor L.ODER eines Teilchens, das sich um eine bestimmte Achse O dreht, ist als das Vektorprodukt seines momentanen Positionsvektors definiert r und der lineare Impuls p::
L. = r x p
Die Regel der rechten Hand wird folgendermaßen angewendet: Der Zeigefinger wird in die gleiche Richtung und Richtung gelegt r, der Mittelfinger auf dem von p, beide auf einer horizontalen Ebene, wie in der Abbildung. Der Daumen wird automatisch vertikal nach oben gestreckt, um die Richtung und den Drehimpuls anzuzeigen L.ODER.
Ausbildung
- Übung 1
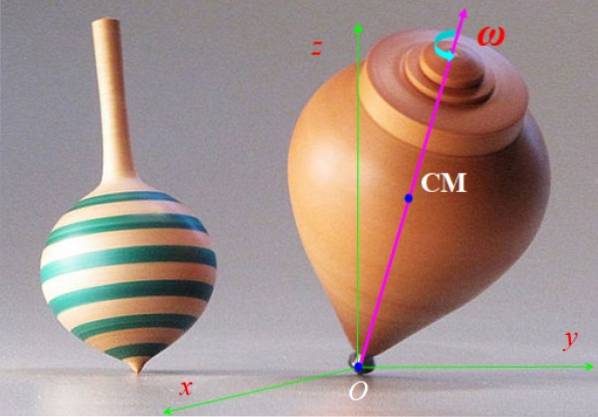
Das Oberteil in Abbildung 6 dreht sich schnell mit Winkelgeschwindigkeit ω und seine Symmetrieachse dreht sich langsamer um die vertikale Achse z. Diese Bewegung heißt Präzession. Beschreiben Sie die auf den Kreisel einwirkenden Kräfte und deren Wirkung.
Lösung
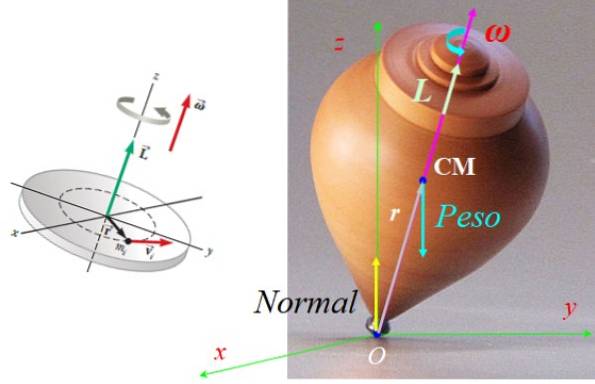
Die auf die Oberseite wirkenden Kräfte sind normal N., auf den Drehpunkt mit dem Boden O plus dem Gewicht M aufgetragenG, angewendet im Massenschwerpunkt CM, mit G der Beschleunigungsvektor der Schwerkraft, vertikal nach unten gerichtet (siehe Abbildung 7).
Beide Kräfte gleichen sich aus, daher bewegt sich die Oberseite nicht. Das Gewicht erzeugt jedoch ein Drehmoment oder Drehmoment τ netto in Bezug auf Punkt O, gegeben durch:
τODER = rODER x F., mit F = M.G.
Was r und MG Sie befinden sich immer in der gleichen Ebene, in der sich die Oberseite dreht, gemäß der rechten Regel das Drehmoment τODER befindet sich immer im Flugzeug xy, senkrecht zu beiden r Was G.
Beachten Sie, dass N. erzeugt kein Drehmoment in Bezug auf O, weil sein Vektor r in Bezug auf O ist null. Dieses Drehmoment erzeugt eine Änderung des Drehimpulses, die bewirkt, dass die Oberseite um die Z-Achse vorangeht..
- Übung 2
Geben Sie die Richtung und den Sinn des Drehimpulsvektors an L. von oben in Abbildung 6.
Lösung
Jeder Punkt oben hat die Masse mich, Geschwindigkeit vich und Positionsvektor rich, wenn es sich um die z-Achse dreht. Drehimpuls L.ich des Teilchens ist:
L.ich = rich x pich = rich x michvich
Angenommen rich Y. vich sind senkrecht, die Größe von L. es ist:
L.ich = michrichvich
Lineargeschwindigkeit v hängt mit der Winkelgeschwindigkeit zusammen ω durch:
vich = richω
Deshalb:
L.ich = michrich (richω) = michrichzweiω
Der Gesamtdrehimpuls des Kreisels L ist die Summe des Drehimpulses jedes Teilchens:
L = (∑michrichzwei ) ω
∑ michrichzwei ist der Trägheitsmoment I von oben, dann:
L.= Ichω
Deshalb L. Y. ω haben die gleiche Richtung und den gleichen Sinn wie in Abbildung 7 gezeigt.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Bedford, 2000. A. Technische Mechanik: Statik. Addison Wesley.
- Kirkpatrick, L. 2007. Physik: Ein Blick auf die Welt. 6. gekürzte Ausgabe. Lernen einbinden.
- Knight, R. 2017. Physik für Wissenschaftler und Ingenieure: ein strategischer Ansatz. Pearson.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1 und 2. 7 .. Ed. Lernen einbinden.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.