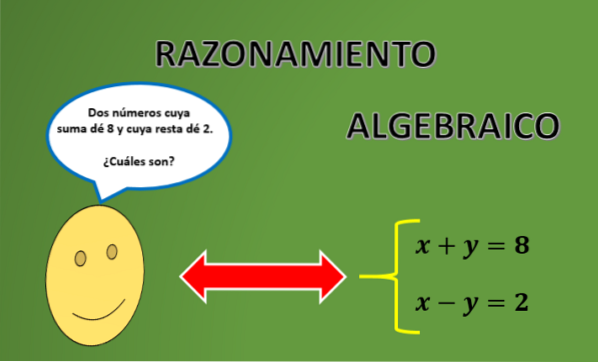
Das algebraisches Denken Es besteht im Wesentlichen darin, ein mathematisches Argument durch eine spezielle Sprache zu kommunizieren, was es strenger und allgemeiner macht und algebraische Variablen und Operationen verwendet, die untereinander definiert sind. Ein Merkmal der Mathematik ist die logische Strenge und abstrakte Tendenz, die in ihren Argumenten verwendet wird..
Dazu ist es notwendig, die richtige "Grammatik" zu kennen, die in diesem Schreiben verwendet werden soll. Darüber hinaus vermeidet algebraisches Denken Unklarheiten bei der Rechtfertigung eines mathematischen Arguments, was für den Nachweis eines mathematischen Ergebnisses unerlässlich ist..
Artikelverzeichnis
Eine algebraische Variable ist einfach eine Variable (ein Buchstabe oder ein Symbol), die ein bestimmtes mathematisches Objekt darstellt..
Beispielsweise werden die Buchstaben x, y, z häufig verwendet, um die Zahlen darzustellen, die eine gegebene Gleichung erfüllen; die Buchstaben p, q r, um Satzformeln darzustellen (oder ihre jeweiligen Großbuchstaben, um bestimmte Sätze darzustellen); und die Buchstaben A, B, X usw., um Mengen darzustellen.
Der Begriff "Variable" betont, dass das betreffende Objekt nicht fest ist, sondern variiert. Dies ist der Fall bei einer Gleichung, bei der Variablen verwendet werden, um im Prinzip unbekannte Lösungen zu bestimmen.
Im Allgemeinen kann eine algebraische Variable als Buchstabe betrachtet werden, der ein Objekt darstellt, unabhängig davon, ob es fest ist oder nicht..
So wie algebraische Variablen zur Darstellung mathematischer Objekte verwendet werden, können wir auch Symbole zur Darstellung mathematischer Operationen betrachten.
Beispielsweise steht das Symbol "+" für die Operation "Addition". Andere Beispiele sind die unterschiedlichen symbolischen Notationen logischer Verknüpfungen bei Sätzen und Mengen..
Ein algebraischer Ausdruck ist eine Kombination von algebraischen Variablen durch zuvor definierte Operationen. Beispiele hierfür sind die grundlegenden Operationen der Addition, Subtraktion, Multiplikation und Division zwischen Zahlen oder die logischen Verknüpfungen in Sätzen und Mengen..
Algebraisches Denken ist dafür verantwortlich, ein mathematisches Denken oder Argument durch algebraische Ausdrücke auszudrücken.
Diese Form des Ausdrucks hilft, das Schreiben zu vereinfachen und abzukürzen, da sie symbolische Notationen verwendet und ein besseres Verständnis des Denkens ermöglicht, indem es klarer und präziser dargestellt wird.
Schauen wir uns einige Beispiele an, die zeigen, wie algebraisches Denken verwendet wird. Es wird sehr regelmäßig verwendet, um Logik- und Argumentationsprobleme zu lösen, wie wir gleich sehen werden..
Betrachten Sie den bekannten mathematischen Satz "Die Summe zweier Zahlen ist kommutativ." Mal sehen, wie wir diesen Satz algebraisch ausdrücken können: Wenn zwei Zahlen "a" und "b" gegeben sind, bedeutet dieser Satz, dass a + b = b + a.
Die Argumentation, die verwendet wird, um den ursprünglichen Satz zu interpretieren und in algebraischen Begriffen auszudrücken, ist algebraisches Denken..
Wir könnten auch den berühmten Ausdruck "die Reihenfolge der Faktoren ändert das Produkt nicht" erwähnen, der sich auf die Tatsache bezieht, dass das Produkt zweier Zahlen auch kommutativ ist und algebraisch als axb = bxa ausgedrückt wird.
In ähnlicher Weise können (und werden) die assoziativen und verteilenden Eigenschaften für Addition und Produkt, in denen Subtraktion und Division enthalten sind, algebraisch ausgedrückt..
Diese Art des Denkens umfasst eine sehr breite Sprache und wird in vielen verschiedenen Kontexten verwendet. Je nach Fall ist es in diesen Kontexten erforderlich, Muster zu erkennen, Sätze zu interpretieren und ihren Ausdruck in algebraischen Begriffen zu verallgemeinern und zu formalisieren, um eine gültige und sequentielle Argumentation bereitzustellen..
Das Folgende sind einige logische Probleme, die wir mit algebraischem Denken lösen werden:
Was ist die Zahl, die, wenn man die Hälfte davon nimmt, gleich eins ist??
Um diese Art von Übung zu lösen, ist es sehr nützlich, den Wert, den wir bestimmen möchten, mithilfe einer Variablen darzustellen. In diesem Fall möchten wir eine Zahl finden, die, wenn wir die Hälfte davon nehmen, die Nummer eins ergibt. Bezeichnen wir die gesuchte Zahl mit x.
"Die Hälfte nehmen" von einer Zahl bedeutet, sie durch 2 zu teilen. Das Obige kann also algebraisch als x / 2 = 1 ausgedrückt werden, und das Problem läuft darauf hinaus, eine Gleichung zu lösen, die in diesem Fall linear und sehr einfach zu lösen ist. Wenn wir nach x auflösen, erhalten wir, dass die Lösung x = 2 ist.
Zusammenfassend ist 2 die Zahl, die bei Einnahme der Hälfte gleich 1 ist.
Wie viele Minuten bis Mitternacht, wenn vor 10 Minuten 5/3 von dem, was jetzt noch übrig ist?
Geben Sie mit "z" die Anzahl der Minuten bis Mitternacht an (jeder andere Buchstabe kann verwendet werden). Mit anderen Worten, im Moment gibt es "z" Minuten bis Mitternacht. Dies bedeutet, dass es vor 10 Minuten noch „z + 10“ Minuten bis Mitternacht gab, und dies entspricht 5/3 dessen, was jetzt fehlt. das heißt, (5/3) z.
Dann läuft das Problem darauf hinaus, die Gleichung z + 10 = (5/3) z zu lösen. Multipliziert man beide Seiten der Gleichheit mit 3, so erhält man die Gleichung 3z + 30 = 5z.
Wenn wir nun die Variable "z" auf einer Seite der Gleichheit gruppieren, erhalten wir 2z = 15, was impliziert, dass z = 15 ist.
Es ist also 15 Minuten vor Mitternacht.
In einem Stamm, der Tauschhandel praktiziert, gibt es diese Äquivalenzen:
- Ein Speer und eine Halskette werden gegen einen Schild ausgetauscht.
- Ein Speer entspricht einem Messer und einer Halskette.
- Zwei Schilde werden gegen drei Messereinheiten ausgetauscht.
Wie viele Halsketten entspricht ein Speer??
Sean:
Co = eine Halskette
L = ein Speer
E = ein Schild
Cu = ein Messer
Wir haben also folgende Beziehungen:
Co + L = E.
L = Co + Cu
2E = 3Cu
Das Problem besteht also darin, ein Gleichungssystem zu lösen. Obwohl es mehr Unbekannte als Gleichungen gibt, kann dieses System gelöst werden, da sie uns nicht nach einer bestimmten Lösung fragen, sondern nach einer der Variablen als Funktion einer anderen. Was wir tun müssen, ist "Co" ausschließlich in Bezug auf "L" auszudrücken.
Aus der zweiten Gleichung ergibt sich Cu = L - Co. Wenn wir die dritte Gleichung einsetzen, erhalten wir E = (3L - 3Co) / 2. Schließlich wird durch Einsetzen und Vereinfachen in die erste Gleichung erhalten, dass 5Co = L; Das heißt, ein Speer entspricht fünf Halsketten.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.