Was ist Lineargeschwindigkeit? (Mit Übungen gelöst)

Das Lineargeschwindigkeit es ist definiert als das, was unabhängig von seiner Form immer tangential zu dem Pfad ist, dem das Teilchen folgt. Wenn sich das Teilchen immer in einem geradlinigen Pfad bewegt, ist es kein Problem, sich vorzustellen, wie der Geschwindigkeitsvektor dieser geraden Linie folgt.

Im Allgemeinen wird die Bewegung jedoch auf einer beliebig geformten Kurve ausgeführt. Jeder Teil der Kurve kann so modelliert werden, als wäre er Teil eines Radiuskreises zu, was an jedem Punkt den eingeschlagenen Weg tangiert.

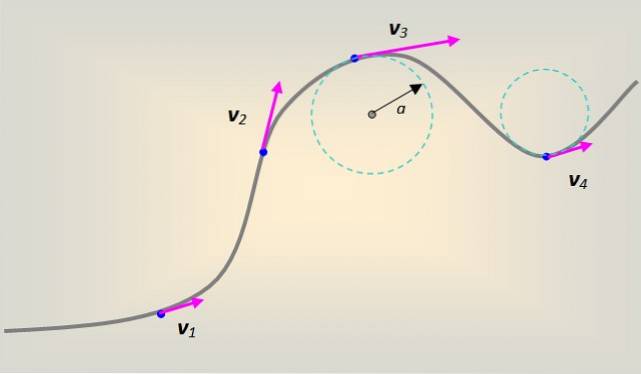
In diesem Fall begleitet die Lineargeschwindigkeit die Kurve tangential und jederzeit an jedem Punkt davon..

Mathematisch ist die momentane Lineargeschwindigkeit die Ableitung der Position in Bezug auf die Zeit. Sein r der Positionsvektor des Partikels zu einem Zeitpunkt t, dann ist die lineare Geschwindigkeit gegeben durch den Ausdruck:

v = r'(t) = dr / dt

Dies bedeutet, dass die lineare Geschwindigkeit oder Tangentialgeschwindigkeit, wie sie auch oft genannt wird, nichts anderes ist als die Änderung der Position in Bezug auf die Zeit..

Artikelverzeichnis

• 1 Lineargeschwindigkeit in Kreisbewegung
  • 1.1 Lineargeschwindigkeit, Winkelgeschwindigkeit und Zentripetalbeschleunigung
  • 1.2 - Gelöste Übung 1 
  • 1.3 - Gelöste Übung 2
• 2 Referenzen

Lineargeschwindigkeit in Kreisbewegung

Wenn sich die Bewegung auf einem Umfang befindet, können wir an jedem Punkt neben das Teilchen gehen und sehen, was in zwei ganz besonderen Richtungen geschieht: Eine davon ist diejenige, die immer in Richtung Zentrum zeigt. Das ist die Adresse radial.

Die andere wichtige Richtung ist die, die über den Umfang verläuft, dies ist die Richtung tangential und lineare Geschwindigkeit hat es immer.

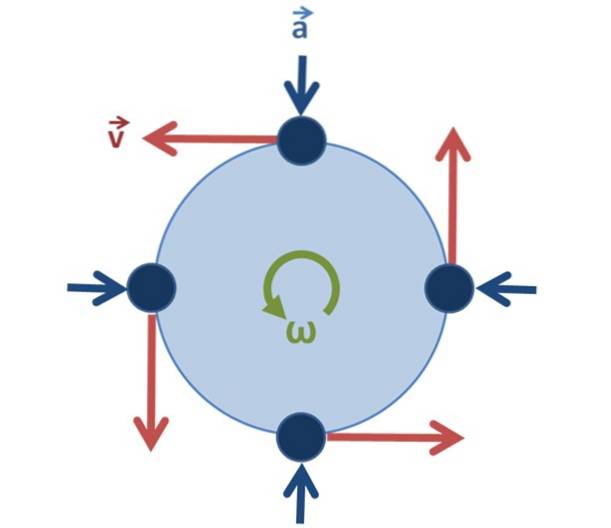
Im Falle einer gleichmäßigen Kreisbewegung ist es wichtig zu erkennen, dass die Geschwindigkeit nicht konstant ist, da der Vektor seine Richtung ändert, wenn sich das Teilchen dreht, aber sein Modul (die Größe des Vektors), der die Geschwindigkeit ist, bleibt ja unverändert.

Für diese Bewegung ist die Position als Funktion der Zeit gegeben durch s (t), wo s ist er Bogenlauf Y. t Es ist die Zeit. In diesem Fall ist die momentane Geschwindigkeit durch den Ausdruck gegeben v = ds / dt und es ist konstant.

Wenn sich auch die Größe der Geschwindigkeit ändert (wir wissen bereits, dass die Richtung immer stimmt, sonst könnte sich das Mobiltelefon nicht drehen), sehen wir uns einer unterschiedlichen Kreisbewegung gegenüber, bei der das Mobiltelefon zusätzlich zum Drehen bremsen oder beschleunigen kann.

Lineargeschwindigkeit, Winkelgeschwindigkeit und Zentripetalbeschleunigung

Die Bewegung des Teilchens kann auch aus der Sicht des gesehen werden überstrichener Winkel, anstatt es vom Torbogen aus zu tun. In einem solchen Fall sprechen wir von der Winkelgeschwindigkeit. Für eine Bewegung auf einem Radiusumfang R., Es gibt eine Beziehung zwischen Bogen (im Bogenmaß) und Winkel:

s = R & thgr;

Zeitliche Ableitung auf beiden Seiten:

ds / dt = R (d & thgr;/ dt)

Aufrufen der Ableitung von θ in Bezug auf t Was Winkelgeschwindigkeit und wenn wir es mit dem griechischen Buchstaben ω "Omega" bezeichnen, haben wir diese Beziehung:

v = ωR.

Zentripetalbeschleunigung

Alle Kreisbewegungen haben Zentripetalbeschleunigung, die immer auf die Mitte des Umfangs gerichtet ist. Sie stellt sicher, dass sich die Geschwindigkeit ändert, um sich mit dem Partikel zu bewegen, während es sich dreht.

Zentripetalbeschleunigung zu_c oder zu_R. zeigt immer zur Mitte (siehe Abbildung 2) und bezieht sich auf die Lineargeschwindigkeit wie folgt:

zu_c = v^zwei / R.

Und mit der Winkelgeschwindigkeit als:

zu_c = (ωR)^zwei / R = ω^zweiR.

Für eine gleichmäßige Kreisbewegung ist die Position s (t) ist von der Form:

s (t) = so + vt

Weiterhin muss die variierte Kreisbewegung eine Beschleunigungskomponente haben, die genannt wird tangentiale Beschleunigung zu_T., Hier geht es darum, die Größe der Lineargeschwindigkeit zu ändern. Ja zu_T.  es ist konstant, Die Position ist:

s (t) = s_oder + v_odert + ½ a_T.t^zwei

Mit v_oder als Anfangsgeschwindigkeit.

Gelöste Probleme der Lineargeschwindigkeit

Die gelösten Übungen helfen, die richtige Verwendung der oben angegebenen Konzepte und Gleichungen zu verdeutlichen..

-Gelöste Übung 1 

Ein Insekt bewegt sich auf einem Halbkreis mit einem Radius von R = 2 m, ausgehend von der Ruhe am Punkt A, während es seine lineare Geschwindigkeit mit einer Geschwindigkeit von p m / s erhöht^zwei. Finden Sie: a) Nach wie langer Zeit erreicht es Punkt B, b) den linearen Geschwindigkeitsvektor zu diesem Zeitpunkt, c) den Beschleunigungsvektor zu diesem Zeitpunkt.

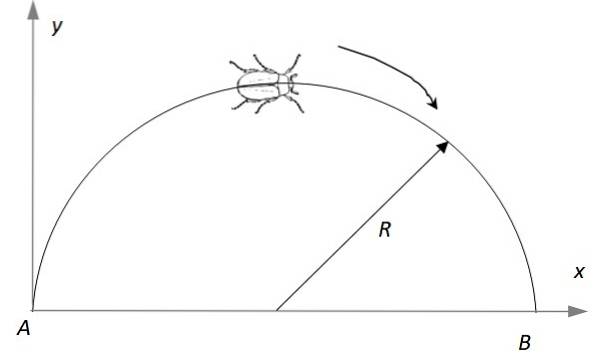
Lösung

a) Die Aussage zeigt an, dass die Tangentialbeschleunigung konstant ist und gleich π m / s ist^zwei, dann ist es gültig, die Gleichung für gleichmäßig variierte Bewegungen zu verwenden:

s (t) = s_oder + v_odert + ½ a_T..t^zwei

Mit s_oder = 0 und v_oder = 0:

s (t) = ½ a_T..t^zwei

s = πR. (Halbe Länge des Umfangs)

t = (2. πR. /.zu_T.) ^½ s = (2π.2 / π)^½s = 2 s

b) v (t) = v_oder + zu_T.. t = 2π Frau

Am Punkt B zeigt der lineare Geschwindigkeitsvektor in vertikaler Richtung nach unten in die Richtung (-Y.):

v (t) = 2π Frau((-Y.)

c) Wir haben bereits die Tangentialbeschleunigung, die Zentripetalbeschleunigung fehlt, um den Geschwindigkeitsvektor zu haben zu::

zu_c = v^zwei / R = (2π)^zwei / 2 m / s^zwei = 2π^zwei Frau^zwei

zu = a_c ((-x) + a_T. ((-Y.) = 2π^zwei((-x) + π ((-Y.) Frau^zwei

-Übung gelöst 2

Ein Teilchen dreht sich in einem Kreis mit einem Radius von 2,90 m. Zu einem bestimmten Zeitpunkt beträgt seine Beschleunigung 1,05 m / s^zwei in einer Richtung, in der es mit seiner Bewegungsrichtung 32º bildet. Finden Sie seine lineare Geschwindigkeit bei: a) diesem Moment, b) 2 Sekunden später, unter der Annahme, dass die tangentiale Beschleunigung konstant ist.

Lösung

a) Die Bewegungsrichtung ist genau die tangentiale Richtung:

zu_T. = 1,05 m / s^zwei . cos 32º = 0,89 m / s^zwei ;; zu_C. = 1,05 m / s^zwei . sin 32º = 0,56 m / s^zwei

Geschwindigkeit löscht sich von zu_c = v^zwei / R. Was:

v = (R.a._c)^1/2  = 1,27 m / s

b) Die folgende Gleichung gilt für gleichmäßig variierte Bewegungen: v = v_oder + zu_T.t = 1,27 + 0,89,2^zwei m / s = 4,83 m / s

Verweise

1. Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physikreihe für Naturwissenschaften und Technik. Band 3 .. Auflage. Kinematik. 199-232.
3. Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6^th… Ed Prentice Hall. 62-64.
4. Relativbewegung. Wiederhergestellt von: course.lumenlearning.com
5. Wilson, J. 2011. Physik 10. Pearson Education. 166-168.