
Was ist dynamisches Gleichgewicht? (Mit Beispiel)
Das dynamisches Gleichgewicht Dies ist der Zustand, in dem ein sich bewegendes Objekt idealerweise als Teilchen dargestellt wird, wenn seine Bewegung geradlinig gleichmäßig ist. Dieses Phänomen tritt auf, wenn die Summe der auf ihn einwirkenden äußeren Kräfte aufgehoben wird..
Es wird oft angenommen, dass Ruhe die einzig mögliche Folge ist, wenn auf ein Objekt keine Netto- oder resultierende Kraft ausgeübt wird. Oder auch, damit ein Körper im Gleichgewicht ist, darf keine Kraft wirken.
-

Abbildung 1. Diese Katze bewegt sich im dynamischen Gleichgewicht, wenn sie sich mit konstanter Geschwindigkeit bewegt. Quelle: Pixabay.
In der Realität ist das Gleichgewicht das Fehlen einer Beschleunigung, und daher ist eine konstante Geschwindigkeit durchaus möglich. Die Katze in der Figur kann sich ohne Beschleunigung bewegen.
Ein Objekt mit gleichmäßiger Kreisbewegung befindet sich nicht im dynamischen Gleichgewicht. Obwohl seine Geschwindigkeit konstant ist, gibt es eine Beschleunigung, die auf die Mitte des Umfangs gerichtet ist und ihn auf dem Weg hält. Diese Beschleunigung ist dafür verantwortlich, den Geschwindigkeitsvektor entsprechend zu ändern.
Die Nullgeschwindigkeit ist eine besondere Situation des Gleichgewichts eines Teilchens, die der Bestätigung entspricht, dass sich das Objekt in Ruhe befindet.
Die Betrachtung von Objekten als Partikel ist eine sehr nützliche Idealisierung bei der Beschreibung ihrer globalen Bewegung. In Wirklichkeit bestehen die sich bewegenden Objekte, die uns umgeben, aus einer großen Anzahl von Partikeln, deren individuelles Studium umständlich wäre..
Artikelverzeichnis
- 1 Das Prinzip der Überlagerung
- 2 Rotations- und Gleichgewichtsbedingungen
- 2.1 Drehmoment oder Moment einer Kraft
- 2.2 Gleichgewichtsbedingungen für ein erweitertes Objekt
- 2.3 Lösung
- 3 Referenzen
Das Prinzip der Überlagerung
Dieses Prinzip ermöglicht es, die Wirkung mehrerer Kräfte auf ein Objekt durch ein Äquivalent zu ersetzen, das als resultierende Kraft FR oder Nettokraft FN bezeichnet wird und in diesem Fall Null ist:
F1 + F2 + F3 +…. = FR = 0
Wo die Kräfte F1, F2, F3 ..., Fi die verschiedenen Kräfte sind, die auf den Körper wirken. Die Summationsnotation ist eine kompakte Ausdrucksweise:
Solange keine unausgeglichene Kraft eingreift, kann sich das Objekt mit konstanter Geschwindigkeit unbegrenzt weiterbewegen, da nur eine Kraft dieses Panorama verändern kann.
In Bezug auf die Komponenten der resultierenden Kraft wird der Zustand des dynamischen Gleichgewichts eines Teilchens wie folgt ausgedrückt: Fx = 0; Fy = 0; Fz = 0.
Rotations- und Gleichgewichtsbedingungen
Für das Partikelmodell ist die Bedingung FR = 0 eine ausreichende Garantie für das Gleichgewicht. Unter Berücksichtigung der Abmessungen des untersuchten Mobiltelefons besteht jedoch die Möglichkeit, dass sich das Objekt drehen kann.
Die Drehbewegung impliziert das Vorhandensein einer Beschleunigung, daher befinden sich die rotierenden Körper nicht im dynamischen Gleichgewicht. Das Drehen eines Körpers erfordert nicht nur die Teilnahme einer Kraft, sondern es ist notwendig, sie an der geeigneten Stelle anzuwenden.
Um dies zu überprüfen, kann ein dünner Stab in der Länge auf eine reibungsfreie Oberfläche wie eine gefrorene Oberfläche oder einen hochglanzpolierten Spiegel oder Glas gelegt werden. Die Normale gleicht das Gewicht vertikal aus, und durch horizontales Aufbringen von zwei Kräften F1 und F2 gleicher Größe gemäß dem Diagramm in der folgenden Abbildung wird überprüft, was passiert:
-
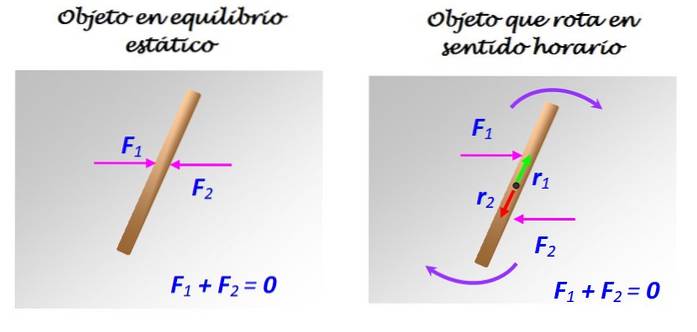
Abbildung 2. Ein Stab auf einer reibungsfreien Oberfläche kann sich im Gleichgewicht befinden oder nicht, je nachdem, wie die Kräfte 1 und 2 angewendet werden. Quelle: Eigene Ausarbeitung.
Wenn F1 und F2 wie links gezeigt mit einer gemeinsamen Wirkungslinie angewendet werden, bleibt die Stange in Ruhe. Wenn jedoch F1 und F2 wie rechts gezeigt angewendet werden, mit unterschiedlichen Wirkungslinien, obwohl parallel, tritt eine Drehung im Uhrzeigersinn um die Achse auf, die durch die Mitte verläuft.
In diesem Fall bilden F1 und F2 ein paar Kräfte oder einfach ein Paar.
Drehmoment oder Moment einer Kraft
Die Wirkung des Drehmoments besteht darin, eine Drehung auf ein verlängertes Objekt wie die Stange im Beispiel zu erzeugen. Die geladene Vektorgröße wird als Drehmoment oder auch als Moment einer Kraft bezeichnet. Es wird als τ bezeichnet und berechnet durch:
τ = r x F.
In diesem Ausdruck ist F die aufgebrachte Kraft und r der Vektor, der von der Drehachse zum Aufbringungspunkt der Kraft geht (siehe Abbildung 2). Die Richtung von τ ist immer senkrecht zu der Ebene, in der F und r liegen, und ihre Einheiten im internationalen System sind Nm.
Zum Beispiel ist die Richtung der von F1 und F2 erzeugten Momente gemäß den Regeln des Vektorprodukts zum Papier gerichtet.
Obwohl sich die Kräfte gegenseitig aufheben, tun dies ihre Drehmomente nicht. Das Ergebnis ist die angezeigte Drehung.
Gleichgewichtsbedingungen für ein erweitertes Objekt
Es gibt zwei Bedingungen, die erfüllt sein müssen, um das Gleichgewicht eines erweiterten Objekts zu gewährleisten:
Es gibt eine Box oder einen Kofferraum mit einem Gewicht von 16 kg-f, die mit konstanter Geschwindigkeit über eine schiefe Ebene gleiten. Der Neigungswinkel des Keils beträgt θ = 36º. Antworten:
a) Wie groß ist die dynamische Reibungskraft, die erforderlich ist, damit der Kofferraum mit konstanter Geschwindigkeit gleiten kann??
b) Wie hoch ist der kinetische Reibungskoeffizient??
c) Wenn die Höhe h der schiefen Ebene 3 Meter beträgt, ermitteln Sie die Abstiegsgeschwindigkeit des Rumpfes in dem Wissen, dass es 4 Sekunden dauert, bis der Boden erreicht ist.
Lösung
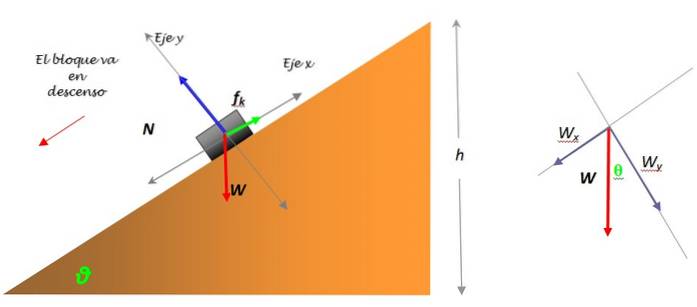
Der Stamm kann wie ein Partikel behandelt werden. Aus diesem Grund werden die Kräfte an einem Punkt angewendet, der sich ungefähr in seiner Mitte befindet und an dem angenommen werden kann, dass sich seine gesamte Masse konzentriert. An diesem Punkt werden Sie verfolgt.
-

Abbildung 3. Freikörperdiagramm für bergab gleitenden Kofferraum und Gewichtsverteilung (rechts). Quelle: selbst gemacht.
Das Gewicht W ist die einzige Kraft, die nicht auf eine der Koordinatenachsen fällt und in zwei Komponenten zerlegt werden muss: Wx und Wy. Diese Zerlegung ist im Diagramm dargestellt (Abbildung 3).
Es ist auch bequem, das Gewicht auf Einheiten des internationalen Systems zu übertragen, für die es ausreicht, mit 9,8 zu multiplizieren:
Wy = W. cos & thgr; = 16 × 9,8 × cos 36 ° N = 126,9 N.
Wx = W. sinθ = 16 x 9,8 x sin 36º = 92,2 N.
Absatz a
Entlang der horizontalen Achse befinden sich die horizontale Komponente des Gewichts Wx und die dynamische oder kinetische Reibungskraft fk, die der Bewegung entgegenwirkt.
Durch Auswahl der positiven Richtung in Bewegungsrichtung ist leicht zu erkennen, dass Wx für den Block verantwortlich ist, der bergab geht. Und da die Reibung entgegengesetzt ist, anstatt zu rutschen, hat der Block die Möglichkeit, mit konstanter Geschwindigkeit bergab zu gleiten.
Die erste Gleichgewichtsbedingung ist ausreichend, da wir den Stamm als Partikel behandeln, was uns in der Aussage versichert wird, dass er sich im dynamischen Gleichgewicht befindet:
Wx - fk = 0 (keine Beschleunigung in horizontaler Richtung)
fk = 92,2 N.
Abschnitt b
Die Größe der dynamischen Reibung ist konstant und ist gegeben durch fk = μk N. Dies bedeutet, dass die dynamische Reibungskraft proportional zur Normalen ist und deren Größe erforderlich ist, um den Reibungskoeffizienten zu kennen.
Wenn man das Freikörperdiagramm betrachtet, kann man sehen, dass wir auf der vertikalen Achse die Normalkraft N haben, die der Keil auf den Rumpf ausübt und nach oben gerichtet ist. Sie ist mit der vertikalen Komponente des Gewichts Wy ausgeglichen. Die Auswahl als positiver Sinn und die Verwendung des zweiten Newtonschen Gesetzes und der Gleichgewichtsbedingung ergibt:
N - Wy = 0 (es gibt keine Bewegung entlang der vertikalen Achse)
Deshalb:
N = Wy = 126,9 N.
fk = μk N.
μk = fk / N = 92,2 / 126,9 = 0,73
Abschnitt c
Die Gesamtstrecke, die der Stamm von der Spitze des Keils bis zum Boden zurücklegt, wird durch Trigonometrie ermittelt:
d = h / sin 36º = 3 / sin 36º m = 5,1 m.
Zur Berechnung der Geschwindigkeit wird die Definition für eine gleichmäßige geradlinige Bewegung verwendet:
v = d / t = 5,1 m / 4 s = 1,3 m / s
Verweise
- Rex, A. 2011. Grundlagen der Physik. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Ed. Lernen einbinden. 120 - 124.
- Serway, R., Vulle, C. 2011. Grundlagen der Physik. 9. Aufl. Lernen einbinden. 99-112.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Physik. Addison Wesley. 148-164.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.