
Wie ist das Gleichgewicht des Partikels? (Mit Beispielen)
Das Teilchengleichgewicht Es ist ein Zustand, in dem ein Teilchen gefunden wird, wenn die äußeren Kräfte, die auf sie wirken, sich gegenseitig aufheben. Dies setzt voraus, dass es einen konstanten Zustand beibehält, so dass es je nach spezifischer Situation auf zwei verschiedene Arten auftreten kann.
Das erste ist, sich im statischen Gleichgewicht zu befinden, in dem das Teilchen unbeweglich ist; und das zweite ist das dynamische Gleichgewicht, bei dem sich die Summe der Kräfte aufhebt, das Teilchen jedoch eine gleichmäßige geradlinige Bewegung aufweist.

Das Partikelmodell ist eine sehr nützliche Annäherung, um die Bewegung eines Körpers zu untersuchen. Es besteht in der Annahme, dass die gesamte Körpermasse unabhängig von der Größe des Objekts auf einen einzigen Punkt konzentriert ist. Auf diese Weise können Sie einen Planeten, ein Auto, ein Elektron oder eine Billardkugel darstellen.
Artikelverzeichnis
- 1 Die resultierende Kraft
- 2 Freikörperdiagramme
- 3 Möglichkeiten, die Gleichgewichtsbedingung anzuwenden
- 3.1 Zwei Kräfte gleicher Größe und entgegengesetzter Richtung und Richtungen
- 3.2 Zwei Kräfte unterschiedlicher Größe, gleiche Richtung und entgegengesetzte Richtung
- 3.3 Zwei Kräfte gleicher Größe und unterschiedlicher Richtung
- 3.4 Drei Kräfte mit unterschiedlicher Richtung
- 4 Reibung
- 4.1 Die dynamische Reibung
- 5 Arbeitsbeispiel
- 5.1 Lösung
- 6 Referenzen
Die resultierende Kraft
Der Punkt, der das Objekt darstellt, ist der Ort, an dem die Kräfte wirken, die es beeinflussen. Alle diese Kräfte können durch eine einzige ersetzt werden, die den gleichen Effekt hat, der als bezeichnet wird resultierende Kraft oder Nettokraft und wird als F bezeichnetR. oder F.N..
Nach dem zweiten Newtonschen Gesetz erfährt der Körper bei einer unausgeglichenen resultierenden Kraft eine Beschleunigung proportional zur Kraft:
F.R. = m.a.
Wo zu ist die Beschleunigung, die das Objekt dank der Wirkung der Kraft und erhält m ist die Masse des Objekts. Was passiert, wenn der Körper nicht beschleunigt wird? Genau das, was zu Beginn angezeigt wurde: Der Körper ist in Ruhe oder bewegt sich mit gleichmäßiger geradliniger Bewegung, der es an Beschleunigung mangelt.
Für ein Teilchen im Gleichgewicht gilt Folgendes:
F.R. = 0
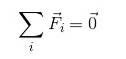
Da das Hinzufügen von Vektoren nicht unbedingt das Hinzufügen der Module bedeutet, müssen die Vektoren zerlegt werden. Somit gilt es auszudrücken:
F.x = m.a.x = 0; F.Y. = m.a.Y. = 0; F.z = m.a.z = 0
Freikörperdiagramme
Um die auf das Partikel einwirkenden Kräfte zu visualisieren, ist es zweckmäßig, ein Freikörperdiagramm zu erstellen, in dem alle auf das Objekt einwirkenden Kräfte durch Pfeile dargestellt werden..
Die obigen Gleichungen sind vektorischer Natur. Bei der Zerlegung der Kräfte werden sie durch Zeichen unterschieden. Auf diese Weise ist es möglich, dass die Summe seiner Komponenten Null ist.
Die folgenden Richtlinien sind wichtig, um die Zeichnung nützlich zu machen:
- Wählen Sie ein Referenzsystem, in dem sich die meisten Kräfte auf den Koordinatenachsen befinden.
- Das Gewicht wird immer senkrecht nach unten gezogen.
- Bei zwei oder mehr sich berührenden Oberflächen treten Normalkräfte auf, die immer durch Drücken des Körpers und senkrecht zu der Oberfläche, die ihn ausübt, gezogen werden..
- Bei einem Partikel im Gleichgewicht kann es zu Reibungen parallel zur Kontaktfläche kommen, die der möglichen Bewegung entgegenwirken, wenn das Partikel in Ruhe betrachtet wird, oder definitiv im Gegensatz, wenn sich das Partikel mit MRU bewegt (gleichmäßige geradlinige Bewegung)..
- Wenn es ein Seil gibt, wird die Spannung immer entlang gezogen und zieht den Körper.
Möglichkeiten, die Gleichgewichtsbedingung anzuwenden
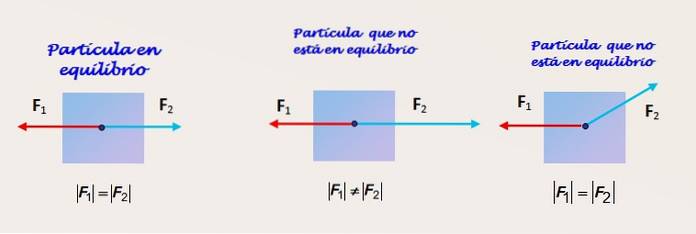
Zwei Kräfte gleicher Größe und entgegengesetzter Richtung und Richtungen
Abbildung 2 zeigt ein Partikel, auf das zwei Kräfte wirken. In der Abbildung links erhält das Teilchen die Wirkung von zwei Kräften F.1 und F.zwei die die gleiche Größe haben und in die gleiche Richtung und in entgegengesetzte Richtungen wirken.
Das Teilchen befindet sich im Gleichgewicht, aber mit den gelieferten Informationen ist es nicht möglich zu wissen, ob das Gleichgewicht statisch oder dynamisch ist. Weitere Informationen über den Trägheitsreferenzrahmen, von dem aus das Objekt beobachtet wird, sind erforderlich.
Zwei Kräfte unterschiedlicher Größe, gleiche Richtung und entgegengesetzte Richtungen
Die Figur in der Mitte zeigt das gleiche Teilchen, das diesmal nicht im Gleichgewicht ist, da die Größe der Kraft F.zwei ist größer als das von F.1. Daher gibt es eine unausgeglichene Kraft und das Objekt hat eine Beschleunigung in der gleichen Richtung wie F.zwei.
Zwei Kräfte gleicher Größe und unterschiedlicher Richtung
Schließlich sehen wir in der Abbildung rechts einen Körper, der sich ebenfalls nicht im Gleichgewicht befindet. Trotz der Tatsache, dass F.1 und F.zwei haben die gleiche Größe, die Kraft F.zwei ist nicht in der gleichen Richtung wie 1. Die vertikale Komponente von F.zwei wird von keinem anderen entgegengewirkt und das Teilchen erfährt eine Beschleunigung in diese Richtung.
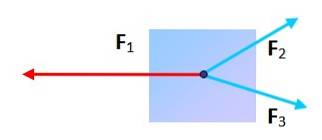
Drei Kräfte mit unterschiedlicher Richtung
Kann ein Teilchen, das drei Kräften ausgesetzt ist, im Gleichgewicht sein? Ja, solange beim Platzieren des Endes und des Endes eines jeden die resultierende Figur ein Dreieck ist. In diesem Fall ist die Vektorsumme Null.
Reibung
Eine Kraft, die häufig in das Gleichgewicht des Partikels eingreift, ist die Haftreibung. Es ist auf die Wechselwirkung des durch das Teilchen dargestellten Objekts mit der Oberfläche eines anderen zurückzuführen. Beispielsweise wird ein Buch im statischen Gleichgewicht auf einem geneigten Tisch als Partikel modelliert und verfügt über ein Freikörperdiagramm wie das folgende:
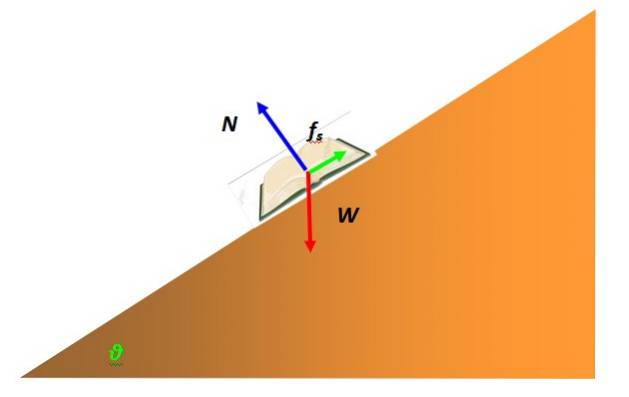
Die Kraft, die verhindert, dass das Buch über die Oberfläche der schiefen Ebene gleitet und in Ruhe bleibt, ist Haftreibung. Dies hängt von der Art der Kontaktflächen ab, die mikroskopisch eine Rauheit mit Spitzen aufweisen, die miteinander ineinander greifen und die Bewegung erschweren..
Der Maximalwert der Haftreibung ist proportional zur Normalkraft, der Kraft, die von der Oberfläche auf das getragene Objekt ausgeübt wird, jedoch senkrecht zu dieser Oberfläche. Im Beispiel im Buch ist es blau angezeigt. Mathematisch wird es so ausgedrückt:
F.s mehr∝ N.
Die Proportionalitätskonstante ist die Haftreibungskoeffizient μs, die experimentell bestimmt wird, ist dimensionslos und hängt von der Art der Kontaktflächen ab.
F.s max = μs N.
Die dynamische Reibung
Befindet sich ein Teilchen im dynamischen Gleichgewicht, findet bereits eine Bewegung statt und es tritt keine statische Reibung mehr ein. Wenn eine Reibungskraft vorhanden ist, die der Bewegung entgegenwirkt, wirkt die dynamische Reibung, deren Größe konstant ist und gegeben ist durch:
F.k = μk N.
Wo μk ist er dynamischer Reibungskoeffizient, Dies hängt auch von der Art der Kontaktflächen ab. Wie der Haftreibungskoeffizient ist er dimensionslos und sein Wert wird experimentell bestimmt.
Der Wert des dynamischen Reibungskoeffizienten ist normalerweise geringer als der der Haftreibung.
Gearbeitetes Beispiel
Das Buch in Abbildung 3 befindet sich in Ruhe und hat eine Masse von 1,30 kg. Das Flugzeug hat einen Neigungswinkel von 30º. Finden Sie den Haftreibungskoeffizienten zwischen dem Buch und der ebenen Fläche.
Lösung
Es ist wichtig, ein geeignetes Referenzsystem auszuwählen, siehe folgende Abbildung:
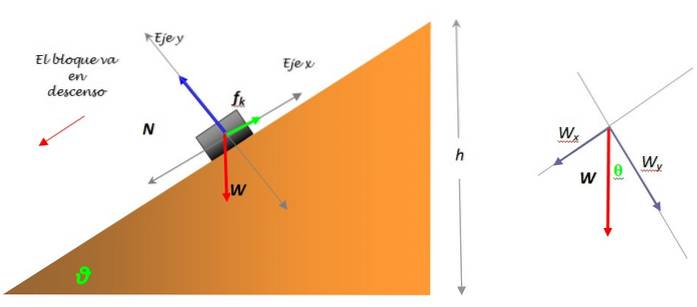
Das Gewicht des Buches hat Größe W = mg, Es ist jedoch notwendig, es in zwei Komponenten zu zerlegen: W.x Y. W.Y., da es die einzige Kraft ist, die nicht direkt über eine der Koordinatenachsen fällt. Die Zersetzung des Gewichts ist in der Abbildung links zu sehen.
W.Y. = mg · cos & thgr; = 1,30 × 9,8 × cos 30 ° N = 11,03 N.
W.x = mg sinθ = 1,30 x 9,8 x sin 30º = 6,37 N.
Die 2. Das Newtonsche Gesetz für die vertikale Achse lautet:
N - Wy = 0
N = mg. cos θ = 11,03 N..
Anwenden des 2 .. Newtonsches Gesetz für die x-Achse, wobei die Richtung der möglichen Bewegung als positiv gewählt wird:
W.x - F.s = 0
Die maximale Reibung beträgt F.s max= μsN., So:
W.x - μsN = 0
μs = W.x / N = 6,37 / 11,03 = 0,58
Verweise
- Rex, A. 2011. Grundlagen der Physik. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7ma. Ed. Lernen einbinden. 120 - 124.
- Serway, R., Vulle, C. 2011. Grundlagen der Physik. 9n / A Ed. Lernen einbinden. 99-112.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Physik. Addison Wesley. 148-164.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.