Das eindimensionale Wellen Sie sind solche, die sich in einer einzigen Richtung ausbreiten, unabhängig davon, ob die Schwingung in derselben Ausbreitungsrichtung auftritt oder nicht. Ein gutes Beispiel dafür ist die Welle, die sich wie eine Gitarre durch eine gespannte Saite bewegt..
In einer flachen Welle Kreuz, Die Partikel schwingen in vertikaler Richtung (sie gehen auf und ab, siehe den roten Pfeil in Abbildung 1), aber sie sind eindimensional, da sich die Störung nur in eine Richtung nach dem gelben Pfeil bewegt.
Eindimensionale Wellen treten im Alltag häufig auf. Der folgende Abschnitt beschreibt einige Beispiele von ihnen und auch von Wellen, die nicht eindimensional sind, um die Unterschiede klar zu bestimmen.
Artikelverzeichnis
Hier sind einige Beispiele für eindimensionale Wellen, die leicht beobachtet werden können:
- Ein Schallimpuls, der sich durch einen geraden Balken bewegt, da es sich um eine Störung handelt, die sich über die gesamte Länge des Balkens ausbreitet.
- Eine Welle, die sich durch einen Wasserkanal bewegt, obwohl die Verschiebung der Wasseroberfläche nicht parallel zum Kanal verläuft.
- Wellen, die sich auf einer Oberfläche oder durch einen dreidimensionalen Raum ausbreiten, können auch eindimensional sein, solange ihre Wellenfronten Ebenen parallel zueinander sind und sich nur in eine Richtung bewegen..
Ein Beispiel für eine nicht eindimensionale Welle sind Wellen, die sich auf einer stillen Wasseroberfläche bilden, wenn ein Stein fallen gelassen wird. Es ist eine zweidimensionale Welle mit einer zylindrischen Wellenfront.
Ein weiteres Beispiel für eine nicht eindimensionale Welle ist die Schallwelle, die ein Kracher erzeugt, indem er in einer bestimmten Höhe explodiert. Dies ist eine dreidimensionale Welle mit sphärischen Wellenfronten.
Der allgemeinste Weg, um eine eindimensionale Welle auszudrücken, die sich ohne Dämpfung in der positiven Richtung der Achse ausbreitet x und mit Geschwindigkeit v ist mathematisch:
y (x, t) = f (x - v.t)
In diesem Ausdruck Y. repräsentiert die Störung in der Position x Sofort t. Die Form der Welle ist durch die Funktion gegeben F.. Die in Abbildung 1 gezeigte Wellenfunktion lautet beispielsweise: y (x, t) = cos (x - v t) und das Wellenbild entspricht dem Moment t = 0.
Eine Welle wie diese, die durch eine Kosinus- oder Sinusfunktion beschrieben wird, wird aufgerufen harmonische Welle. Obwohl es nicht die einzige Wellenform ist, die existiert, ist sie von größter Bedeutung, da jede andere Welle als Überlagerung oder Summe harmonischer Wellen dargestellt werden kann. Es geht um das Bekannte Fourier-Theorem, so verwendet, um Signale aller Art zu beschreiben.
Wenn sich die Welle in die negative Richtung der x-Achse bewegt, ändert sie sich einfach v zum -v im Streit verlassen:
y (x, t) = g (x + v t)
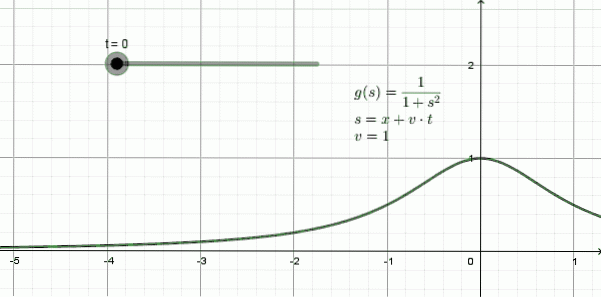
Abbildung 3 zeigt die Animation einer Welle, die sich nach links bewegt: Es handelt sich um eine Form, die als Funktion bezeichnet wird Lorentziana und sie mathematischer Ausdruck ist:
y (x, t) = 1 / (1 + (x + 1)⋅t)zwei
In diesem Beispiel ist die Ausbreitungsgeschwindigkeit v = 1, -eine Raumeinheit für jede Zeiteinheit-.
Die Wellengleichung ist eine partielle Ableitungsgleichung, deren Lösung natürlich eine Welle ist. Es stellt die mathematische Beziehung zwischen dem räumlichen Teil und dem zeitlichen Teil her und hat die Form:
Das Folgende ist der allgemeine Ausdruck y (x, t) für eine harmonische Welle:
y (x, t) = A.⋅cos (k⋅x ± ω⋅t + θo)
a) Beschreiben Sie die physikalische Bedeutung der Parameter A, k, ω Y. θo.
b) Welche Bedeutung haben die ± -Zeichen im Kosinusargument??
c) Stellen Sie sicher, dass der angegebene Ausdruck tatsächlich die Lösung der Wellengleichung aus dem vorherigen Abschnitt ist, und ermitteln Sie die Geschwindigkeit v Vermehrung.
Die Eigenschaften der Welle finden sich in folgenden Parametern:
-ZU repräsentiert die Amplitude oder "Wellenhöhe".
-was ist in Wellenzahl und hängt mit der Wellenlänge zusammen λ durch k = 2π / λ.
-ω ist das fWinkelfrequenz und ist verwandt mit dem Zeitraum T. Wellenschwingung durch
ω = 2π / T..
-θo ist der Anfangsphase, was mit dem Startpunkt der Welle zusammenhängt.
Ein negatives Vorzeichen wird genommen, wenn sich die Welle in die positive Richtung der X-Achse bewegt, andernfalls ein positives Vorzeichen..
Stellen Sie sicher, dass der angegebene Ausdruck eine einfache Lösung der Wellengleichung ist: Die partielle Ableitung der Funktion wird verwendet y (x, t) in Bezug auf x zweimal, teilweise in Bezug auf t zweimal neu abgeleitet, und dann beide Ergebnisse kombinieren, um eine Gleichheit zu erhalten:
Zweite Ableitung bezüglich x: ∂zweiy / ∂xzwei= -Kzwei. ZU⋅cos (k⋅x ± ω⋅t + θo)
Zweite Ableitung bezüglich t: ∂zweiy / ∂tzwei= -Ωzwei. ZU⋅cos (k⋅x ± ω⋅t + θo)
Diese Ergebnisse werden in der Wellengleichung eingesetzt:
-kzwei. ZU⋅cos (k⋅x ± ω⋅t + θo) = (1 / vzwei) (-ωzwei. ZU⋅cos (k⋅x ± ω⋅t + θo))
So viel ZU Da der Kosinus vereinfacht wird, da er auf beiden Seiten der Gleichheit erscheint und das Argument des Kosinus dasselbe ist, reduziert sich der Ausdruck auf:
-kzwei = (1 / vzwei) (-ωzwei)
Was erlaubt, eine Gleichung für zu erhalten v bezüglich ω Y. k::
vzwei = ωzwei / kzwei
v = ± ω / k
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.