
Ergänzende Winkel was sind sie, Berechnung, Beispiele, Übungen
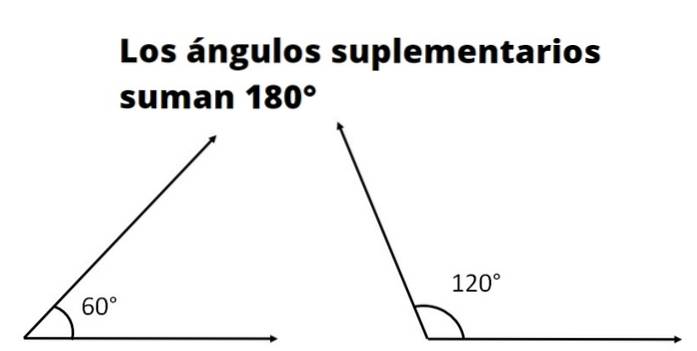
Zwei oder mehr sind Ergänzungswinkel wenn die Summe seiner Maße dem Maß eines geraden Winkels entspricht. Das Maß für einen geraden Winkel, auch ebener Winkel genannt, in Grad beträgt 180º und im Bogenmaß π.
Zum Beispiel stellen wir fest, dass die drei Innenwinkel eines Dreiecks sich ergänzen, da die Summe ihrer Maße 180º beträgt. In Abbildung 1 sind drei Winkel dargestellt. Aus dem Obigen folgt, dass α und β komplementär sind, da sie benachbart sind und ihre Summe einen geraden Winkel vervollständigt.
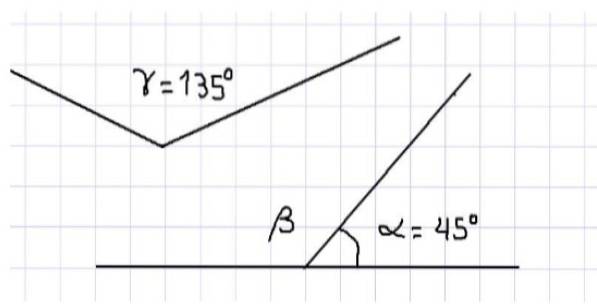
In derselben Figur haben wir auch die Winkel α und γ, die ebenfalls ergänzend sind, da die Summe ihrer Maße gleich dem Maß eines ebenen Winkels ist, dh 180º. Es kann nicht gesagt werden, dass die Winkel β und γ komplementär sind, da beide Winkel stumpf sind, ihre Maße größer als 90º sind und daher ihre Summe 180º überschreitet.
Andererseits kann festgestellt werden, dass das Maß des Winkels β gleich dem Maß des Winkels γ ist, da β = γ = 135º ist, wenn β zu α und γ zu α komplementär ist.
Artikelverzeichnis
- 1 Beispiele
- 1.1 Beispiel A.
- 1.2 Beispiel B.
- 1.3 Beispiel C.
- 1.4 Beispiel D.
- 1.5 Beispiel E.
- 1.6 Beispiel F.
- 2 Übungen
- 2.1 - Übung I.
- 2.2 - Übung II
- 2.3 - Übung III
- 3 Ergänzende Winkel in zwei Parallelen, die von einer Sekante geschnitten werden
- 3.1 - Übung IV
- 4 Referenzen
Beispiele
In den folgenden Beispielen wird darum gebeten, die unbekannten Winkel zu finden, die in Abbildung 2 mit Fragezeichen gekennzeichnet sind. Sie reichen von den einfachsten Beispielen bis zu einigen etwas ausführlicheren, bei denen der Leser vorsichtiger sein sollte.
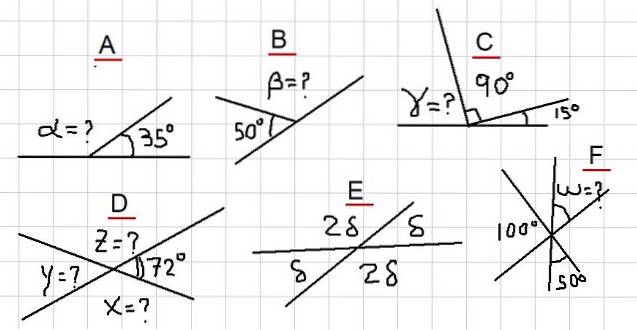
Beispiel A.
In der Abbildung haben wir, dass sich die benachbarten Winkel α und 35º zu einem ebenen Winkel addieren. Das heißt, α + 35º = 180º und daher ist es wahr, dass: α = 180º - 35º = 145º.
Beispiel B.
Da β mit dem Winkel von 50º komplementär ist, folgt, dass β = 180º - 50º = 130º ist.
Beispiel C.
Aus Fig. 2C ist die folgende Summe ersichtlich: γ + 90º + 15º = 180º. Das heißt, γ ist ergänzend mit dem Winkel 105º = 90º + 15º. Daraus wird geschlossen, dass:
γ = 180º - 105º = 75º
Beispiel D.
Da X zu 72º komplementär ist, folgt X = 180º - 72º = 108º. Außerdem ist Y zusätzlich zu X, also Y = 180º - 108º = 72º.
Und schließlich ist Z mit 72º ergänzend, daher ist Z = 180º - 72º = 108º.
Beispiel E.
Die Winkel δ und 2δ sind ergänzend, daher ist δ + 2δ = 180º. Was bedeutet, dass 3δ = 180º ist, und dies erlaubt uns wiederum zu schreiben: δ = 180º / 3 = 60º.
Beispiel F.
Wenn wir den Winkel zwischen 100º und 50º U nennen, dann ist U eine Ergänzung zu ihnen, weil beobachtet wird, dass ihre Summe einen ebenen Winkel vervollständigt.
Daraus folgt sofort, dass U = 150º. Da U durch den Scheitelpunkt zu W entgegengesetzt ist, ist W = U = 150º.
Ausbildung
Im Folgenden werden drei Übungen vorgeschlagen, bei denen der Wert der Winkel A und B in Grad ermittelt werden muss, damit die in Abbildung 3 gezeigten Beziehungen erfüllt sind. Bei der Lösung aller Übungen wird das Konzept der zusätzlichen Winkel verwendet..
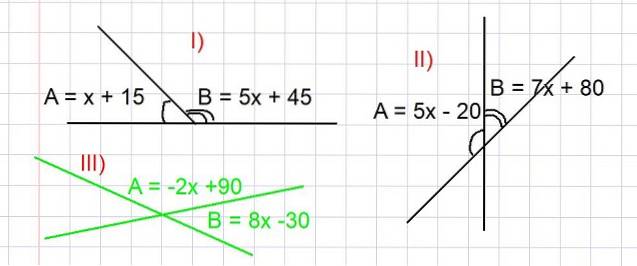
- Übung I.
Bestimmen Sie die Werte der Winkel A und B aus Teil I) von Abbildung 3.
Lösung
A und B sind ergänzend, woraus wir haben, dass A + B = 180 Grad ist, dann wird der Ausdruck von A und B als Funktion von x ersetzt, wie es im Bild erscheint:
(x + 15) + (5x + 45) = 180
Eine lineare Gleichung erster Ordnung wird erhalten. Um es zu lösen, werden die Begriffe sofort gruppiert:
6 x + 60 = 180
Wenn wir beide Mitglieder durch 6 teilen, haben wir:
x + 10 = 30
Und schließlich folgt, dass x 20º wert ist.
Jetzt müssen wir den Wert von x einstecken, um die angeforderten Winkel zu finden. Daher ist der Winkel A: A = 20 + 15 = 35º.
Und seinerseits ist der Winkel B B = 5 · 20 + 45 = 145º.
- Übung II
Finden Sie die Werte der Winkel A und B aus Teil II) von Abbildung 3.
Lösung
Da A und B zusätzliche Winkel sind, haben wir A + B = 180 Grad. Wenn wir den Ausdruck für A und B als Funktion von x ersetzen, der in Teil II) von 3 angegeben ist, haben wir:
(-2x + 90) + (8x - 30) = 180
Wiederum wird eine Gleichung ersten Grades erhalten, für die die Begriffe bequem gruppiert werden müssen:
6 x + 60 = 180
Wenn wir beide Mitglieder durch 6 teilen, haben wir:
x + 10 = 30
Daraus folgt, dass x 20º wert ist.
Mit anderen Worten ist der Winkel A = -2 · 20 + 90 = 50º. Während Winkel B = 8 * 20 - 30 = 130º.
- Übung III
Bestimmen Sie die Werte der Winkel A und B aus Teil III) von Abbildung 3 (in grüner Farbe)..
Lösung
Da A und B zusätzliche Winkel sind, haben wir A + B = 180 Grad. Wir müssen den Ausdruck für A und B als Funktion von x in Abbildung 3 ersetzen, aus dem wir haben:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Wenn wir beide Mitglieder durch 12 teilen, um den Wert von x zu ermitteln, haben wir:
x + 5 = 15
Schließlich wird festgestellt, dass x 10 Grad wert ist.
Nun fahren wir mit dem Ersatz fort, um den Winkel A zu finden: A = 5 * 10 -20 = 30º. Und für Winkel B: B = 7 * 10 + 80 = 150º
Ergänzende Winkel in zwei Parallelen, geschnitten von einer Sekante
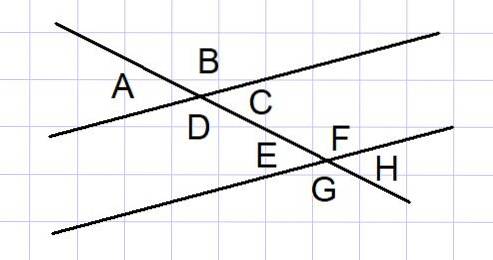
Zwei parallele Linien, die von einer Sekante geschnitten werden, sind bei einigen Problemen eine übliche geometrische Konstruktion. Zwischen solchen Linien werden 8 Winkel gebildet, wie in 4 gezeigt.
Von diesen 8 Winkeln sind einige Winkelpaare ergänzend, die wir unten auflisten:
- Die Außenwinkel A und B und die Außenwinkel G und H.
- Die Innenwinkel D und C und die Innenwinkel E und F.
- Die Außenwinkel A und G und die Außenwinkel B und H.
- Die Innenwinkel D und E sowie die Innenwinkel C und F.
Der Vollständigkeit halber werden auch die einander gleichen Winkel genannt:
- Die internen Alternativen: D = F und C = E.
- Das Äußere wechselt: A = H und B = G.
- Die entsprechenden: A = E und C = H.
- Gegensätze durch Scheitelpunkt A = C und E = H.
- Die entsprechenden: B = F und D = G.
- Gegensätze durch Scheitelpunkt B = D und F = G.
- Übung IV
Unter Bezugnahme auf 4, die die Winkel zwischen zwei parallelen Linien zeigt, die von einer Sekante geschnitten werden, bestimmen Sie den Wert aller Winkel im Bogenmaß, wobei Sie wissen, dass der Winkel A = π / 6 Bogenmaß ist.
Lösung
A und B sind zusätzliche Außenwinkel, also B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5 & pgr; / 6
Verweise
- Baldor, J. A. 1973. Flugzeug- und Raumgeometrie. Zentralamerikanisches Kultur.
- Mathematische Gesetze und Formeln. Winkelmesssysteme. Wiederhergestellt von: ingemecanica.com.
- Wentworth, G. Flugzeuggeometrie. Wiederhergestellt von: gutenberg.org.
- Wikipedia. Ergänzungswinkel. Wiederhergestellt von: es.wikipedia.com
- Wikipedia. Förderer. Wiederhergestellt von: es.wikipedia.com
- Zapata F. Goniómetro: Geschichte, Teile, Betrieb. Wiederhergestellt von: lifeder.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.