
Trachtenberg-Methode, woraus sie besteht, Beispiele
Das Trachtenberg-Methode ist ein System, mit dem arithmetische Operationen, hauptsächlich Multiplikationen, auf einfache und schnelle Weise ausgeführt werden können, sobald die Regeln bekannt und beherrscht sind.
Es wurde von dem in Russland geborenen Ingenieur Jakow Trachtenberg (1888-1953) als Gefangener der Nazis in einem Konzentrationslager entwickelt, um die geistige Gesundheit zu erhalten und gleichzeitig in Gefangenschaft zu bleiben..
Artikelverzeichnis
- 1 Woraus es besteht, Vor- und Nachteile
- 2 Beispiele
- 2.1 - Multiplizieren Sie eine Zahl mit 10 oder mit 11
- 2.2 - Multiplikation mit Zahlen von 12 bis 19
- 2.3 - Erweiterung der Multiplikationsregeln um 13,… bis 19
- 3 Regeln für Produkte nach 6, 7 und 5
- 3.1 - Multiplikation mit 6
- 3.2 - Multiplikation mit 7
- 3.3 - Multiplikation mit 5
- 4 Regeln für Produkte bis 9
- 5 Multiplikation mit 8, 4, 3 und 2
- 5.1 - Multiplikation mit 8
- 5.2 - Multiplikation mit 4
- 5.3 - Multiplikation mit 3
- 5.4 - Multiplikation mit 2
- 6 Mit zusammengesetzten Zahlen multiplizieren
- 6.1 Übung
- 7 Referenzen
Woraus es besteht, Vor- und Nachteile
Der Vorteil dieser Methode besteht darin, dass zur Durchführung der Multiplikation die Multiplikationstabellen zumindest teilweise nicht gespeichert werden müssen. Es reicht nur aus, zu wissen, wie man zählt und addiert sowie eine Ziffer durch zwei teilt.
Der Nachteil ist, dass es keine universelle Regel für das Multiplizieren mit einer beliebigen Zahl gibt, sondern dass die Regel je nach Multiplikator variiert. Die Muster sind jedoch nicht schwer zu merken und ermöglichen im Prinzip Operationen ohne die Hilfe von Papier und Bleistift..
In diesem Artikel konzentrieren wir uns auf die Regeln für eine schnelle Multiplikation.
Beispiele
Um die Methode anzuwenden, müssen die Regeln bekannt sein. Deshalb werden wir sie einzeln und anhand von Beispielen vorstellen:
- Multiplizieren Sie eine Zahl mit 10 oder mit 11
Regel für die Multiplikation mit 10
-Um eine beliebige Zahl mit 10 zu multiplizieren, fügen Sie einfach rechts eine Null hinzu. Zum Beispiel: 52 x 10 = 520.
Regeln für die Multiplikation mit 11
-Am Anfang und Ende der Abbildung wird eine Null hinzugefügt.
-Jede Ziffer wird mit dem Nachbarn rechts hinzugefügt und das Ergebnis unter der entsprechenden Ziffer der Originalfigur platziert.
-Wenn das Ergebnis neun überschreitet, wird die Einheit notiert und ein Punkt darauf platziert, um sich daran zu erinnern, dass wir eine Einheit haben, die in der Summe der nächsten Zahl mit ihrem Nachbarn auf der rechten Seite addiert wird.
Detailliertes Beispiel für die Multiplikation mit 11
Multiplizieren Sie 673179 mit 11
06731790 x 11 =
--
= 7404969
Die Schritte, die erforderlich sind, um zu diesem Ergebnis zu gelangen, sind wie folgt dargestellt:
-Die 1 der Einheit des Multiplikators (11) wurde mit der 9 des Multiplikators (0) multipliziert6731790) und 0 wurden hinzugefügt. Die Einheitsziffer des Ergebnisses wurde erhalten: 9.
-Dann multiplizieren wir 1 mit 7 und addieren neun zu 16 und wir tragen 1, wir setzen die zehnstellige Zahl: 6.
-Nach dem Multiplizieren von 1 mit 1 ergibt das Hinzufügen des Nachbarn auf der rechten Seite 7 plus 1, den er trug, das Ergebnis 9 für die hundert.
-Die nächste Zahl wird erhalten, indem 1 mit 3 plus dem Nachbarn 1 multipliziert wird 4 für die Tausenderstelle.
-Multiplizieren Sie 1 mit 7 und addieren Sie den Nachbarn 3, was zu 10 führt. Setzen Sie die Null (0) als zehntausendstellige Zahl und nimmt eine.
-Dann ergibt 1 mal 6 plus Nachbar 7 13 plus eine 1, die Ergebnisse 14 hatte, die 4 als hunderttausend Ziffer und nimmt 1.
-Schließlich wird 1 mit der zu Beginn hinzugefügten Null multipliziert, was Null plus den Nachbarn 6 plus Eins ergibt. Es stellt sich schließlich heraus 7 für die Ziffer, die den Millionen entspricht.
- Multiplikation mit Zahlen von 12 bis 19
So multiplizieren Sie eine beliebige Zahl mit 12:
-Am Anfang wird eine Null und am Ende der zu multiplizierenden Zahl eine weitere Null hinzugefügt.
-Jede Ziffer der zu multiplizierenden Zahl wird verdoppelt und mit dem Nachbarn rechts addiert.
-Wenn die Summe 10 überschreitet, wird eine Einheit zur nächsten Duplizierungsoperation hinzugefügt und mit dem Nachbarn summiert.
Beispiel für die Multiplikation mit 12
Multiplizieren Sie 63247 mit 12
0632470 x 12 =
-
758964
Die Details, um unter strikter Einhaltung der angegebenen Regeln zu diesem Ergebnis zu gelangen, sind in der folgenden Abbildung dargestellt:

- Erweiterung der Multiplikationsregeln um 13,… bis 19
Die Methode der Multiplikation mit 12 kann auf die Multiplikation mit 13, 14 bis 19 erweitert werden, indem einfach die Verdopplungsregel durch Verdreifachen für den Fall von dreizehn, Vervierfachen für den Fall von 14 usw. bis zum Erreichen von 19 geändert wird.
Regeln für Produkte von 6, 7 und 5
- Multiplikation mit 6
-Fügen Sie am Anfang und am Ende der Abbildung Nullen hinzu, um mit 6 zu multiplizieren.
-Fügen Sie jeder Ziffer rechts die Hälfte des Nachbarn hinzu, aber wenn die Ziffer ungerade ist, fügen Sie zusätzlich 5 hinzu.
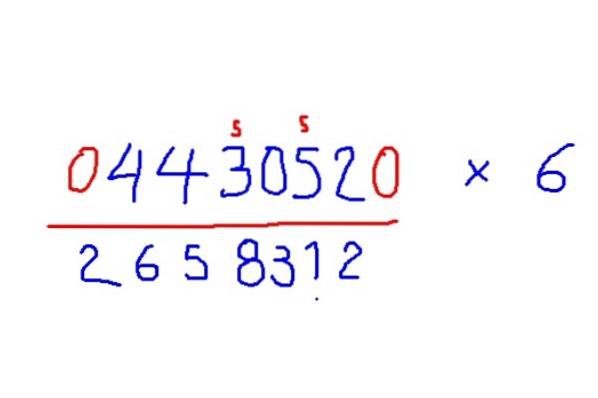
- Multiplikation mit 7
-Fügen Sie am Anfang und am Ende der zu multiplizierenden Zahl Nullen hinzu.
-Verdoppeln Sie jede Ziffer und addieren Sie die untere ganze Hälfte des Nachbarn. Wenn die Ziffer jedoch ungerade ist, addieren Sie zusätzlich 5.
Beispiel für die Multiplikation mit 7
-3412 mit 7 multiplizieren
-Das Ergebnis ist 23884. Um die Regeln anzuwenden, wird empfohlen, zuerst die ungeraden Ziffern zu erkennen und eine kleine 5 darüber zu platzieren, um daran zu denken, diese Zahl zum Ergebnis hinzuzufügen..
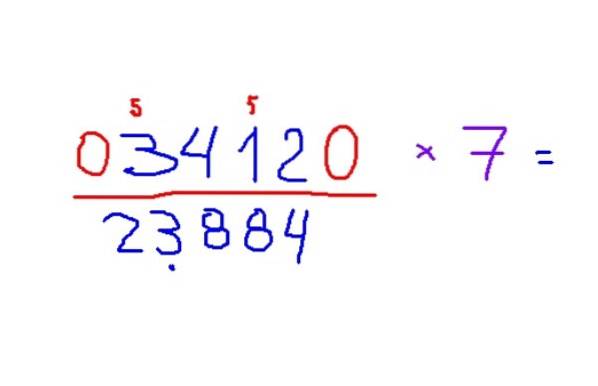
- Multiplikation mit 5
-Fügen Sie am Anfang und am Ende der zu multiplizierenden Zahl Nullen hinzu.
-Platzieren Sie unter jeder Ziffer die untere ganze Hälfte des Nachbarn rechts, aber wenn die Ziffer ungerade ist, addieren Sie zusätzlich 5.
Beispiel Multiplikation mit 5
Multiplizieren Sie 256413 mit 5
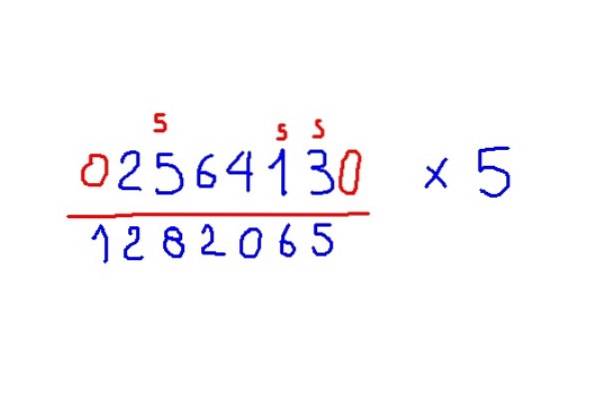
Regeln für Produkte bis 9
-Am Anfang wird eine Null hinzugefügt und am Ende der Figur eine weitere, die mit neun multipliziert wird.
-Die erste Ziffer rechts wird erhalten, indem die entsprechende Ziffer der zu multiplizierenden Zahl von 10 subtrahiert wird.
-Dann wird die nächste Ziffer von 9 abgezogen und der Nachbar addiert.
-Der vorherige Schritt wird wiederholt, bis wir die Null des Multiplikanden erreichen, wo wir 1 vom Nachbarn subtrahieren und das Ergebnis unter Null kopiert wird..
Beispiel für die Multiplikation mit 9
Multiplizieren Sie 8769 mit 9:
087690 x 9 =
--
78921
Operationen
10 - 9 = 1
(9-6) + 9 = 1zwei (das zwei und nimmt 1)
(9-7) + 1 + 6 =9
(9-8) +7 =8
(8-1) = 7
Multiplikation mit 8, 4, 3 und 2
-Fügen Sie am Anfang und am Ende der zu multiplizierenden Zahl Nullen hinzu.
-Für die erste Ziffer von rechts subtrahieren Sie von 10 und das Ergebnis wird verdoppelt.
-Wenn die folgenden Ziffern von 9 subtrahieren, wird das Ergebnis verdoppelt und der Nachbar hinzugefügt.
-Wenn Sie Null erreichen, subtrahieren Sie 2 vom Nachbarn auf der rechten Seite.
- Multiplikation mit 8
Beispiel für die Multiplikation mit 8
-789 mit 8 multiplizieren
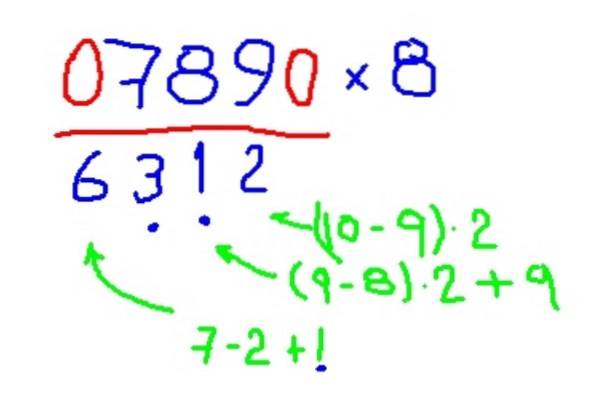
- Multiplikation mit 4
-Fügen Sie rechts und links vom Multiplikanden Nullen hinzu.
-Subtrahieren Sie die entsprechende Ziffer der Einheit von 10, indem Sie 5 addieren, wenn es sich um eine ungerade Ziffer handelt.
-Subtrahieren Sie jede Ziffer des Multiplikanden von 9 in der Form, indem Sie die Hälfte des Nachbarn rechts addieren, und wenn es sich um eine ungerade Ziffer handelt, addieren Sie zusätzlich 5.
-Wenn Sie die Null am Anfang des Multiplikanden erreichen, platzieren Sie die Hälfte des Nachbarn minus Eins.
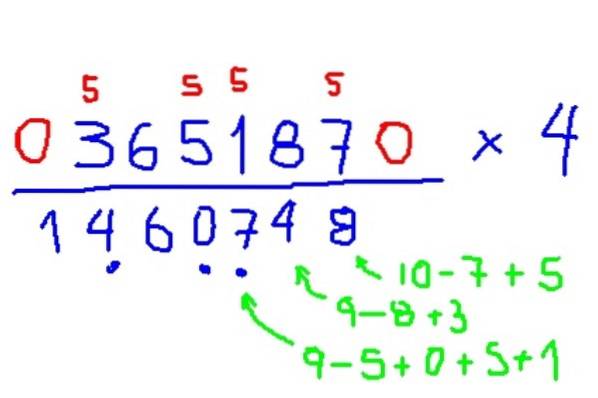
Beispiel für die Multiplikation mit 4
Multiplizieren Sie 365187 x 4
- Multiplikation mit 3
-Fügen Sie an jedem Ende des Multiplikanden Null hinzu.
-Subtrahieren Sie 10 minus der Einerstelle und addieren Sie 5, wenn es sich um eine ungerade Ziffer handelt.
-Subtrahieren Sie für die anderen Ziffern 9, verdoppeln Sie das Ergebnis, addieren Sie die Hälfte des Nachbarn und addieren Sie 5, wenn es ungerade ist..
-Wenn Sie die Null des Headers erreichen, platzieren Sie die untere ganzzahlige Hälfte des Nachbarn minus 2.
Beispiel für die Multiplikation mit 3
Multiplizieren Sie 2588 mit 3

- Multiplikation mit 2
-Fügen Sie an den Enden Nullen hinzu und verdoppeln Sie jede Ziffer, wenn sie 10 überschreitet, fügen Sie eine zur nächsten hinzu.
Beispiel Multiplikation mit 2
2374 mit 2 multiplizieren
023740 x 2
04748
Mit zusammengesetzten Zahlen multiplizieren
Es gelten die oben aufgeführten Regeln, aber die Ergebnisse werden links von der Anzahl der Stellen angezeigt, die Zehnern, Hunderten usw. entsprechen. Schauen wir uns das folgende Beispiel an:
Übung
Multiplizieren Sie 37654 mit 498
0376540 x 498
301232 Lineal für 8
338886 Regel für 9
150616 Lineal für 4
18751692 Endsumme
Verweise
- Cutler, Ann. 1960 Das Trachtenberg-Geschwindigkeitssystem der Grundmathematik. Doubleday & CO, NY.
- Dialnet. Schnelles grundlegendes mathematisches System. Wiederhergestellt von: dialnet.com
- Mathematische Ecke. Schnelle Multiplikation nach der Trachtenberg-Methode. Wiederhergestellt von: rinconmatematico.com
- Das Trachtenberg-Geschwindigkeitssystem der Grundmathematik. Wiederhergestellt von: trachtenbergspeedmath.com
- Wikipedia. Trachtenberg-Methode. Wiederhergestellt von: wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.