
Eigenschaften und Postulate des Dirac Jordan-Atommodells

Das Dirac-Jordan-Atommodell ist die relativistische Verallgemeinerung des Hamilton-Operators in der Gleichung, die die Quantenwellenfunktion des Elektrons beschreibt. Im Gegensatz zum Vorgängermodell, dem von Schrödinger, ist es nicht erforderlich, den Spin mittels des Pauli-Ausschlussprinzips aufzuerlegen, da er natürlich erscheint.
Darüber hinaus enthält das Dirac-Jordan-Modell relativistische Korrekturen, die Spin-Bahn-Wechselwirkung und den Darwin-Term, die für die Feinstruktur der elektronischen Ebenen des Atoms verantwortlich sind..

Ab 1928 wollten die Wissenschaftler Paul A. M. Dirac (1902-1984) und Pascual Jordan (1902-1980) die von Schrödinger entwickelte Quantenmechanik verallgemeinern und Einsteins Korrekturen der speziellen Relativitätstheorie einbeziehen.
Dirac geht von der Schrödinger-Gleichung aus, die aus einem Differentialoperator namens Hamilton besteht, der mit einer Funktion arbeitet, die als bekannt ist die Elektronenwellenfunktion. Schrödinger berücksichtigte jedoch nicht die relativistischen Effekte.
Die Lösungen der Wellenfunktion ermöglichen es uns, die Regionen zu berechnen, in denen sich das Elektron mit einer gewissen Wahrscheinlichkeit um den Kern befindet. Diese Regionen oder Zonen werden aufgerufen Orbitale und hängen von bestimmten diskreten Quantenzahlen ab, die die Energie und den Drehimpuls des Elektrons definieren.
Artikelverzeichnis
- 1 Postulate
- 1.1 Die vier Postulate von Dirac
- 2 Die Dirac-Gleichung
- 2.1 Das Dirac-Jordan-Atom
- 2.2 Relativistische Korrekturen des Energiespektrums
- 3 Artikel von Interesse
- 4 Referenzen
Postulate
In quantenmechanischen Theorien, ob relativistisch oder nicht, gibt es kein Konzept von Umlaufbahnen, da weder die Position noch die Geschwindigkeit des Elektrons gleichzeitig spezifiziert werden können. Darüber hinaus führt die Angabe einer der Variablen zu einer vollständigen Ungenauigkeit der anderen..
Der Hamilton-Operator ist seinerseits ein mathematischer Operator, der auf die Quantenwellenfunktion einwirkt und aus der Energie des Elektrons aufgebaut ist. Zum Beispiel hat ein freies Elektron eine Gesamtenergie E, die von seinem linearen Impuls abhängt p so:
E = (pzwei) / 2m
Um den Hamilton-Operator zu konstruieren, gehen wir von diesem Ausdruck aus und ersetzen ihn p vom Quantenoperator für Impuls:
p = -i ħ ∂ / ∂r
Es ist wichtig zu beachten, dass die Begriffe p Y. p sind unterschiedlich, da der erste der Impuls und der andere der Impuls ist Differentialoperator mit Schwung verbunden.
Zusätzlich ist i die imaginäre Einheit und ħ die Planck-Konstante geteilt durch 2π, auf diese Weise wird der Hamilton-Operator H des freien Elektrons erhalten:
H = (ħzwei/ 2m) ∂zwei / ∂rzwei
Um den Hamilton-Wert des Elektrons im Atom zu ermitteln, addieren Sie die Wechselwirkung des Elektrons mit dem Kern:
H = (ħ2 / 2m) ∂zwei / ∂rzwei - eΦ (r)
Im vorherigen Ausdruck ist -e die elektrische Ladung des Elektrons und Φ (r) das vom zentralen Kern erzeugte elektrostatische Potential.
Nun wirkt der Operator H auf die Wellenfunktion ψ gemäß der Schrödinger-Gleichung, die wie folgt geschrieben ist:
H ψ = (i ħ ∂ / ∂t) ψ
Diracs vier Postulate
Erstes Postulat: Die relativistische Wellengleichung hat die gleiche Struktur wie die Schrödinger-Wellengleichung. Was sich ändert, ist die H:
H ψ = (i ħ ∂ / ∂t) ψ
Zweites Postulat: Der Hamilton-Operator wird ausgehend von Einsteins Energie-Impuls-Beziehung konstruiert, die wie folgt geschrieben ist:
E = (mzwei c4 + pzwei czwei)1/2
In der vorherigen Beziehung haben wir die berühmte Gleichung E = mc, wenn das Teilchen einen Impuls p = 0 hatzwei Dies bezieht die Restenergie eines Teilchens der Masse m auf die Lichtgeschwindigkeit c.
Drittes Postulat: Um den Hamilton-Operator zu erhalten, wird dieselbe Quantisierungsregel verwendet, die in der Schrödinger-Gleichung verwendet wird:
p = -i ħ ∂ / ∂r
Am Anfang war nicht klar, wie man mit diesem Differentialoperator umgeht, der innerhalb einer Quadratwurzel wirkt, also machte sich Dirac daran, einen linearen Hamilton-Operator für den Impulsoperator zu erhalten, und daraus entstand sein viertes Postulat.
Viertes Postulat: Um die Quadratwurzel in der relativistischen Energieformel loszuwerden, schlug Dirac die folgende Struktur für E vorzwei::
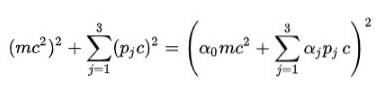
Natürlich ist es notwendig, die Alpha-Koeffizienten (α0, α1, α2, α3) zu bestimmen, damit dies wahr ist.
Diracs Gleichung
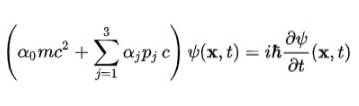
In ihrer kompakten Form gilt die Dirac-Gleichung als eine der schönsten mathematischen Gleichungen der Welt:
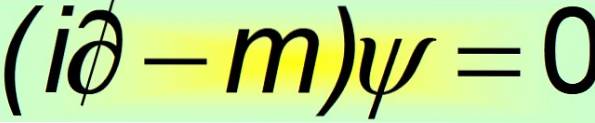
Und dann wird klar, dass die konstanten Alphas keine skalaren Größen sein können. Die einzige Möglichkeit, die Gleichheit des vierten Postulats zu erfüllen, besteht darin, dass es sich um 4 × 4 konstante Matrizen handelt, die als bekannt sind Dirac-Matrizen::
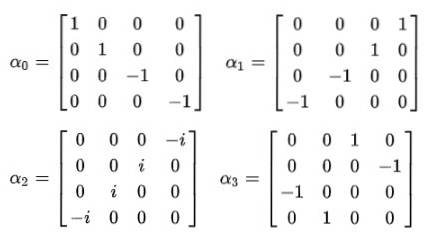
Es wird sofort beobachtet, dass die Wellenfunktion keine Skalarfunktion mehr ist und zu einem Vierkomponentenvektor namens wird Spinor::
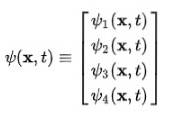
Das Dirac-Jordan-Atom
Um das Atommodell zu erhalten, ist es notwendig, von der Gleichung des freien Elektrons zu der des Elektrons in dem vom Atomkern erzeugten elektromagnetischen Feld überzugehen. Diese Wechselwirkung wird durch Einbeziehung des Skalarpotentials Φ und des Vektorpotentials berücksichtigt ZU im Hamiltonianer:
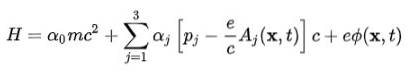
Die Wellenfunktion (Spinor), die sich aus der Einbeziehung dieses Hamilton-Operators ergibt, weist die folgenden Eigenschaften auf:
- Es erfüllt eine spezielle Relativitätstheorie, da es die intrinsische Energie des Elektrons berücksichtigt (erster Term des relativistischen Hamilton-Operators)
- Es hat vier Lösungen, die den vier Komponenten des Spinors entsprechen
- Die ersten beiden Lösungen entsprechen einer Spin + ½ und die andere Spin - ½
- Schließlich sagen die beiden anderen Lösungen die Existenz von Antimaterie voraus, da sie der von Positronen mit entgegengesetzten Spins entsprechen..
Der große Vorteil der Dirac-Gleichung besteht darin, dass die Korrekturen des grundlegenden Schrödinger-Hamilton-H (o) in mehrere Begriffe unterteilt werden können, die wir unten zeigen werden:
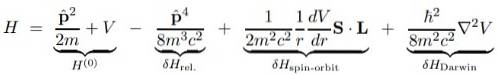
Im vorherigen Ausdruck ist V das Skalarpotential, da das Vektorpotential ZU ist null, wenn angenommen wird, dass das zentrale Proton stationär ist und daher nicht erscheint.
Der Grund, warum die Dirac-Korrekturen an den Schrödinger-Lösungen in der Wellenfunktion subtil sind. Sie ergeben sich aus der Tatsache, dass die letzten drei Terme des korrigierten Hamilton-Operators alle durch die Lichtgeschwindigkeit c des quadratischen Lichts geteilt werden, eine immense Zahl, die diese Terme numerisch klein macht.
Relativistische Korrekturen des Energiespektrums
Unter Verwendung der Dirac-Jordan-Gleichung finden wir Korrekturen am Energiespektrum des Elektrons im Wasserstoffatom. Korrekturen für Energie in Atomen mit mehr als einem Elektron in ungefährer Form werden auch durch eine Methodik gefunden, die als Störungstheorie bekannt ist..
In ähnlicher Weise ermöglicht das Dirac-Modell das Auffinden der Feinstrukturkorrektur in Wasserstoff-Energieniveaus..
Noch subtilere Korrekturen wie die Hyperfeinstruktur und die Lamb-Verschiebung werden jedoch von fortgeschritteneren Modellen wie z Quantenfeldtheorie, was genau durch die Beiträge des Dirac-Modells geboren wurde.
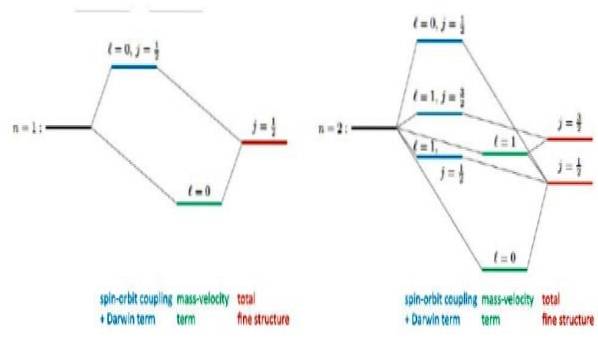
Die folgende Abbildung zeigt, wie Diracs relativistische Korrekturen der Energieniveaus aussehen:
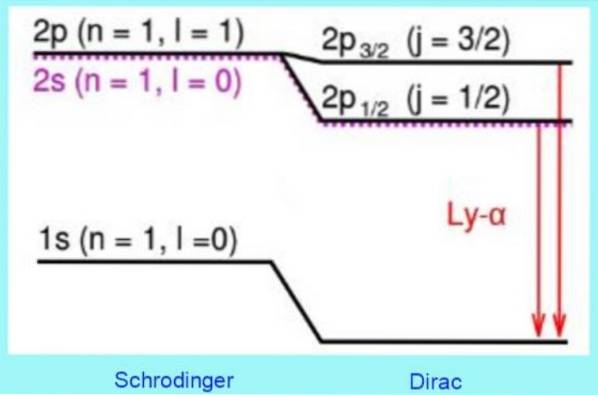
Beispielsweise sagen Lösungen der Dirac-Gleichung eine beobachtete Verschiebung auf Stufe 2s korrekt voraus. Dies ist die bekannte Feinstrukturkorrektur in der Lyman-Alpha-Linie des Wasserstoffspektrums (siehe Abbildung 3)..
Übrigens ist die Feinstruktur in der Atomphysik der Name für die Verdoppelung der Linien des Emissionsspektrums von Atomen, was eine direkte Folge des elektronischen Spins ist..
Artikel von Interesse
Atomic de Broglie Modell.
Chadwick-Atommodell.
Heisenberg-Atommodell.
Perrins Atommodell.
Thomsons Atommodell.
Dalton-Atommodell.
Schrödingers Atommodell.
Atommodell von Demokrit.
Atommodell von Leukipp.
Bohr-Atommodell.
Aktuelles Atommodell.
Verweise
- Atomtheorie. Von wikipedia.org wiederhergestellt.
- Elektronenmagnetisches Moment. Von wikipedia.org wiederhergestellt.
- Quanta: Ein Handbuch der Konzepte. (1974). Oxford University Press. Von Wikipedia.org wiederhergestellt.
- Dirac Jordan Atommodell. Von prezi.com wiederhergestellt.
- Das neue Quantenuniversum. Cambridge University Press. Von Wikipedia.org wiederhergestellt.

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.