
Bohr-Atommodellmerkmale, Postulate, Einschränkungen

Das Bohr-Atommodell ist die 1913 veröffentlichte Konzeption des dänischen Physikers Niels Bohr (1885-1962) über die Struktur des Atoms. Im Bohr-Atom besetzen die Elektronen um den Kern dank einer so genannten Einschränkung nur bestimmte zulässige Bahnen Quantisierung.
Für Bohr stimmte das Bild des Atoms als Miniatur-Sonnensystem mit Elektronen, die um den Kern kreisen, nicht ganz mit der Tatsache überein, dass elektrische Ladungen, wenn sie beschleunigt werden, Energie ausstrahlen..
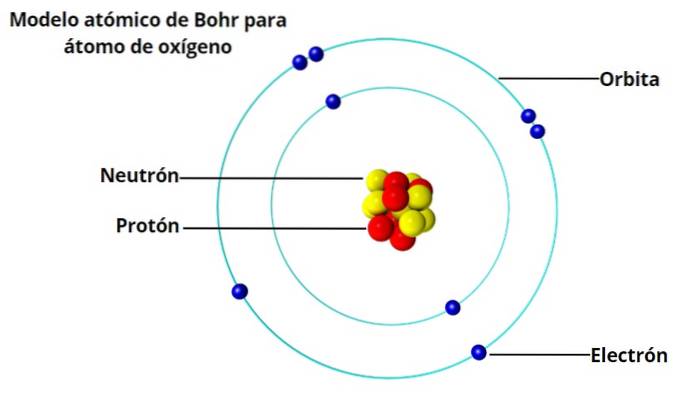
Ein solches Atom wäre nicht stabil, weil es früher oder später zusammenbrechen würde, weil die Elektronen sich in Richtung des Kerns drehen würden. Bis dahin waren die charakteristischen Lichtmuster, die Wasserstoff und andere Gase beim Erhitzen abgeben, seit 50 Jahren bekannt..
Das Muster oder Spektrum besteht aus einer Reihe heller Linien bestimmter sehr spezifischer Wellenlängen. Und das Wasserstoffatom kollabiert nicht, wenn es Licht emittiert.
Um zu erklären, warum das Atom trotz der Fähigkeit, elektromagnetische Energie abzustrahlen, stabil ist, schlug Bohr vor, dass der Drehimpuls nur bestimmte Werte und damit auch Energie annehmen könne. Dies ist mit Quantisierung gemeint.
Unter der Annahme, dass die Energie quantisiert wurde, hätte das Elektron die notwendige Stabilität, um nicht auf den Kern zuzustürmen, der das Atom zerstört..
Und das Atom strahlt nur dann Lichtenergie aus, wenn das Elektron von einer Umlaufbahn zur anderen übergeht, immer in diskreten Mengen. Auf diese Weise wird das Vorhandensein von Emissionsmustern in Wasserstoff erklärt..
Bohr komponierte so eine Vision des Atoms, indem er bekannte Konzepte aus der klassischen Mechanik mit neu entdeckten Konzepten wie der Planckschen Konstante, dem Photon, dem Elektron, dem Atomkern (Rutherford war Bohrs Mentor) und den oben genannten Fragenspektren integrierte.
Artikelverzeichnis
- 1 Hauptmerkmale des Bohr-Modells
- 1.1 Berechnung des Radius der Umlaufbahn des Elektrons
- 2 Postulate von Bohrs Atommodell
- 2.1 Elektronen beschreiben Kreisbahnen
- 2.2 Der Drehimpuls wird quantisiert
- 2.3 Elektronen emittieren oder absorbieren Photonen, wenn sie von einem Energiezustand in einen anderen übergehen
- 3 Einschränkungen
- 4 Artikel von Interesse
- 5 Referenzen
Hauptmerkmale des Bohr-Modells
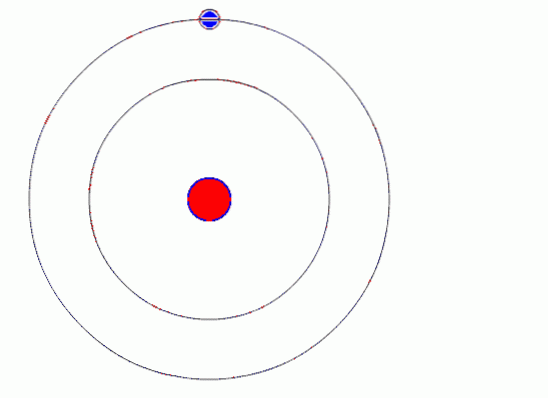
Bohrs Atommodell nimmt an, dass sich das Elektron durch die Wirkung der elektrostatischen Anziehungskraft von Coulomb in einer Kreisbahn um den Kern bewegt, und schlägt vor, dass der Drehimpuls des Elektrons quantisiert wird.
Mal sehen, wie man beide Konzepte in mathematischer Form integriert:
Sei L die Größe des Drehimpulses, m die Masse des Elektrons, v die Geschwindigkeit des Elektrons und r der Radius der Umlaufbahn. Um L zu berechnen, haben wir:
L = m⋅r⋅v
Bohr schlug vor, dass L gleich ganzzahligen Vielfachen der Konstanten h / 2π ist, wobei h die ist Plancksche Konstante, Dies wurde vor kurzem vom Physiker Max Planck (1858-1947) eingeführt, als er das Problem der von einem schwarzen Körper emittierten Energie löste, einem theoretischen Objekt, das das gesamte einfallende Licht absorbiert.
Sein Wert ist h = 6,626 × 10−34 J ・ s, während a h / 2π als bezeichnet wird ħ, was wird gelesen "H bar".
Daher bleibt der Drehimpuls L:
m⋅r⋅v = nħ, mit n = 1,2, 3 ...
Und aus dieser Bedingung werden die Radien der Bahnen abgeleitet, die für das Elektron zulässig sind, wie wir unten sehen werden.
Berechnung des Radius der Umlaufbahn des Elektrons
Im Folgenden nehmen wir das einfachste der Atome an: Wasserstoff, der aus einem einzelnen Proton und einem Elektron besteht, beide mit einer Ladung der Größe e.
Die Zentripetalkraft, die das Elektron in seiner Kreisbahn hält, wird durch elektrostatische Anziehung bereitgestellt, deren Größe F ist:
F = kezwei/ rzwei
Wobei k die elektrostatische Konstante des Coulombschen Gesetzes und r der Elektronen-Protonen-Abstand ist. Zu wissen, dass in einer Kreisbewegung die zentripetale Beschleunigung beic ist gegeben durch das Verhältnis zwischen dem Quadrat der Geschwindigkeit und dem Abstand r:
zuc = vzwei / r
Nach dem zweiten Newtonschen Gesetz ist die Nettokraft das Produkt aus der Masse m und der Beschleunigung:
mvzwei/ r = kezwei/ rzwei
Wenn wir den Radius r vereinfachen, erhalten wir:
m⋅vzweir = kezwei
Wenn wir diesen Ausdruck mit dem des Drehimpulses kombinieren, haben wir ein Gleichungssystem, gegeben durch:
1) mvzweir = kezwei
2) r = n ħ/ mv
Die Idee ist, das System zu lösen und r, den Radius der erlaubten Umlaufbahn, zu bestimmen. Eine kleine elementare Algebra führt zur Antwort:
r = (nħ)zwei / k⋅m⋅ezwei
Mit n = 1, 2, 3, 4, 5 ...
Für n = 1 haben wir den kleinsten der Radien, genannt Bohrradius zuoder mit einem Wert von 0,529 × 10−10 m. Die Radien der anderen Umlaufbahnen werden ausgedrückt als zuoder.
Auf diese Weise führt Bohr die Hauptquantenzahl ein n, unter Hinweis darauf, dass die zulässigen Radien eine Funktion der Planckschen Konstante, der elektrostatischen Konstante sowie der Masse und Ladung des Elektrons sind.
Bohrs Atommodell postuliert

Bohr kombiniert gekonnt die Newtonsche Mechanik mit neuen Entdeckungen, die in der zweiten Hälfte des neunzehnten und frühen zwanzigsten Jahrhunderts kontinuierlich gemacht wurden. Darunter das revolutionäre Konzept des "Quanten", von dem Planck selbst behauptete, nicht sehr überzeugt zu sein.
Durch seine Theorie konnte Bohr die Reihen im Wasserstoffspektrum zufriedenstellend erklären und Energieemissionen im ultravioletten und infraroten Bereich vorhersagen, die noch nicht beobachtet worden waren..
Wir können seine Postulate wie folgt zusammenfassen:
Elektronen beschreiben Kreisbahnen
Das Elektron dreht sich in einer stabilen Kreisbahn mit gleichmäßiger Kreisbewegung um den Kern. Die Bewegung ist auf die elektrostatische Anziehung zurückzuführen, die der Kern auf ihn ausübt.
Der Drehimpuls wird quantisiert
Der Drehimpuls des Elektrons wird gemäß dem Ausdruck quantisiert:
L = mvr = nħ
Wobei n eine ganze Zahl ist: n = 1, 2, 3, 4 ..., was dazu führt, dass sich das Elektron nur in bestimmten definierten Bahnen befinden kann, deren Radien sind:
r = (n ħ)zwei / k m ezwei
Elektronen emittieren oder absorbieren Photonen, wenn sie von einem Energiezustand in einen anderen übergehen
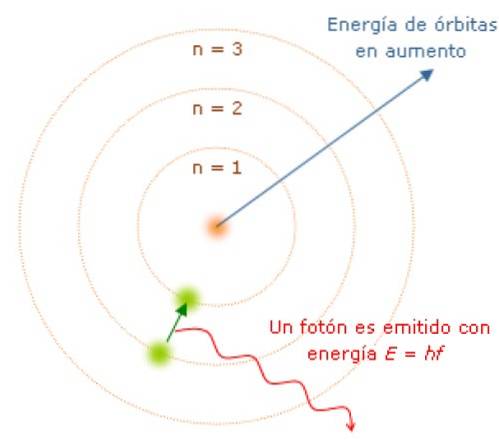
Da der Drehimpuls quantisiert wird, ist auch die Energie E quantisiert. Es kann gezeigt werden, dass E gegeben ist durch:


Das Elektronenvolt oder eV ist eine weitere Einheit für Energie, die in der Atomphysik weit verbreitet ist. Das negative Vorzeichen in der Energie stellt die Stabilität der Umlaufbahn sicher, was darauf hinweist, dass Arbeit geleistet werden müsste, um das Elektron von dieser Position zu trennen..
Während sich das Elektron in seiner Umlaufbahn befindet, absorbiert oder emittiert es kein Licht. Aber wenn es von einer Umlaufbahn mit höherer Energie zu einer niedrigeren springt, tut es das auch..
Die Frequenz f des emittierten Lichts hängt von der Differenz zwischen den Energieniveaus der Umlaufbahnen ab:
E = hf = E.Initiale - E.Finale
Einschränkungen
Das Bohr-Modell weist bestimmte Einschränkungen auf:
-Es wird nur erfolgreich auf das Wasserstoffatom angewendet. Versuche, es auf komplexere Atome anzuwenden, waren erfolglos.
-Es antwortet nicht, warum einige Umlaufbahnen stabil sind und andere nicht. Die Tatsache, dass die Energie im Atom quantisiert wurde, funktionierte sehr gut, aber das Modell lieferte keinen Grund, und das war etwas, das den Wissenschaftlern Unbehagen bereitete..
-Eine weitere wichtige Einschränkung besteht darin, dass die zusätzlichen Linien, die von Atomen in Gegenwart elektromagnetischer Felder emittiert werden (Zeeman-Effekt und Stark-Effekt), nicht erklärt wurden. Oder warum einige Linien des Spektrums intensiver waren als andere.
-Das Bohr-Modell berücksichtigt auch keine relativistischen Effekte, die berücksichtigt werden müssen, da experimentell festgestellt wurde, dass Elektronen Geschwindigkeiten erreichen können, die denen von Licht im Vakuum sehr nahe kommen..
-Es wird angenommen, dass es möglich ist, die Position und Geschwindigkeit des Elektrons genau zu kennen, aber was tatsächlich berechnet wird, ist die Wahrscheinlichkeit, dass das Elektron eine bestimmte Position einnimmt.
Trotz seiner Einschränkungen war das Modell zu dieser Zeit sehr erfolgreich, nicht nur um neue Entdeckungen in bereits bekannte Elemente zu integrieren, sondern auch, weil es neue Fragen aufwirft und deutlich macht, dass der Weg zu einer zufriedenstellenden Erklärung des Atoms in der Quantenmechanik liegt..
Artikel von Interesse
Schrödingers Atommodell.
Atomic de Broglie Modell.
Chadwick-Atommodell.
Heisenberg-Atommodell.
Perrins Atommodell.
Thomsons Atommodell.
Dalton-Atommodell.
Dirac Jordan Atommodell.
Atommodell von Demokrit.
Atommodell von Leukipp.
Sommerfeld-Atommodell.
Aktuelles Atommodell.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 2. Mc Graw Hill.
- Bohrs Atommodell. Wiederhergestellt von: sgpwe.izt.uam.mx.
- Serway, R. (2008). Physik für Wissenschaft und Technik. Band 2. 7 .. Ed. Lernen einbinden.
- Thomas Griffith, W. 2007. Konzeptphysik. Mcgraw Hügel.
- Tomé, C. Die Grenzen des Bohr-Modells. Notizbücher der wissenschaftlichen Kultur. Wiederhergestellt von: kulturacientifica.com.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.