
Grundlagen, Größen, Vektoren der Vektoralgebra
Das Vektoralgebra ist ein Zweig der Mathematik, der für die Untersuchung von Systemen linearer Gleichungen, Vektoren, Matrizen, Vektorräume und ihrer linearen Transformationen zuständig ist. Es bezieht sich unter anderem auf Bereiche wie Engineering, Auflösung von Differentialgleichungen, Funktionsanalyse, Operations Research, Computergrafik..
Ein weiterer Bereich, den die lineare Algebra übernommen hat, ist die Physik, da dadurch die Untersuchung physikalischer Phänomene entwickelt und mithilfe von Vektoren beschrieben werden konnte. Dies hat ein besseres Verständnis des Universums ermöglicht.

Artikelverzeichnis
- 1 Grundlagen
- 1.1 Geometrisch
- 1.2 Analytisch
- 1.3 Axiomatisch
- 2 Größen
- 2.1 Skalargröße
- 2.2 Vektorgröße
- 3 Was sind Vektoren??
- 3.1 Modul
- 3.2 Adresse
- 3.3 Sinn
- 4 Klassifikation von Vektoren
- 4.1 Fester Vektor
- 4.2 Freier Vektor
- 4.3 Gleitvektor
- 5 Eigenschaften von Vektoren
- 5.1 Teamlinsenvektoren
- 5.2 Äquivalente Vektoren
- 5.3 Gleichheit der Vektoren
- 5.4 Gegenüberliegende Vektoren
- 5.5 Einheitsvektor
- 5.6 Nullvektor
- 6 Komponenten eines Vektors
- 6.1 Beispiele
- 7 Operationen mit Vektoren
- 7.1 Addition und Subtraktion von Vektoren
- 7.2 Multiplikation von Vektoren
- 8 Referenzen
Grundlagen
Die Vektoralgebra entstand aus der Untersuchung der Quaternionen (Erweiterung reeller Zahlen) 1, i, j und k sowie aus der von Gibbs und Heaviside geförderten kartesischen Geometrie, die erkannte, dass Vektoren als Instrument zur Darstellung verschiedener physikalischer Phänomene dienen würden.
Die Vektoralgebra wird anhand von drei Grundlagen untersucht:
Geometrisch
Vektoren werden durch Linien dargestellt, die eine Ausrichtung haben, und Operationen wie Addition, Subtraktion und Multiplikation mit reellen Zahlen werden durch geometrische Methoden definiert..
Analytisch
Die Beschreibung von Vektoren und ihrer Operationen erfolgt mit Zahlen, die als Komponenten bezeichnet werden. Diese Art der Beschreibung ist das Ergebnis einer geometrischen Darstellung, da ein Koordinatensystem verwendet wird.
Axiomatisch
Eine Beschreibung der Vektoren erfolgt unabhängig vom Koordinatensystem oder einer beliebigen Art der geometrischen Darstellung.
Die Untersuchung von Figuren im Raum erfolgt durch ihre Darstellung in einem Bezugssystem, das in einer oder mehreren Dimensionen vorliegen kann. Zu den Hauptsystemen gehören:
- Eindimensionales System, dh eine Linie, bei der ein Punkt (O) den Ursprung darstellt und ein anderer Punkt (P) den Maßstab (die Länge) und seine Richtung bestimmt:
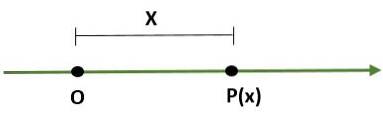
- Rechteckiges Koordinatensystem (zweidimensional), das aus zwei senkrechten Linien besteht, die als x-Achse und y-Achse bezeichnet werden und durch einen Punktursprung (O) verlaufen; Auf diese Weise wird die Ebene in vier Bereiche unterteilt, die als Quadranten bezeichnet werden. In diesem Fall ist ein Punkt (P) in der Ebene durch die Abstände gegeben, die zwischen den Achsen und P bestehen.
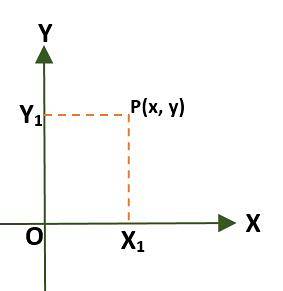
- Polarkoordinatensystem (zweidimensional). In diesem Fall besteht das System aus einem Punkt O (Ursprung), der als Pol bezeichnet wird, und einem Strahl mit Ursprung in O, der als Polarachse bezeichnet wird. In diesem Fall ist der Punkt P der Ebene in Bezug auf den Pol und die Polarachse durch den Winkel (Ɵ) gegeben, der durch den Abstand zwischen dem Ursprung und dem Punkt P gebildet wird.
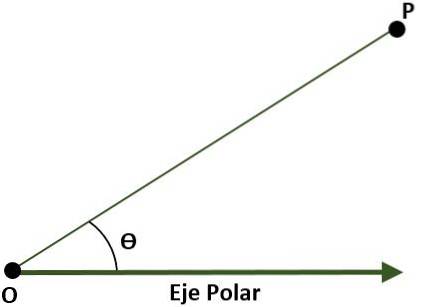
- Rechteckiges dreidimensionales System, gebildet aus drei senkrechten Linien (x, y, z), deren Ursprung ein Punkt O im Raum ist. Es werden drei Koordinatenebenen gebildet: xy, xz und yz; Der Raum wird in acht Regionen unterteilt, die als Oktanten bezeichnet werden. Die Referenz eines Punktes P im Raum ergibt sich aus den Abständen zwischen den Ebenen und P..
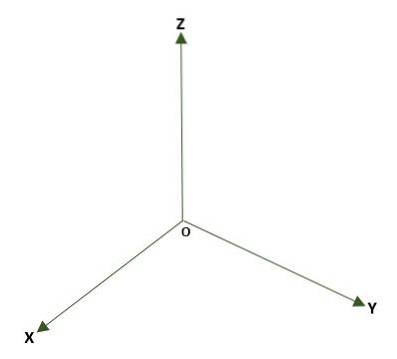
Größen
Eine Größe ist eine physikalische Größe, die wie bei einigen physikalischen Phänomenen durch einen numerischen Wert gezählt oder gemessen werden kann. Es ist jedoch oft notwendig, diese Phänomene mit anderen als numerischen Faktoren beschreiben zu können. Deshalb werden die Größen in zwei Typen eingeteilt:
Skalare Größe
Dies sind die Größen, die numerisch definiert und dargestellt werden. das heißt, durch ein Modul zusammen mit einer Maßeinheit. Beispielsweise:
a) Zeit: 5 Sekunden.
b) Masse: 10 kg.
c) Volumen: 40 ml.
d) Temperatur: 40 ºC.
Vektorgröße
Dies sind die Größen, die durch ein Modul zusammen mit einer Einheit sowie durch einen Sinn und eine Richtung definiert und dargestellt werden. Beispielsweise:
a) Geschwindigkeit: (5ȋ - 3ĵ) m / s.
b) Beschleunigung: 13 m / szwei;; S 45º E..
c) Kraft: 280 N, 120 °.
d) Gewicht: -40 ĵ kg-f.
Vektorgrößen werden grafisch durch Vektoren dargestellt.
Was sind Vektoren??
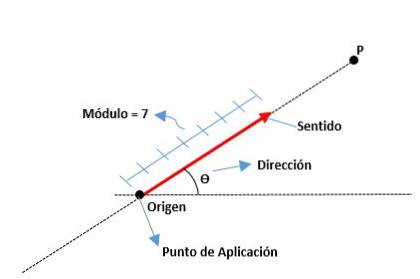
Vektoren sind grafische Darstellungen einer Vektorgröße; Das heißt, sie sind Liniensegmente, in denen ihr letztes Ende die Spitze eines Pfeils ist.
Diese werden durch die Modul- oder Segmentlänge, die Richtung, die durch die Pfeilspitze angezeigt wird, und die Richtung entsprechend der Linie bestimmt, zu der sie gehört. Der Ursprung eines Vektors wird auch als Anwendungspunkt bezeichnet.
Die Elemente eines Vektors sind wie folgt:
Modul
Dies ist der Abstand vom Ursprung bis zum Ende eines Vektors, dargestellt durch eine reelle Zahl zusammen mit einer Einheit. Beispielsweise:
| OM | = | A | = A = 6 cm
Richtung
Es ist das Maß für den Winkel, der zwischen der x-Achse (vom Positiv) und dem Vektor besteht, sowie die Kardinalpunkte (Nord, Süd, Ost und West) werden verwendet.
Sinn
Es wird durch die Pfeilspitze am Ende des Vektors angezeigt, die angibt, wohin es geht.
Klassifikation von Vektoren
Im Allgemeinen werden Vektoren wie folgt klassifiziert:
Fester Vektor
Es ist eines, dessen Anwendungspunkt (Ursprung) festgelegt ist; Das heißt, es bleibt mit einem Punkt im Raum verbunden, sodass es sich darin nicht bewegen kann.
Freier Vektor
Es kann sich frei im Raum bewegen, da sich sein Ursprung zu einem beliebigen Punkt bewegt, ohne sein Modul, seine Richtung oder Richtung zu ändern..
Schiebereglervektor
Es ist eines, das seinen Ursprung entlang seiner Wirkungslinie übertragen kann, ohne sein Modul, seine Richtung oder Richtung zu ändern..
Eigenschaften von Vektoren
Zu den Haupteigenschaften von Vektoren gehören:
Vektoren Teamlinsen
Sie sind jene freien Vektoren, die das gleiche Modul, die gleiche Richtung (oder sie sind parallel) und den gleichen Sinn wie ein Gleitvektor oder ein fester Vektor haben.
Äquivalente Vektoren
Es tritt auf, wenn zwei Vektoren dieselbe Richtung haben (oder parallel sind), denselben Sinn haben und trotz unterschiedlicher Module und Anwendungspunkte dieselben Effekte verursachen.
Vektorgleichheit
Diese haben das gleiche Modul, die gleiche Richtung und den gleichen Sinn, auch wenn ihre Startpunkte unterschiedlich sind, wodurch sich ein paralleler Vektor selbst verschieben kann, ohne ihn zu beeinflussen..
Gegenüberliegende Vektoren
Sie sind diejenigen, die das gleiche Modul und die gleiche Richtung haben, aber ihr Sinn ist entgegengesetzt.
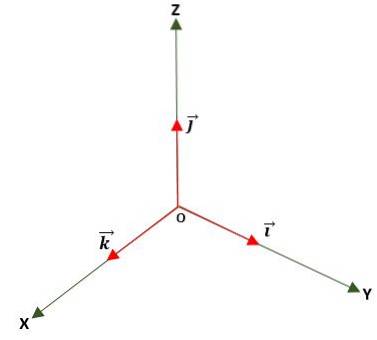
Einheitsvektor
Es ist eines, bei dem das Modul gleich der Einheit (1) ist. Dies wird durch Teilen des Vektors durch sein Modul erhalten und wird verwendet, um die Richtung und den Sinn eines Vektors entweder in der Ebene oder im Raum unter Verwendung der Basis- oder normalisierten Einheitsvektoren zu bestimmen, die sind:
Nullvektor
Es ist derjenige, dessen Modul gleich 0 ist; Das heißt, sein Ursprungs- und Endpunkt fallen am selben Punkt zusammen.
Komponenten eines Vektors
Die Komponenten eines Vektors sind die Werte der Projektionen des Vektors auf die Achsen des Referenzsystems; Abhängig von der Zerlegung des Vektors, die auf zwei oder dreidimensionalen Achsen liegen kann, werden zwei bzw. drei Komponenten erhalten..
Die Komponenten eines Vektors sind reelle Zahlen, die positiv, negativ oder sogar null (0) sein können..
Wenn wir also einen Vektor Ā mit Ursprung in einem rechteckigen Koordinatensystem in der xy-Ebene (zweidimensional) haben, ist die Projektion auf der x-Achse Āx und die Projektion auf der y-Achse ist Āy. Somit wird der Vektor als die Summe seiner Komponentenvektoren ausgedrückt.
Beispiele
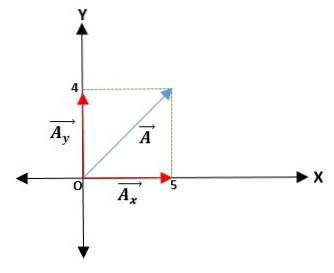
Erstes Beispiel
Wir haben einen Vektor Ā, der vom Ursprung ausgeht und dessen Koordinaten angegeben sind. Somit ist der Vektor Ā = (Āx;; ZUY.) = (4; 5) cm.
Wenn der Vektor Ā am Ursprung eines dreidimensionalen dreieckigen Koordinatensystems (im Raum) x, y, z zu einem anderen Punkt (P) wirkt, sind die Projektionen auf seinen Achsen Āx, Āy und Āz; Somit wird der Vektor als die Summe seiner drei Komponentenvektoren ausgedrückt.
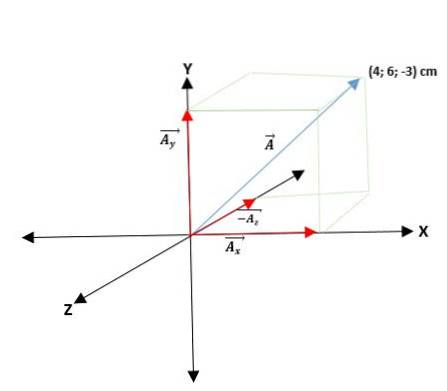
Zweites Beispiel
Wir haben einen Vektor Ā, der vom Ursprung ausgeht und dessen Koordinaten angegeben sind. Somit ist der Vektor Ā = (A.x;; ZUY; ZUz) = (4; 6; -3) cm.
Vektoren mit ihren rechteckigen Koordinaten können als Basisvektoren ausgedrückt werden. Dazu müssen Sie nur jede Koordinate mit ihrem jeweiligen Einheitsvektor so multiplizieren, dass sie für die Ebene und den Raum wie folgt lautet:
Für das Flugzeug gilt: Ā = A.xi + A.Y.j.
Für den Raum: Ā = A.xi + A.Y.j + A.zk.
Vektoroperationen
Es gibt viele Größen, die ein Modul, einen Sinn und eine Richtung haben, wie z. B. Beschleunigung, Geschwindigkeit, Verschiebung, Kraft..
Diese werden in verschiedenen Bereichen der Wissenschaft angewendet, und um sie anzuwenden, ist es in einigen Fällen erforderlich, Operationen wie Addition, Subtraktion, Multiplikation und Division von Vektoren und Skalaren durchzuführen..
Addition und Subtraktion von Vektoren
Das Addieren und Subtrahieren von Vektoren wird als einzelne algebraische Operation betrachtet, da die Subtraktion als Summe geschrieben werden kann; Zum Beispiel kann die Subtraktion der Vektoren Ā und Ē ausgedrückt werden als:
Ā - Ē = Ā + (-Ē)
Es gibt verschiedene Methoden, um die Addition und Subtraktion von Vektoren durchzuführen: Sie können grafisch oder analytisch sein.
Grafische Methoden
Wird verwendet, wenn ein Vektor ein Modul, einen Sinn und eine Richtung hat. Dazu werden Linien gezeichnet, die eine Figur bilden, die später zur Ermittlung des Ergebnisses beiträgt. Zu den bekanntesten gehören:
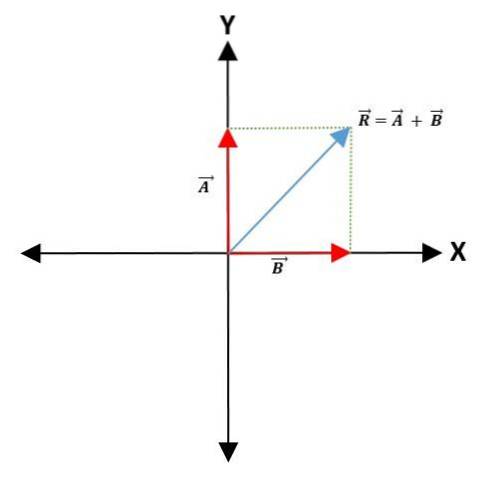
Parallelogrammmethode
Um zwei Vektoren zu addieren oder zu subtrahieren, wird auf der Koordinatenachse ein gemeinsamer Punkt ausgewählt, der den Ursprungspunkt der Vektoren darstellt, wobei Modul, Richtung und Richtung beibehalten werden..
Linien werden dann parallel zu den Vektoren gezeichnet, um ein Parallelogramm zu bilden. Der resultierende Vektor ist die Diagonale, die vom Ursprungspunkt beider Vektoren zum Scheitelpunkt des Parallelogramms führt:
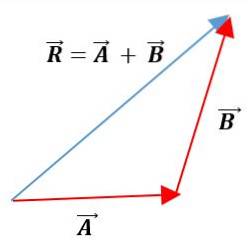
Dreiecksmethode
Bei dieser Methode werden die Vektoren nacheinander platziert, wobei ihre Module, Richtungen und Richtungen beibehalten werden. Der resultierende Vektor ist die Vereinigung des Ursprungs des ersten Vektors mit dem Ende des zweiten Vektors:
analytische Methoden
Zwei oder mehr Vektoren können durch eine geometrische oder Vektormethode addiert oder subtrahiert werden:
Geometrische Methode
Wenn zwei Vektoren ein Dreieck oder Parallelogramm bilden, können der Modul und die Richtung des resultierenden Vektors unter Verwendung der Gesetze von Sinus und Cosinus bestimmt werden. Somit ist das Modul des resultierenden Vektors unter Anwendung des Kosinusgesetzes und nach der Dreiecksmethode gegeben durch:
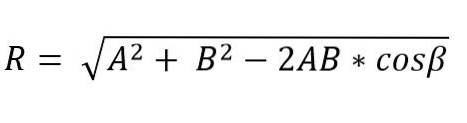
In dieser Formel ist β der Winkel gegenüber der Seite R, und dieser ist gleich 180º - Ɵ.
Stattdessen ist nach der Parallelogrammmethode der Modul des resultierenden Vektors:
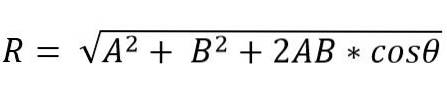
Die Richtung des resultierenden Vektors ist durch den Winkel (α) gegeben, der mit einem der Vektoren das Ergebnis bildet.
Nach dem Sinusgesetz kann die Addition oder Subtraktion von Vektoren auch nach der Dreieck- oder Parallelogrammmethode erfolgen, wobei zu wissen ist, dass in jedem Dreieck die Seiten proportional zu den Sinuskurven der Winkel sind:
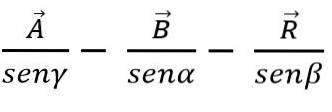
Vektormethode
Dies kann auf zwei Arten erfolgen: abhängig von seinen rechteckigen Koordinaten oder seinen Basisvektoren.
Dies kann durch Verschieben der zu addierenden oder zu subtrahierenden Vektoren in Richtung des Koordinatenursprungs und dann aller Projektionen auf jeder der Achsen für die Ebene (x, y) oder den Raum (x und Z) erfolgen. Schließlich werden seine Komponenten algebraisch hinzugefügt. Für das Flugzeug ist es also:
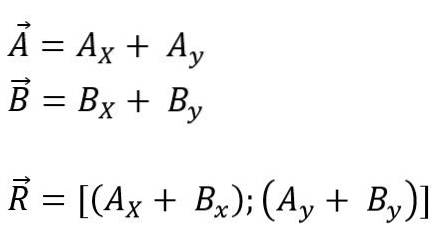
Der Modul des resultierenden Vektors ist:
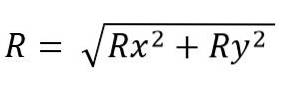
Während für den Raum ist es:
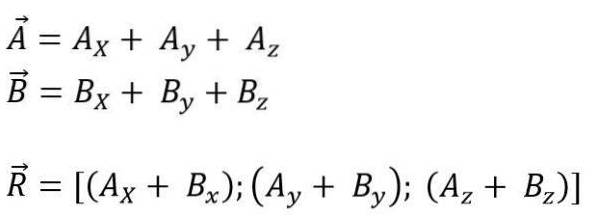
Der Modul des resultierenden Vektors ist:
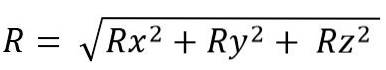
Wenn Vektorsummen ausgeführt werden, werden verschiedene Eigenschaften angewendet:
- Assoziative Eigenschaft: Das Ergebnis ändert sich nicht, wenn zuerst zwei Vektoren und dann ein dritter Vektor hinzugefügt werden.
- Kommutative Eigenschaft: Die Reihenfolge der Vektoren ändert das Ergebnis nicht.
- Vektorverteilungseigenschaft: Wenn ein Skalar mit der Summe zweier Vektoren multipliziert wird, entspricht dies der Multiplikation des Skalars mit jedem Vektor.
- Skalare Verteilungseigenschaft: Wenn ein Vektor mit der Summe zweier Skalare multipliziert wird, entspricht dies der Multiplikation des Vektors für jeden Skalar.
Multiplikation von Vektoren
Die Multiplikation oder das Produkt von Vektoren könnte als Addition oder Subtraktion erfolgen, aber auf diese Weise verliert die physikalische Bedeutung und wird in Anwendungen fast nie gefunden. Daher sind im Allgemeinen die am häufigsten verwendeten Produkttypen das Skalar- und das Vektorprodukt.
Skalarprodukt
Es ist auch als Punktprodukt zweier Vektoren bekannt. Wenn die Module zweier Vektoren mit dem Kosinus des kleinsten zwischen ihnen gebildeten Winkels multipliziert werden, wird ein Skalar erhalten. Um ein Skalarprodukt zwischen zwei Vektoren auszudrücken, wird ein Punkt zwischen ihnen platziert. Dies kann wie folgt definiert werden:
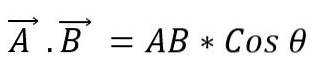
Der Wert des Winkels, der zwischen den beiden Vektoren besteht, hängt davon ab, ob sie parallel oder senkrecht sind. Sie müssen also:
- Wenn die Vektoren parallel sind und den gleichen Sinn haben, ist Cosinus 0º = 1.
- Wenn die Vektoren parallel sind und entgegengesetzte Richtungen haben, ist der Kosinus 180º = -1.
- Wenn die Vektoren senkrecht sind, ist Cosinus 90º = 0.
Dieser Winkel kann auch berechnet werden, wenn man weiß:

Das Punktprodukt hat folgende Eigenschaften:
- Kommutative Eigenschaft: Die Reihenfolge der Vektoren ändert den Skalar nicht.
-Verteilungseigenschaft: Wenn ein Skalar mit der Summe zweier Vektoren multipliziert wird, entspricht dies der Multiplikation des Skalars mit jedem Vektor.
Vektorprodukt
Die Vektormultiplikation oder das Kreuzprodukt zweier Vektoren A und B führt zu einem neuen Vektor C und wird unter Verwendung einer Kreuzung zwischen den Vektoren ausgedrückt:
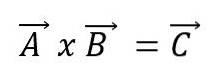
Der neue Vektor hat seine eigenen Eigenschaften. Dieser Weg:
- Die Richtung: Dieser neue Vektor verläuft senkrecht zur Ebene, die durch die ursprünglichen Vektoren bestimmt wird.
- Die Richtung: Dies wird mit der Rechtsregel bestimmt, bei der der Vektor A in Richtung B gedreht wird, wobei die Drehrichtung mit den Fingern angegeben wird, und die Richtung des Vektors mit dem Daumen markiert wird.
- Das Modul: wird durch die Multiplikation der Module der Vektoren AxB mit dem Sinus des kleinsten Winkels bestimmt, der zwischen diesen Vektoren besteht. Es wird ausgedrückt:
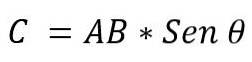
Der Wert des Winkels, der zwischen den beiden Vektoren besteht, hängt davon ab, ob sie parallel oder senkrecht sind. Es ist also möglich, Folgendes anzugeben:
- Wenn die Vektoren parallel sind und den gleichen Sinn haben, ist Sinus 0º = 0.
- Wenn die Vektoren parallel sind und entgegengesetzte Richtungen haben, ist Sinus 180º = 0.
- Wenn die Vektoren senkrecht sind, ist Sinus 90º = 1.
Wenn ein Vektorprodukt als Funktion seiner Basisvektoren ausgedrückt wird, haben wir:
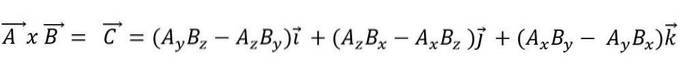
Das Punktprodukt hat folgende Eigenschaften:
- Es ist nicht kommutativ: Die Reihenfolge der Vektoren verändert den Skalar.
- Verteilungseigenschaft: Wenn ein Skalar mit der Summe zweier Vektoren multipliziert wird, entspricht dies der Multiplikation des Skalars mit jedem Vektor.
Verweise
- Altman Naomi, M. K. (2015). "Einfache lineare Regression." Naturmethoden .
- Angel, A. R. (2007). Elementare Algebra. Pearson Ausbildung,.
- Arthur Goodman, L. H. (1996). Algebra und Trigonometrie mit analytischer Geometrie. Pearson Ausbildung.
- Gusiatnikov, P. & Reznichenko, S. (s.f.). Vektoralgebra in Beispielen. Moskau: Mir.
- Lay, D. C. (2007). Lineare Algebra und ihre Anwendungen. Pearson Ausbildung.
- Llinares, J. F. (2009). Lineare Algebra: Vektorraum. Euklidischer Vektorraum. Universität von Alicante.
- Mora, J. F. (2014). Lineare Algebra. Heimat.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.