Das Beer-Lambert-Gesetz (Beer-Bouguer) bezieht sich auf die Absorption elektromagnetischer Strahlung einer oder mehrerer chemischer Spezies mit ihrer Konzentration und der Entfernung, die Licht bei Teilchen-Photonen-Wechselwirkungen zurücklegt. Dieses Gesetz vereint zwei Gesetze in einem.
Das Bouguer-Gesetz (obwohl die Anerkennung mehr auf Heinrich Lambert gefallen ist) legt fest, dass eine Probe mehr Strahlung absorbiert, wenn die Abmessungen des absorbierenden Mediums oder Materials größer sind; speziell seine Dicke, die der Abstand ist l dass sich das Licht beim Betreten und Verlassen bewegt.
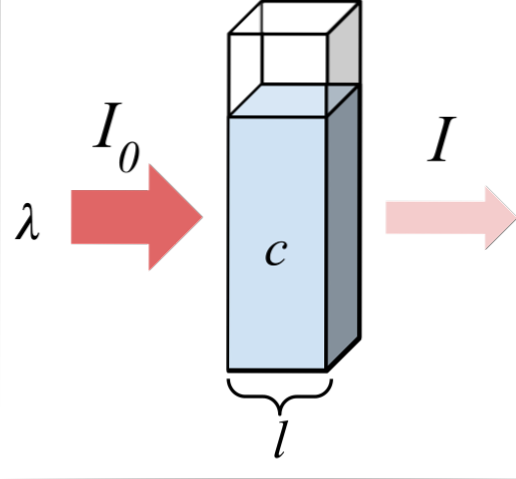
Das obere Bild zeigt die Absorption von monochromatischer Strahlung; das heißt, bestehend aus einer einzelnen Wellenlänge, λ. Das absorbierende Medium befindet sich in einer optischen Zelle, deren Dicke beträgt l, und enthält chemische Spezies mit einer Konzentration c.
Der Lichtstrahl hat eine Anfangs- und Endintensität, die durch die Symbole I gekennzeichnet ist0 bzw. ich. Beachten Sie, dass ich nach der Wechselwirkung mit dem absorbierenden Medium kleiner als ich bin0, was zeigt, dass es eine Absorption von Strahlung gab. Je älter sie sind c Y. l, kleiner werde ich in bezug auf mich sein0;; Das heißt, es wird mehr Absorption und weniger geben Durchlässigkeit.
Artikelverzeichnis
Das obige Bild umfasst dieses Gesetz perfekt. Die Absorption von Strahlung in einer Probe nimmt in Abhängigkeit von exponentiell zu oder ab c oder l. Um das Gesetz vollständig und leicht zu verstehen, ist es notwendig, seine mathematischen Aspekte zu umgehen.
Wie gerade erwähnt, ich0 und I sind die Intensitäten des monochromatischen Lichtstrahls vor bzw. nach dem Licht. Einige Texte bevorzugen die Verwendung der Symbole P.0 und P, die sich auf die Energie der Strahlung und nicht auf ihre Intensität beziehen. Hier wird die Erklärung anhand der Intensitäten fortgesetzt.
Um die Gleichung dieses Gesetzes zu linearisieren, muss der Logarithmus angewendet werden, im Allgemeinen die Basis 10:
Log (I.0/ I) = εlc
Der Begriff (I.0/ I) gibt an, um wie viel die Intensität des Strahlungsprodukts der Absorption abnimmt. Lamberts Gesetz berücksichtigt nur l (εl), während Biers Gesetz l ignoriert, aber Orte c stattdessen (εc). Die obere Gleichung ist die Vereinigung beider Gesetze und daher der allgemeine mathematische Ausdruck für das Beer-Lambert-Gesetz.
Die Extinktion wird durch den Begriff Log (I) definiert0/ ICH). Somit wird die Gleichung wie folgt ausgedrückt:
A = εlc
Wobei ε der Extinktionskoeffizient oder das molare Absorptionsvermögen ist, das bei einer gegebenen Wellenlänge eine Konstante ist.
Es ist zu beachten, dass, wenn die Dicke des absorbierenden Mediums wie & egr; konstant gehalten wird, die Absorption A nur von der Konzentration abhängt c, von absorbierenden Arten. Es ist auch eine lineare Gleichung, y = mx, wobei Y. ist A und x es ist c.
Mit zunehmender Absorption nimmt die Durchlässigkeit ab; das heißt, wie viel Strahlung nach Absorption übertragen werden kann. Sie sind daher invers. Ja ich0/ I gibt den Absorptionsgrad I / I an0 gleich Durchlässigkeit. Das wissen:
Ich / ich0 = T.
(ICH0/ I) = 1 / T.
Log (I.0/ I) = Log (1 / T)
Aber Log (ich0/ I) ist auch gleich Absorption. Die Beziehung zwischen A und T ist also:
A = Log (1 / T)
Und die Eigenschaften von Logarithmen anwenden und wissen, dass Log1 gleich 0 ist:
A = -LogT
Die Durchlässigkeiten werden normalerweise in Prozent ausgedrückt:
% T = I / I.0∙ 100
Wie zuvor angegeben, entsprechen die Gleichungen einer linearen Funktion; Daher wird erwartet, dass sie bei der grafischen Darstellung eine Linie ergeben.
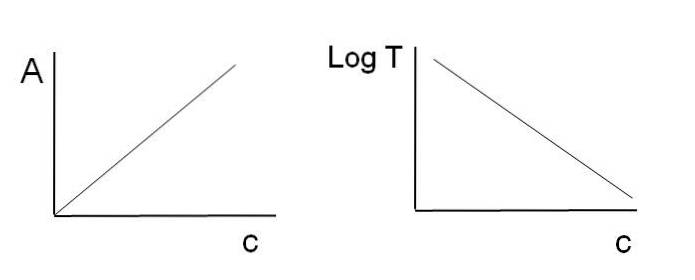
Beachten Sie, dass sich links neben dem Bild oben die Linie befindet, die durch grafische Darstellung von A erhalten wird c, und rechts die Linie, die dem Diagramm von LogT entspricht c. Einer hat eine positive Steigung und der andere eine negative; Je höher die Extinktion, desto geringer die Durchlässigkeit.
Dank dieser Linearität kann die Konzentration der absorbierenden chemischen Spezies (Chromophore) bestimmt werden, wenn bekannt ist, wie viel Strahlung sie absorbieren (A) oder wie viel Strahlung übertragen wird (LogT). Wenn diese Linearität nicht beobachtet wird, wird gesagt, dass sie einer positiven oder negativen Abweichung des Beer-Lambert-Gesetzes gegenübersteht.
Im Allgemeinen werden einige der wichtigsten Anwendungen dieses Gesetzes nachstehend aufgeführt:
-Wenn eine chemische Spezies Farbe zeigt, ist dies ein beispielhafter Kandidat, der durch kolorimetrische Techniken analysiert werden kann. Diese basieren auf dem Beer-Lambert-Gesetz und ermöglichen die Bestimmung der Konzentration der Analyten als Funktion der mit einem Spektrophotometer erhaltenen Extinktionen..
-Es ermöglicht die Erstellung von Kalibrierkurven, mit denen unter Berücksichtigung des Matrixeffekts der Probe die Konzentration der interessierenden Spezies bestimmt wird.
-Es wird häufig zur Analyse von Proteinen verwendet, da mehrere Aminosäuren im ultravioletten Bereich des elektromagnetischen Spektrums signifikante Absorptionen aufweisen..
-Chemische Reaktionen oder molekulare Phänomene, die eine Farbänderung beinhalten, können unter Verwendung von Absorptionswerten bei einer oder mehreren Wellenlängen analysiert werden..
-Mit Hilfe der multivariaten Analyse können komplexe Chromophormischungen analysiert werden. Auf diese Weise kann die Konzentration aller Analyten bestimmt werden, und auch die Gemische können klassifiziert und voneinander unterschieden werden; Schließen Sie beispielsweise aus, ob zwei identische Mineralien aus demselben Kontinent oder einem bestimmten Land stammen.
Was ist die Absorption einer Lösung mit einer Durchlässigkeit von 30% bei einer Wellenlänge von 640 nm??
Um es zu lösen, gehen Sie einfach zu den Definitionen von Absorption und Transmission.
% T = 30
T = (30/100) = 0,3
Und da A = -LogT ist, ist die Berechnung einfach:
A = -Log 0,3 = 0,5228
Beachten Sie, dass es keine Einheiten gibt.
Wenn die Lösung aus der vorherigen Übung aus einer Spezies W besteht, deren Konzentration 2,30 ∙ 10 beträgt-4 M und unter der Annahme, dass die Zelle 2 cm dick ist: Wie hoch sollte ihre Konzentration sein, um eine Durchlässigkeit von 8% zu erhalten??
Es könnte direkt mit dieser Gleichung gelöst werden:
-LogT = εlc
Der Wert von & epsi; ist jedoch unbekannt. Daher muss es mit den vorherigen Daten berechnet werden, und es wird angenommen, dass es über einen weiten Konzentrationsbereich konstant bleibt:
ε = -LogT / lc
= (-Log 0,3) / (2 cm × 2,3 × 10-4 M)
= 1136,52 M.-1∙ cm-1
Und jetzt können Sie mit% T = 8 mit der Berechnung fortfahren:
c = -LogT / εl
= (-Log 0,08) / (1136,52 M.-1∙ cm-1 x 2 cm)
= 4,82 ≤ 10-4 M.
Dann reicht es aus, wenn die W-Spezies ihre Konzentration verdoppelt (4,82 / 2,3), um ihren Durchlässigkeitsprozentsatz von 30% auf 8% zu verringern..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.