
Trigonometrische Identitäten (Beispiele und Übungen)
Das trigonometrische Identitäten sind Beziehungen zwischen trigonometrischen Verhältnissen, die für jeden Wert der Variablen gelten. Beispielsweise:
tan & thgr; = sin & thgr; / cos & thgr;
Es ist eine trigonometrische Identität, die drei Verhältnisse des Winkels & thgr;, der Tangente, des Sinus und des Cosinus des Winkels in Beziehung setzt.

Diese Identität gilt für alle Werte mit Ausnahme derjenigen, die 0 zum Nenner machen. Der cos θ ist 0 für θ = ± π / 2, ± 3π / 2, ± 5π / 2… Ein weiteres Beispiel für eine trigonometrische Identität ist:
sin x. sek x. ctg x = 1
Artikelverzeichnis
- 1 Demo
- 2 Arten trigonometrischer Identitäten
- 2.1 - Grundlegende trigonometrische Identitäten
- 2.2 - Pythagoreische Identitäten
- 2.3 - Formeln für den Kosinus und den Sinus der Addition / Subtraktion von Winkeln
- 2.4 - Formeln für den Doppelwinkel
- 2.5 - Formeln für den halben Winkel
- 3 Gelöste Übungen
- 3.1 - Übung 1
- 3.2 - Übung 2
- 4 Referenzen
Demonstration
Es gibt zwei grundlegende Möglichkeiten, um zu zeigen, dass eine trigonometrische Identität wahr ist:
1- Durch bequeme algebraische Manipulationen eines der Mitglieder der Gleichheit in das andere verwandeln.
2- Entwickeln Sie beide Mitglieder der Gleichheit getrennt, bis die jeweiligen endgültigen Ausdrücke von jedem genau gleich sind.
In der vorgeschlagenen Identität werden wir die linke Seite der Gleichheit transformieren, für die wir ctg x und sec x in Form von Sinus und Cosinus wie folgt ausdrücken:
ctg x = cos x / sin x
sec x = 1 / cos x
Wir ersetzen diesen Ausdruck auf der linken Seite der Identität und vereinfachen:
sin x. (1 / cos x). (cos x / sin x) = (sin x. cos x / cos x. sin x) = 1
Und die Richtigkeit der Identität ist bereits überprüft.
Arten von trigonometrischen Identitäten
Es gibt verschiedene Klassen trigonometrischer Identitäten. Wir werden die wichtigsten im Folgenden kurz beschreiben:
- Grundlegende trigonometrische Identitäten
Wir unterscheiden zwei Arten grundlegender Identitäten:
I) Diejenigen, die durch die Grundverhältnisse Sinus, Cosinus und Tangens ausgedrückt werden:
- sec x = 1 / cos x
- cosec x / 1 / sin x
- ctg x = 1 / tg x
- tg x = sin x / cos x
- ctg x = cos x / sin x
II) Die aus der Parität abgeleiteten. Wir wissen aus seinem Diagramm, dass sin x eine ungerade Funktion ist, was bedeutet, dass:
sin (-x) = - sin x
Cos x ist seinerseits eine gerade Funktion, daher:
cos (-x) = cos x
Dann:
tg (-x) = sin (-x) / cos (-x) = -sen x / cos x
Ähnlich:
- cotg (-x) = -ctg x
- sec (-x) = sec x
- cosec (-x) = - cosec x
- Pythagoreische Identitäten
Sie ergeben sich aus der Anwendung des Satzes von Pythagoras auf das rechtwinklige Dreieck der Beine a und b und der Hypotenuse c. Wir werden sehen:
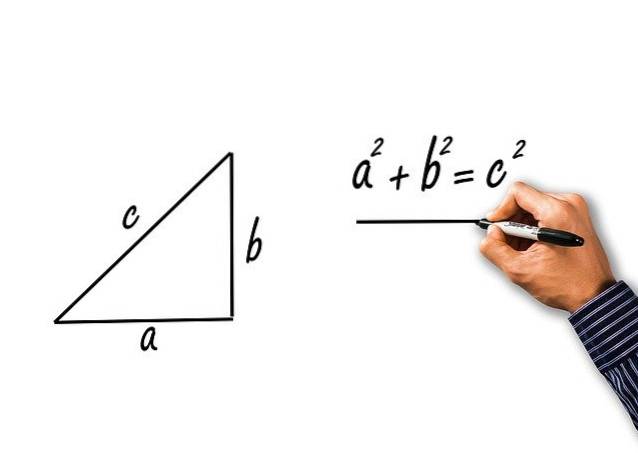
Der Satz von Pythagoras besagt:
czwei = azwei + bzwei
Alles teilen durch czwei::
czwei / czwei = (azwei / czwei) + (B.zwei / czwei)
Der Ausdruck auf der linken Seite ist 1 und erinnert daran, dass Sinus und Cosinus des spitzen Winkels α definiert sind als:
sin α = a / c
cos α = b / c
Ergebnis:
1 = (sin α)zwei + (cos α)zwei
Diese Identität ist bekannt als grundlegende Identität.
Das Verfahren kann durch Teilen durch a durchgeführt werdenzwei und Bzwei, was zu zwei weiteren Identitäten führt:
sekzwei α = 1 + tgzwei α
Erntezwei α = 1 + ctgzwei α
- Formeln für den Kosinus und den Sinus der Addition / Subtraktion von Winkeln
Die wichtigsten trigonometrischen Identitäten für Cosinus, Sinus und Tangens von Addition und Subtraktion sind wie folgt:


Beweis von sin (α + β) und cos (α + β)
Diese Identitäten können geometrisch oder auch durch Eulers Formel bewiesen werden:
undiα = cos α + i sin α
Mal sehen, was mit der Formel passiert, wenn die Summe zweier Winkel α und β eingesetzt wird:
undi (α +β) = cos (α + β) + i sin (α + β)
Dieser Ausdruck ist komplex, sein Realteil ist cos (α + β) und sein Imaginärteil ist i sin (α + β). Wir speichern dieses Ergebnis für die spätere Verwendung und konzentrieren uns auf die Entwicklung des Exponentialteils:
undi (α +β) = eiα ⋅ eiβ = (cos α + i sin α). (cos β + i sin β) =
= cos α⋅cos β + cos α⋅i sin β + i⋅sen α cos β - sin α⋅sen β
Der Realteil dieses Ausdrucks ist derjenige, der nicht mit der imaginären Einheit "i" multipliziert wird:
cos α⋅cos β - sin α. sin β
Der Imaginärteil ist daher:
i (cos α⋅sen β + sin α⋅cos β)
Damit zwei komplexe Ausdrücke gleich sind, muss der Realteil des einen dem Realteil des anderen entsprechen. Das gleiche passiert mit Imaginärteilen.
Wir nehmen das gespeicherte Ergebnis und vergleichen es damit:
cos α. cos β - sin α. sin β = cos (α + β)
i (cos α⋅sen β + sin α⋅cos β) = i sin (α + β)
sin (α + β) = (cos α. sin β + sin α⋅cos β)
- Formeln für den Doppelwinkel
In den vorhergehenden Formeln nehmen wir β = α und entwickeln:
sin (α + α) = sin 2 α = sin α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α
cos (α + α) = cos 2 α = cos α⋅cos α - sin α⋅sen α = coszwei α - Sünde zwei α
tg (α + α) = tg 2 α = [tg α + tg α] / [1 - tg α · tg α] = 2 tg α / 1 - tgzwei α
Wenn wir im zweiten Ausdruck cos ersetzenzwei α = 1 - sinzwei α wird erhalten:
cos 2 α = coszwei α - (1-coszwei α) = 2 coszwei α -1
- Formeln für den halben Winkel
In diesem letzten Ausdruck ersetzen wir α / 2 durch α, das Folgende bleibt:
cos α = 2 cos zwei(α / 2) -1
Lösen nach:


Gelöste Übungen
- Übung 1
Zeige, dass:

Wir werden den linken Begriff algebraisch so bearbeiten, dass er wie der richtige aussieht. Da sin x im richtigen Term erscheint, besteht der erste Schritt darin, cos auszudrückenzweix in Bezug auf sin x, so dass alles in Bezug auf das gleiche trigonometrische Verhältnis ist:
Dann wird 1 - Sünde berücksichtigtzwei x weil es ein Unterschied von perfekten Quadraten ist. Dazu wird die grundlegende Identität gelöscht:
coszweix = 1 - sinzwei x
1 - senzwei x = (1 - sin x) (1 + sinx)
Und die Faktorisierung wird im ursprünglichen Ausdruck ersetzt:

Der Begriff (1-sinx) wird vereinfacht und es bleibt eine Gleichheit:
1 + sin x = 1 + sinx
- Übung 2
Lösen Sie die folgende trigonometrische Gleichung und geben Sie die Lösung für Werte zwischen 0 und 360º an:
tg x + sekzwei x = 3
Lösung
Im linken Begriff gibt es zwei trigonometrische Verhältnisse, daher ist es notwendig, alles auf ein einziges zu reduzieren, um das Unbekannte lösen zu können. Der Begriff sekzwei x wird durch eine der pythagoreischen Identitäten ausgedrückt:
sekzwei α = 1 + tgzwei α
Das Einsetzen in die Gleichung bleibt:
tg x + 1 + tgzwei x = 3
Neuordnung der Begriffe:
tgzwei x + tg x + 1 = 3
Diese Gleichung wird durch Ändern der Variablen gelöst:
tg x = u
oderzwei + u + 1 - 3 = 0 → uzwei + u - 2 = 0
Diese quadratische Gleichung lässt sich leicht durch Faktorisierung lösen:
(u + 2) (u-1) = 0
Deshalb u1 = -2 und uzwei = 1, was entspricht:
tg x1 = -2
tg xzwei = 1
Schließlich:
x1 = arctg (-2) = 296,6º
xzwei = arctg (1) = 45º
Verweise
- Carena, M. 2019. Voruniversitäres Mathematikhandbuch. Nationale Universität des Litoral.
- Figuera, J. 1999. Mathematics. 1. Diversifiziert. Bolivarian Collegiate Editions.
- Hoffman, J. Auswahl mathematischer Themen. Band 4.
- Jiménez, R. 2008. Algebra. Prentice Halle.
- Wikipedia. Trigonometrie-Identitäten und -Formeln. Wiederhergestellt von: es.wikipedia.org.
- Zapata, F. 4 Möglichkeiten, eine quadratische Gleichung zu lösen. Wiederhergestellt von: francesphysics.blogspot.com.
- Zill, D. 1984. Algebra und Trigonometrie. Mcgraw Hügel.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.