Das Homoskedastizität In einem prädiktiven statistischen Modell tritt es auf, wenn in allen Datengruppen einer oder mehrerer Beobachtungen die Varianz des Modells in Bezug auf die erklärenden (oder unabhängigen) Variablen konstant bleibt.
Ein Regressionsmodell kann homoskedastisch sein oder nicht. In diesem Fall sprechen wir von Heteroskedastizität.
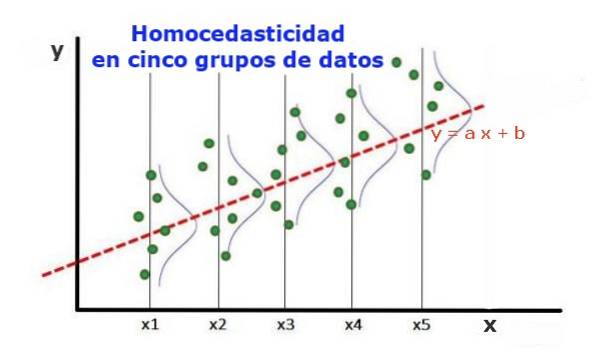
Ein statistisches Regressionsmodell mehrerer unabhängiger Variablen wird nur dann als homoskedastisch bezeichnet, wenn die Varianz des Fehlers der vorhergesagten Variablen (oder die Standardabweichung der abhängigen Variablen) für verschiedene Gruppenwerte der erklärenden oder unabhängigen Variablen einheitlich bleibt.
In den fünf Datengruppen in Abbildung 1 wurde die Varianz in jeder Gruppe in Bezug auf den durch die Regression geschätzten Wert berechnet, was dazu führt, dass sie in jeder Gruppe gleich ist. Es wird weiterhin angenommen, dass die Daten der Normalverteilung folgen.
Auf grafischer Ebene bedeutet dies, dass die Punkte gleichmäßig um den durch die Regressionsanpassung vorhergesagten Wert verteilt sind oder dass das Regressionsmodell den gleichen Fehler und die gleiche Gültigkeit für den Bereich der erklärenden Variablen aufweist..
Artikelverzeichnis
Um die Bedeutung der Homoskedastizität in der prädiktiven Statistik zu veranschaulichen, muss das entgegengesetzte Phänomen, die Heteroskedastizität, gegenübergestellt werden.
Im Fall von Abbildung 1, in der Homoskedastizität vorliegt, gilt Folgendes:
Var ((y1-Y1); X1) ≤ Var ((y2-Y2); X2) ≤ Var ((y4-Y4); X4)
Wo Var ((yi-Yi); Xi) die Varianz darstellt, repräsentiert das Paar (xi, yi) Daten aus Gruppe i, während Yi der Wert ist, der durch die Regression für den Mittelwert Xi der Gruppe vorhergesagt wird. Die Varianz der n Daten aus Gruppe i wird wie folgt berechnet:
Var ((yi-Yi); Xi) = ∑j (yij-Yi) ^ 2 / n
Im Gegenteil, wenn Heteroskedastizität auftritt, ist das Regressionsmodell möglicherweise nicht für die gesamte Region gültig, in der es berechnet wurde. Abbildung 2 zeigt ein Beispiel für diese Situation.
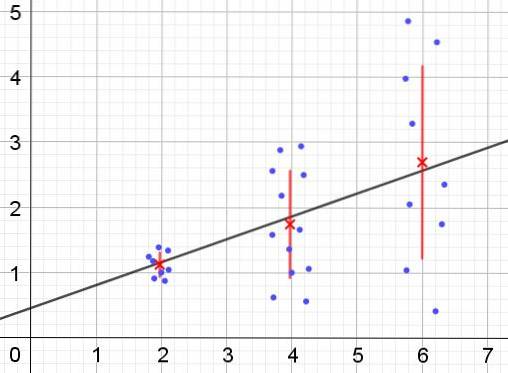
Abbildung 2 zeigt drei Datengruppen und die Anpassung des Satzes unter Verwendung einer linearen Regression. Es ist zu beachten, dass die Daten in der zweiten und dritten Gruppe stärker verteilt sind als in der ersten Gruppe. Die Grafik in Abbildung 2 zeigt auch den Mittelwert jeder Gruppe und ihren Fehlerbalken ± σ mit der σ-Standardabweichung jeder Datengruppe. Es ist zu beachten, dass die Standardabweichung σ die Quadratwurzel der Varianz ist.
Es ist klar, dass sich im Fall der Heteroskedastizität der Regressionsschätzungsfehler im Wertebereich der erklärenden oder unabhängigen Variablen ändert, und in den Intervallen, in denen dieser Fehler sehr groß ist, ist die Regressionsvorhersage unzuverlässig oder nicht anwendbar.
In einem Regressionsmodell müssen die Fehler oder Residuen (und -Y) mit gleicher Varianz (σ ^ 2) über das Werteintervall der unabhängigen Variablen verteilt werden. Aus diesem Grund muss ein gutes Regressionsmodell (linear oder nichtlinear) den Homoskedastizitätstest bestehen..
Die in Abbildung 3 gezeigten Punkte entsprechen den Daten einer Studie, in der nach einem Zusammenhang zwischen den Preisen (in Dollar) der Häuser in Abhängigkeit von der Größe oder Fläche in Quadratmetern gesucht wird.
Das erste zu testende Modell ist das einer linearen Regression. Zunächst wird angemerkt, dass der Bestimmungskoeffizient R ^ 2 der Anpassung ziemlich hoch ist (91%), so dass angenommen werden kann, dass die Anpassung zufriedenstellend ist..
Es können jedoch zwei Bereiche klar vom Anpassungsdiagramm unterschieden werden. Einer von ihnen, der rechts in einem Oval eingeschlossen, erfüllt Homoskedastizität, während der Bereich links keine Homoskedastizität aufweist.
Dies bedeutet, dass die Vorhersage des Regressionsmodells im Bereich zwischen 1800 m ^ 2 und 4800 m ^ 2 angemessen und zuverlässig ist, außerhalb dieser Region jedoch sehr unzureichend. In der heteroskedastischen Zone ist nicht nur der Fehler sehr groß, sondern die Daten scheinen auch einem anderen Trend zu folgen als dem vom linearen Regressionsmodell vorgeschlagenen..
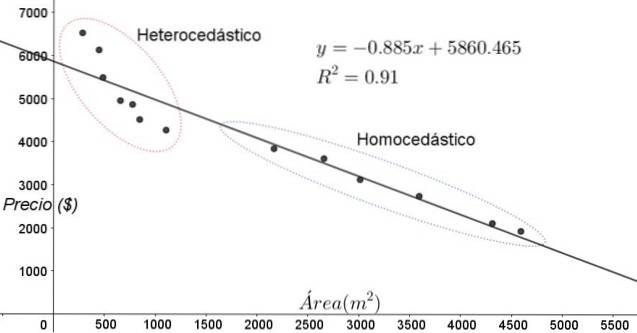
Das Streudiagramm der Daten ist der einfachste und visuellste Test für ihre Homoskedastizität. In Fällen, in denen es nicht so offensichtlich ist wie in dem in Abbildung 3 gezeigten Beispiel, ist es jedoch erforderlich, auf Diagramme mit Hilfsvariablen zurückzugreifen..
Um die Bereiche zu trennen, in denen Homoskedastizität erfüllt ist und in denen dies nicht der Fall ist, werden die standardisierten Variablen ZRes und ZPred eingeführt:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Es ist zu beachten, dass diese Variablen vom angewandten Regressionsmodell abhängen, da Y der Wert der Regressionsvorhersage ist. Unten ist das Streudiagramm ZRes gegen ZPred für dasselbe Beispiel:
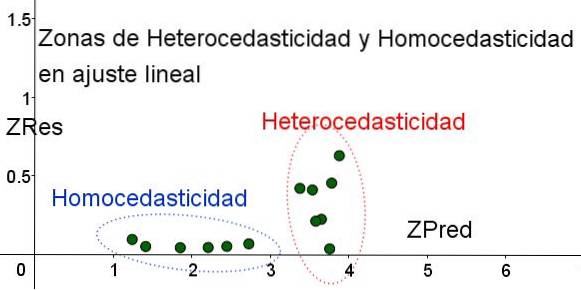
In der Grafik in Abbildung 4 mit den standardisierten Variablen ist der Bereich, in dem der Restfehler klein und gleichmäßig ist, klar von dem Bereich getrennt, in dem er nicht vorhanden ist. In der ersten Zone ist die Homoskedastizität erfüllt, während in dem Bereich, in dem der Restfehler sehr variabel und groß ist, die Heteroskedastizität erfüllt ist..
Die Regressionsanpassung wird auf dieselbe Datengruppe in Abbildung 3 angewendet. In diesem Fall ist die Anpassung nicht linear, da das verwendete Modell eine potenzielle Funktion enthält. Das Ergebnis ist in der folgenden Abbildung dargestellt:
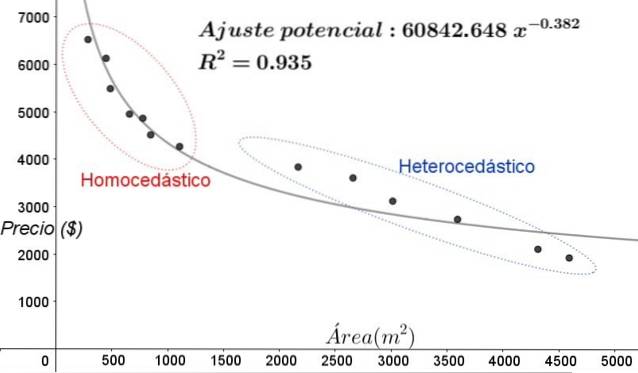
In der Grafik in Abbildung 5 sollten die homoskedastischen und heteroskedastischen Zonen deutlich angegeben werden. Es sollte auch beachtet werden, dass diese Zonen in Bezug auf diejenigen, die im linearen Anpassungsmodell gebildet wurden, vertauscht wurden.
In der Grafik von 5 ist ersichtlich, dass das Modell selbst bei einem ziemlich hohen Bestimmungskoeffizienten der Anpassung (93,5%) nicht für das gesamte Intervall der erklärenden Variablen geeignet ist, da die Daten für Werte größer als 2000 sind m ^ 2 weisen Heteroskedastizität auf.
Einer der am häufigsten verwendeten nichtgrafischen Tests, um zu überprüfen, ob die Homoskedastizität erfüllt ist oder nicht, ist der Breusch-Pagan-Test.
Nicht alle Details dieses Tests werden in diesem Artikel angegeben, aber seine grundlegenden Eigenschaften und die Schritte desselben werden in groben Zügen dargestellt:
Die meisten statistischen Softwarepakete wie SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic und einige andere enthalten den Homoskedastizitätstest von Breusch-Pagan. Ein weiterer Test zur Überprüfung der Gleichmäßigkeit der Varianz Levene-Test.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.