
Konstante Funktionsmerkmale, Beispiele, Übungen
Das konstante Funktion ist derjenige, bei dem der Wert von y konstant gehalten wird. Mit anderen Worten: Eine konstante Funktion hat immer die Form f (x) = k, wo k ist eine reelle Zahl.
Bei der grafischen Darstellung der Konstantenfunktion im Koordinatensystem xy, führt immer zu einer geraden Linie parallel zur horizontalen Achse oder Achse der x.
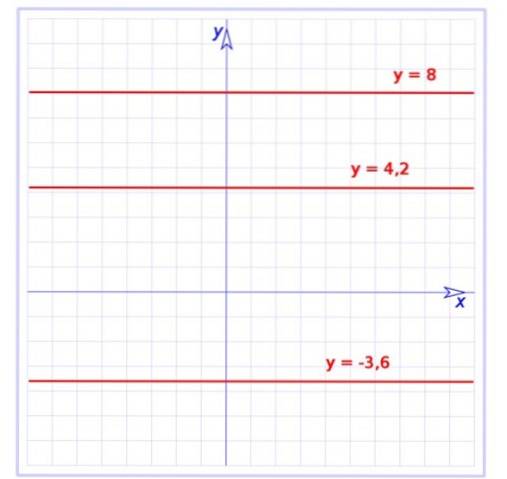
Diese Funktion ist ein besonderer Fall der affine Funktion, dessen Grafik ist auch eine gerade Linie, aber mit einer Steigung. Die konstante Funktion hat eine Steigung von Null, dh es handelt sich um eine horizontale Linie, wie in Abbildung 1 dargestellt.
Dort wird der Graph von drei konstanten Funktionen gezeigt:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Alle sind Linien parallel zur horizontalen Achse, die erste befindet sich unterhalb der Achse, während der Rest oberhalb der Achse liegt.
Artikelverzeichnis
- 1 Eigenschaften der konstanten Funktion
- 2 Beispiele
- 2.1 Eine andere Möglichkeit, eine konstante Funktion darzustellen
- 3 Gelöste Übungen
- 3.1 - Übung 1
- 3.2 - Übung 2
- 3.3 - Übung 3
- 3.4 - Übung 4
- 3.5 - Übung 6
- 4 Referenzen
Eigenschaften der konstanten Funktion
Wir können die Hauptmerkmale der konstanten Funktion wie folgt zusammenfassen:
-Das Diagramm ist eine gerade horizontale Linie.
-Es hat einen einzelnen Schnittpunkt mit der Achse Y., wert k.
-Ist kontinuierlich.
-Die Domäne der konstanten Funktion (die Menge der Werte, die die x) ist die Menge der reellen Zahlen R..
-Der Pfad, der Bereich oder die Gegendomäne (die Menge der Werte, die die Variable annimmt Y.) ist einfach die Konstante k.
Beispiele
Funktionen sind notwendig, um Verknüpfungen zwischen Größen herzustellen, die in irgendeiner Weise voneinander abhängen. Die Beziehung zwischen ihnen kann mathematisch modelliert werden, um herauszufinden, wie sich einer von ihnen verhält, wenn der andere variiert..
Dies hilft, Modelle für viele Situationen zu erstellen und Vorhersagen über deren Verhalten und Entwicklung zu treffen..
Trotz ihrer scheinbaren Einfachheit hat die konstante Funktion viele Anwendungen. Zum Beispiel, wenn es darum geht, Größen zu untersuchen, die über die Zeit oder zumindest für eine nennenswerte Zeit konstant bleiben.
Auf diese Weise verhalten sich Größen in Situationen wie den folgenden:
-Das Geschwindigkeit Kreuzfahrt mit einem Auto auf einer langen geraden Autobahn. Solange Sie nicht bremsen oder beschleunigen, hat das Auto eine gleichmäßige geradlinige Bewegung.

-Ein vollständig geladener Kondensator, der von einem Stromkreis getrennt ist, hat a Belastung zeitlich konstant.
-Schließlich unterhält ein Flatrate-Parkplatz eine Preis konstant, egal wie lange ein Auto dort geparkt ist.
Eine andere Möglichkeit, eine konstante Funktion darzustellen
Die konstante Funktion kann alternativ wie folgt dargestellt werden:
f (x) = kx0
Da jeder Wert von x erhöht auf 0 ergibt 1, der vorherige Ausdruck reduziert sich auf den bereits bekannten:
f (x) = k
Das passiert natürlich so lange wie der Wert von k unterscheidet sich von 0.
Deshalb wird die Konstantenfunktion auch als a klassifiziert Polynomfunktion vom Grad 0, da der Exponent der Variablen x ist 0.
Gelöste Übungen
- Übung 1
Beantworten Sie folgende Fragen:
a) Kann festgestellt werden, dass die durch x = 4 gegebene Linie eine konstante Funktion ist? Grund für Ihre Antwort.
b) Kann eine konstante Funktion einen x-Achsenabschnitt haben??
c) Ist die Funktion f (x) = w konstant?zwei?
Antwort auf
Hier ist der Graph der Linie x = 4:
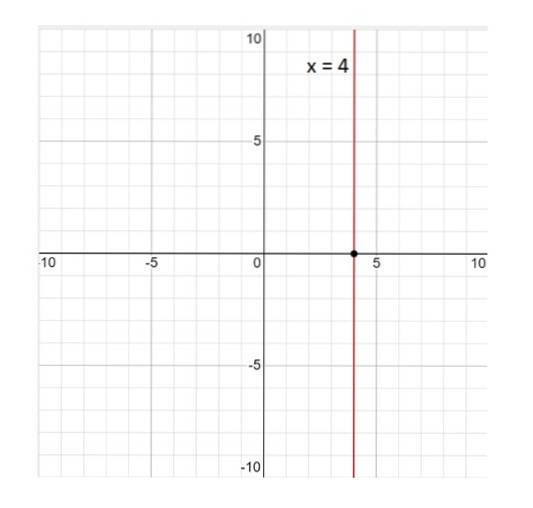
Die Linie x = 4 ist keine Funktion; per definitionem ist eine Funktion eine Beziehung, so dass bei jedem Wert der Variablen x entspricht einem einzelnen Wert von Y.. Und in diesem Fall ist dies nicht wahr, da der Wert x = 4 ist mit unendlichen Werten von verbunden Y.. Daher lautet die Antwort nein.
Antwort b
Im Allgemeinen hat eine konstante Funktion keinen Schnittpunkt mit der Achse x, es sei denn, es geht darum y = 0, In diesem Fall ist es die Achse x Richtig gesagt.
Antwort c
Ja seitdem w ist konstant, so ist sein Quadrat. Was zählt, ist das w hängen nicht von der Eingabevariablen ab x.
- Übung 2
Finden Sie den Schnittpunkt zwischen den Funktionen f (x) = 5 Y. g (x) = 5x - 2
Lösung
Um den Schnittpunkt zwischen diesen beiden Funktionen zu finden, können sie jeweils wie folgt umgeschrieben werden:
y = 5; y = 5x - 2
Sie werden ausgeglichen und erhalten:
5x - 2 = 5
Was ist eine lineare Gleichung ersten Grades, deren Lösung lautet:
5x = 5 + 2 = 7
x = 7/5
Der Schnittpunkt ist (7 / 5,5).
- Übung 3
Zeigen Sie, dass die Ableitung einer konstanten Funktion 0 ist.
Lösung
Aus der Definition des Derivats haben wir:

f (x + h) = k
Einsetzen in die Definition:

Auch wenn wir uns das Derivat als Änderungsrate vorstellen dy / dx, Die konstante Funktion ändert sich nicht, daher ist ihre Ableitung Null.
- Übung 4
Finden Sie das unbestimmte Integral von f (x) = k.
Lösung

Eine Mobilfunkgesellschaft bietet einen unbegrenzten Internet-Flatrate-Service für 15 US-Dollar pro Monat an. Was ist die Preisfunktion nach Zeit?
Lösung
Sei P der zu zahlende Preis in $ und t die Zeit, die in Tagen ausgedrückt werden kann. Die Funktion ist wie folgt eingestellt:
P (t) = 15
- Übung 6
Das folgende Diagramm der Geschwindigkeit gegen die Zeit entspricht der Bewegung eines Partikels.

Es fragt:
a) Schreiben Sie einen Ausdruck für die Geschwindigkeitsfunktion als Funktion der Zeit v (t).
b) Ermitteln Sie die vom Mobiltelefon zurückgelegte Entfernung im Zeitintervall zwischen 0 und 9 Sekunden.
Lösung für
Aus der gezeigten Grafik ist ersichtlich, dass:
-v = 2 m / s im Zeitintervall zwischen 0 und 3 Sekunden
-Das Mobiltelefon wird zwischen 3 und 5 Sekunden angehalten, da in diesem Intervall die Geschwindigkeit 0 ist.
-v = - 3 m / s zwischen 5 und 9 Sekunden.
Dies ist ein Beispiel für eine stückweise Funktion oder eine stückweise Funktion, die sich wiederum aus konstanten Funktionen zusammensetzt und nur für die angegebenen Zeitintervalle gültig ist. Es wird gefolgert, dass die gesuchte Funktion ist:

Lösung b
Aus dem v (t) -Diagramm kann die vom Mobiltelefon zurückgelegte Entfernung berechnet werden, die numerisch der Fläche unter / auf der Kurve entspricht. Auf diese Weise:
-Zurückgelegte Strecke zwischen 0 und 3 Sekunden = 2 m / s. 3 s = 6 m
-Zwischen 3 und 5 Sekunden wurde er angehalten, deshalb legte er keine Strecke zurück.
-Zurückgelegte Strecke zwischen 5 und 9 Sekunden = 3 m / s. 4 s = 12 m
Insgesamt legte das Handy 18 m zurück. Beachten Sie, dass die zurückgelegte Strecke positiv ist, obwohl die Geschwindigkeit im Intervall zwischen 5 und 9 Sekunden negativ ist. Was passiert ist, dass während dieses Zeitintervalls das Handy das Gefühl seiner Geschwindigkeit geändert hat.
Verweise
- Geogebra. Konstante Funktionen. Wiederhergestellt von: geogebra.org.
- Maplesoft. Die konstante Funktion. Wiederhergestellt von: maplesoft.com.
- Wikibooks. Berechnung in einer Variablen / Funktionen / Konstantenfunktion. Wiederhergestellt von: es.wikibooks.org.
- Wikipedia. Konstante Funktion. Wiederhergestellt von: en.wikipedia.org
- Wikipedia. Konstante Funktion. Wiederhergestellt von: es.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.