
Resultierende Kraft, wie es berechnet und Übungen gelöst werden
Das Macht resultierend Es ist die Summe aller Kräfte, die auf denselben Körper wirken. Wenn ein Körper oder Gegenstand gleichzeitig mehreren Kräften ausgesetzt ist, tritt ein Effekt auf. Betätigungskräfte können durch eine einzige Kraft ersetzt werden, die den gleichen Effekt erzeugt. Diese einzelne Kraft ist die resultierende Kraft, die auch als Nettokraft bezeichnet wird und durch das Symbol dargestellt wird F.R. .
Der Effekt, den es erzeugt F.R. es wird von seiner Größe, Richtung und Sinn abhängen. Physikalische Größen, die Richtung und Sinn haben, sind Vektorgrößen.
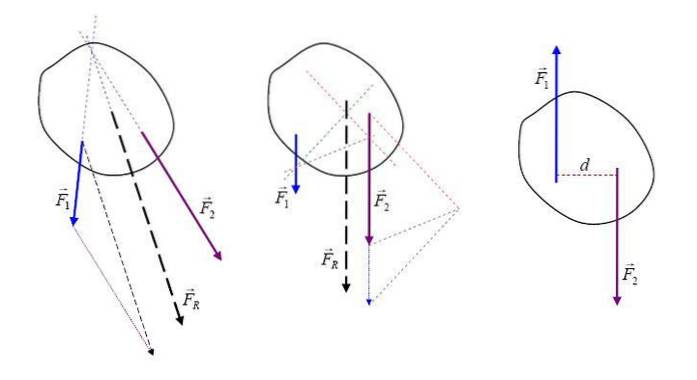
Als die auf einen Körpervektor einwirkenden Kräfte ist die resultierende Kraft F.R. ist eine Vektorsumme aller Kräfte und kann grafisch mit einem Pfeil dargestellt werden, der seine Richtung und Richtung angibt.
Mit der resultierenden Kraft wird das Problem eines Körpers, der von mehreren Kräften betroffen ist, vereinfacht, indem er auf eine einzige wirkende Kraft reduziert wird.
Artikelverzeichnis
- 1 Formel
- 2 Wie berechnet man die resultierende Kraft??
- 2.1 resultierend aus parallelen Kräften
- 2.2 Nicht parallele Kräfte
- 3 Gelöste Übungen
- 4 Referenzen
Formel
Die mathematische Darstellung der resultierenden Kraft ist eine Vektorsummation der Kräfte.
F.R.= ∑F. (1)
∑F = F.1+ F.zwei+ F.3+... F.N. (zwei)
F.R.= Resultierende Kraft
∑F = Summe der Kräfte
N.= Anzahl der Kräfte
Die resultierende Kraft kann auch durch die Newtonsche Gleichung des zweiten Gesetzes dargestellt werden.
F.R.= m.zu (3)
m= Körpermasse
a = Körperbeschleunigung
Wenn Gleichung (1) in Gleichung (3) eingesetzt wird, werden die folgenden Gleichungen erhalten:
∑F. = m.zu (4)
F.1+ F.zwei+ F.3+... F.N = m.zu (5)
Die mathematischen Ausdrücke (4) und (5) liefern Informationen über den Zustand des Körpers, indem sie den Beschleunigungsvektor erhalten zu.
Wie berechnet man die resultierende Kraft??
Die resultierende Kraft wird durch Anwendung des zweiten Newtonschen Gesetzes erhalten, das Folgendes besagt:
Die auf einen Körper wirkende Nettokraft ist gleich dem Produkt seiner Masse und der Beschleunigung, die er erhält. (Gleichung (3))
Die Beschleunigung des Körpers hat die Richtung der ausgeübten Nettokraft. Wenn alle auf den Körper einwirkenden Kräfte bekannt sind, würde es ausreichen, ihn vektoriell zu addieren, um die resultierende Kraft zu erhalten. Wenn die resultierende Kraft bekannt ist, würde es ebenfalls ausreichen, sie durch die Masse des Körpers zu teilen, um ihre Beschleunigung zu erhalten.
Wenn die resultierende Kraft Null ist, befindet sich der Körper in Ruhe oder mit konstanter Geschwindigkeit. Wenn eine einzelne Kraft auf den Körper wirkt, ist die resultierende Kraft gleich dieser Kraft F.R.=F..
Wenn mehrere Kräfte auf denselben Körper wirken, müssen die Vektorkomponenten der Kraft berücksichtigt werden und ob diese Kräfte parallel sind oder nicht.
Wenn wir beispielsweise ein Buch horizontal auf einen Tisch schieben, sind die Kräfte in horizontaler Richtung die einzigen, die den Körper beschleunigen. Die vertikale Nettokraft auf das Buch ist Null.
Wenn die auf das Buch ausgeübte Kraft eine Neigung in Bezug auf die horizontale Ebene des Tisches aufweist, wird die Kraft als Funktion der vertikalen und horizontalen Komponenten geschrieben.
Ergebnis parallele Kräfte
Die parallelen Kräfte, die auf einen Körper wirken, sind diejenigen Kräfte, die in die gleiche Richtung wirken. Sie können zwei Arten von gleichem oder entgegengesetztem Sinn sein.
Wenn die auf einen Körper einwirkenden Kräfte dieselbe Richtung und dieselbe Richtung haben oder in die entgegengesetzte Richtung weisen, wird die resultierende Kraft erhalten, indem die algebraische Summe der numerischen Werte der Kräfte ausgeführt wird.
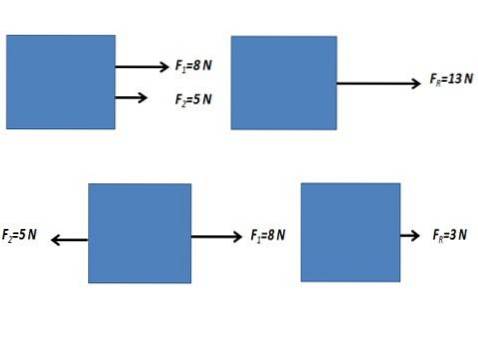
Nicht parallele Kräfte
Wenn nicht parallele Kräfte auf einen Körper ausgeübt werden, hat das Ergebnis der Kräfte rechteckige und vertikale Komponenten. Der mathematische Ausdruck zur Berechnung der Nettokraft lautet:
F.R.zwei= ((∑ F.x)zwei+((∑ F.Y.)zwei (6)
so θx= ∑ F.Y. / ∑ F.x (7)
∑ F.x und ∑ F.x= Algebraische Summation der Komponenten x und Y. der angewendeten Kräfte
θx= Winkel, der durch die resultierende Kraft gebildet wird F.R. mit Welle x
Beachten Sie, dass die resultierende Ausdruckskraft (6) nicht fett hervorgehoben ist und nur den numerischen Wert ausdrückt. Die Richtung wird durch den Winkel bestimmt θx.
Ausdruck (6) gilt für Kräfte, die in derselben Ebene wirken. Wenn Kräfte im Raum wirken, wird die Komponente berücksichtigt z Kraft beim Arbeiten mit rechteckigen Bauteilen.
Gelöste Übungen
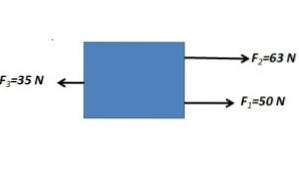
Die parallelen Kräfte in derselben Richtung werden addiert und subtrahiert mit der parallelen Kraft in entgegengesetzter Richtung
F.R.= 63 N + 50 N - 35 N = 78 N.
Die resultierende Kraft hat eine Größe von 78 N in horizontaler Richtung.
2. Berechnen Sie die resultierende Kraft eines Körpers unter dem Einfluss zweier Kräfte F.1 Y. F.zwei. Die Kraft F.1 es hat eine Stärke von 70N und wird horizontal angewendet. Die Kraft F.zwei hat eine Größe von 40 N und wird in einem Winkel von 30 ° zur horizontalen Ebene angewendet.
Um diese Übung zu lösen, wird ein Freikörperdiagramm mit den Koordinatenachsen gezeichnet x und Y.
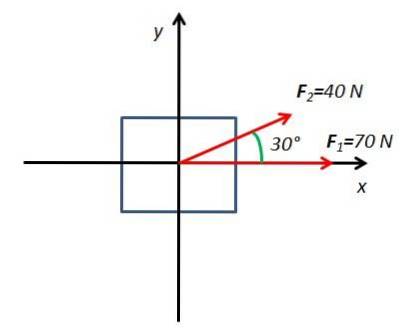
Alle Komponenten sind bestimmt x und Y. der auf den Körper einwirkenden Kräfte. Die Kraft F.1 hat nur eine horizontale Komponente auf der Achse x. Die Kraft F.zwei Es besteht aus zwei Komponenten F.2x und F.2 und die aus den Sinus- und Cosinusfunktionen des Winkels 30 ° erhalten werden.
F.1x = F.1=70N
F.2x = F.zwei cos 30 ° = 40 N.cos 30 ° = 34,64 N.
F.1y = 0
F.2 und= F.zwei ohne 30 ° = 40 ohne 30 ° = 20N
∑ F.x =70 N + 34,64 N = 104,64 N.
∑ F.Y.=20N + 0 = 20N
Sobald die resultierenden Kräfte in der Welle bestimmt wurden x und Y. Wir fahren fort, um den numerischen Wert der resultierenden Kraft zu erhalten.
F.R.zwei= ((∑ F.x)zwei+((∑ F.Y.)zwei
Die resultierende Kraft ist die Quadratwurzel der Summe der quadratischen Komponenten der Kräfte
F.R.= √ (104,64 N)zwei+(20N)zwei
F.R.= 106,53N
Der Winkel, der durch die resultierende Kraft gebildet wird F.R. wird aus dem folgenden Ausdruck erhalten:
θx= so-1((∑ F.Y. / ∑ F.x)
θx= so-1(20N /. 104,64 N) = 10,82 °
Die resultierende Kraft F.R. hat eine Größe von 106,53 N und eine Richtung, die durch den Winkel von 10,82 ° bestimmt wird, den es mit der Horizontalen bildet.
Verweise
- Dola, G, Duffy, M und Percival, A.. Physik. Spanien: Heinemann, 2003.
- Avison, J H.. Die Welt der Physik. Indien: Thomas Nelson and Sons, 1989.
- Pinsent, M.. Physikalische Prozesse. Vereinigtes Königreich: Nelson Thomas, 2002.
- Yadav, S K.. Technische Mechanik. Delhi: Discovery Publishing House, 2006.
- Serway, R A und Jewett, J W.. Physik für Wissenschaftler und Ingenieure. Kalifornien, USA: Brooks / Cole, 2010.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.