
Zufälliges Experimentkonzept, Probenraum, Beispiele
Es ist die Rede von zufälliges Experiment wenn das Ergebnis jedes einzelnen Versuchs nicht vorhersehbar ist, obwohl die Wahrscheinlichkeit des Auftretens eines bestimmten Ergebnisses ermittelt werden kann.
Es sollte jedoch klargestellt werden, dass es nicht möglich ist, das gleiche Ergebnis eines Zufallssystems mit den gleichen Parametern und Anfangsbedingungen in jedem Versuch des Experiments zu reproduzieren..

Ein gutes Beispiel für ein zufälliges Experiment ist das Würfeln. Selbst wenn darauf geachtet wird, den Würfel auf die gleiche Weise zu würfeln, führt jeder Versuch zu einem unvorhersehbaren Ergebnis. Das einzige, was gesagt werden kann, ist, dass das Ergebnis eines der folgenden sein kann: 1, 2, 3, 4, 5 oder 6.
Das Werfen einer Münze ist ein weiteres Beispiel für ein zufälliges Experiment mit nur zwei möglichen Ergebnissen: Kopf oder Zahl. Obwohl die Münze aus derselben Höhe und auf dieselbe Weise geworfen wird, ist der Zufallsfaktor immer vorhanden, was bei jedem neuen Versuch zu Unsicherheit führt..
Das Gegenteil eines zufälligen Experiments ist ein deterministisches Experiment. Beispielsweise ist bekannt, dass jedes Mal, wenn Wasser auf Meereshöhe gekocht wird, die Siedetemperatur 100 ºC beträgt. Es kommt jedoch nie vor, dass unter den gleichen Bedingungen das Ergebnis manchmal 90 ° C, andere 12 ° C und manchmal 100 ° C beträgt..
Artikelverzeichnis
- 1 Probenraum
- 1.1 Ereignis oder Ereignis
- 2 Beispiele
- 2.1 Beispiel 1
- 2.2 Beispiel 2
- 3 Referenzen
Probenraum
Die Menge aller möglichen Ergebnisse eines zufälligen Experiments wird aufgerufen Probenraum. In dem zufälligen Experiment des Würfelns eines Würfels beträgt der Probenraum:
D = 1, 2, 3, 4, 5, 6.
Auf der anderen Seite ist der Wurfraum beim Werfen einer Münze:
M = Köpfe, Stempel.
Ereignis oder Vorkommen
In einem zufälligen Experiment a Veranstaltung es ist das Auftreten oder Nichtvorhandensein eines bestimmten Ergebnisses. Zum Beispiel ist im Fall eines Münzwurfs ein Ereignis oder ein Ereignis, dass es Köpfe hochkommt.
Ein anderes Ereignis in einem zufälligen Experiment könnte das folgende sein: dass eine Zahl kleiner oder gleich drei auf dem Würfelwurf gewürfelt wird.
Wenn das Ereignis eintritt, ist die Menge der möglichen Ergebnisse die Menge:
E = 1, 2, 3
Dies ist wiederum eine Teilmenge des Probenraums oder der Probenmenge:
M = 1, 2, 3, 4, 5, 6.
Beispiele
Hier sind einige Beispiele, die das Obige veranschaulichen:
Beispiel 1
Angenommen, zwei Münzen werden nacheinander geworfen. Es fragt:
a) Geben Sie an, ob es sich um ein zufälliges Experiment oder im Gegenteil um ein deterministisches Experiment handelt.
b) Wie groß ist der Probenraum S dieses Experiments??
c) Geben Sie die Menge von Ereignis A an, die der Tatsache entspricht, dass das Experiment zu Kopf und Zahl führt.
d) Berechnen Sie die Wahrscheinlichkeit, dass Ereignis A auftritt.
e) Finden Sie schließlich die Wahrscheinlichkeit, dass Ereignis B eintritt: Im Ergebnis erscheinen keine Köpfe.
Lösung
a) Es ist ein zufälliges Experiment, da es keine Möglichkeit gibt, vorherzusagen, was das Ergebnis eines Wurfs der beiden Münzen sein wird.
b) Der Probenraum ist die Menge aller möglichen Ergebnisse:
S = (c, c), (c, s), (s, c), (s, s)
c) Ereignis A kann, falls es auftritt, die folgenden Ergebnisse haben:
A = (c, s), (s, c)
d) Die Wahrscheinlichkeit, dass Ereignis A auftritt, wird erhalten, indem die Anzahl der Elemente der Menge A durch die Anzahl der Elemente der Menge S dividiert wird, die dem Probenraum entsprechen:
P (A) = 2/4 = ½ = 0,5 = 50%
e) Die Menge möglicher Ergebnisse, die Ereignis B entsprechen (im Ergebnis erscheinen keine Köpfe), ist:
B = (s, s)
Daher ist die Wahrscheinlichkeit, dass Ereignis B in einem Versuch auftritt, der Quotient zwischen der Anzahl der möglichen Ergebnisse von B und der Anzahl der Gesamtfälle:
P (B) = ¼ = 0,25 = 25%.
Beispiel 2
Eine Tasche enthält 10 weiße und 10 schwarze Murmeln. Drei Murmeln werden nacheinander zufällig und ohne nach innen zu schauen aus dem Beutel genommen.
a) Bestimmen Sie den Probenraum dieses zufälligen Experiments.
b) Bestimmen Sie den Satz von Ergebnissen, die dem Ereignis A entsprechen, das darin besteht, nach dem Experiment zwei schwarze Murmeln zu haben.
c) Ereignis B soll mindestens zwei schwarze Murmeln erhalten, die Menge B der Ergebnisse für dieses Ereignis bestimmen.
d) Wie hoch ist die Wahrscheinlichkeit, dass Ereignis A eintritt??
e) Bestimmen Sie die Wahrscheinlichkeit, dass Ereignis B auftritt.
f) Bestimmen Sie die Wahrscheinlichkeit, dass das Ergebnis des Zufallsexperiments ist, dass Sie mindestens einen schwarzen Marmor haben. Dieses Ereignis heißt C..

Lösung für
Um den Probenraum zu konstruieren, ist es nützlich, ein Baumdiagramm wie das in Abbildung 3 gezeigte zu erstellen:
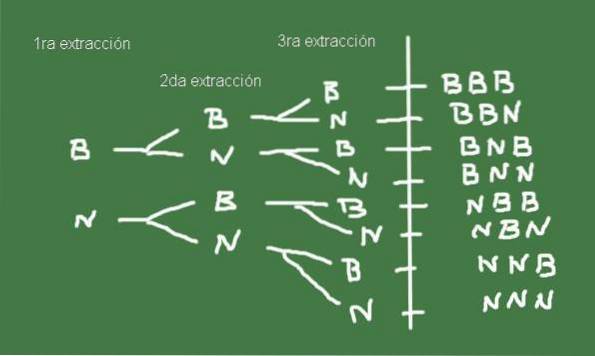
Die Menge Ω möglicher Ergebnisse beim Extrahieren von drei Murmeln aus einem Beutel mit der gleichen Anzahl schwarzer und weißer Murmeln ist genau der Probenraum dieses zufälligen Experiments.
Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)
Lösung b
Die Menge der möglichen Ergebnisse, die dem Ereignis A entsprechen, das aus zwei schwarzen Murmeln besteht, ist:
A = (b, n, n), (n, b, n), (n, n, b)
Lösung c
Ereignis B ist definiert als: „mindestens zwei schwarze Murmeln haben, nachdem drei davon zufällig gezogen wurden“. Die Menge der möglichen Ergebnisse für Ereignis B ist:
B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)
Lösung d
Die Wahrscheinlichkeit, Ereignis A zu haben, ist der Quotient zwischen der Anzahl möglicher Ergebnisse für dieses Ereignis und der Gesamtzahl möglicher Ergebnisse, dh der Anzahl von Elementen im Probenraum.
P (A) = n (A) / n (Ω) = 3/8 = 0,375 = 37,5%
Es besteht also eine 37,5% ige Chance, zwei schwarze Murmeln zu haben, nachdem drei Murmeln zufällig aus der Tasche gezogen wurden. Beachten Sie jedoch, dass wir das genaue Ergebnis des Experiments in keiner Weise vorhersagen können.
Lösung e
Die Wahrscheinlichkeit, dass Ereignis B eintritt, das darin besteht, mindestens einen schwarzen Marmor zu erhalten, ist:
P (B) = n (B) / n (Ω) = 4/8 = 0,5 = 50%
Dies bedeutet, dass die Möglichkeit, dass Ereignis B auftritt, gleich der Wahrscheinlichkeit ist, dass es nicht auftritt.
Lösung f
Die Wahrscheinlichkeit, nach dem Extrahieren von drei davon mindestens einen schwarzen Marmor zu erhalten, ist gleich 1 minus der Wahrscheinlichkeit, dass das Ergebnis "die drei weißen Murmeln" sind..
P (C) = 1 - P (b b b) = 1 - ⅛ = ⅞ = 0,875 = 87,5%
Jetzt können wir dieses Ergebnis überprüfen und feststellen, dass die Anzahl der Möglichkeiten, mit denen das Ereignis C auftritt, gleich der Anzahl der Elemente der möglichen Ergebnisse für das Ereignis C ist:
C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)
n (C) = 7
P (C) = n (C) / n (Ω) = ⅞ = 87,5%
Verweise
- CanalPhi. Zufälliges Experiment. Wiederhergestellt von: youtube.com.
- MateMovil. Zufälliges Experiment. Wiederhergestellt von: youtube.com
- Pishro Nick H. Einführung in die Wahrscheinlichkeit. Wiederhergestellt von: Wahrscheinlichkeitskurs.com
- Ross. Wahrscheinlichkeit und Statistik für Ingenieure. Mc-Graw Hill.
- Wikipedia. Experiment (Wahrscheinlichkeitstheorie). Wiederhergestellt von: en.wikipedia.com
- Wikipedia. Deterministisches Ereignis. Wiederhergestellt von: es. wikipedia.com
- Wikipedia. Zufälliges Experiment. Wiederhergestellt von: es.wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.